Functions of Several Variables
Introduction
It is a good idea to review the basic notion of functions. This website contains an introductory text on functions.
Recall that the definition of Cartesian product of sets (from the text introductory text on sets) allows us to write \(\mathbb R^2\) for the set of all ordered pairs \((x,y)\) where \(x\) and \(y\) are real numbers. Elements of \(\mathbb R^2\) are \((1,3)\), \((-6,-3)\), and many others. It is very important to be clear on the fact that \(1\not\in \mathbb R^2\) as \(1\) itself is not an ordered pair.
In multivariable calculus we will often consider functions \(f:\mathbb R^2\to\mathbb R\) and call them functions of two variables. Similarly, any function \(f:A\to B\) where \(A\subseteq R^2\) will be called a function of two variables, and any function of the form \(f:A\to\mathbb R\) with \(A\subseteq \mathbb R^3\) will be called a function of three variables. Likewise, a function \(f:A\to\mathbb R\) where \(A\subseteq \mathbb R^n\) will be called a function of \(n\) variables.
An example of a function of two variables is \(f(x,y)=9+\sin(x+y^2)-\cos(xy)+e^{x\cdot(\sin x+y)}\). This is one of the function we’ll probably never study as it is too complicated, but you got the idea.
Graphs of functions
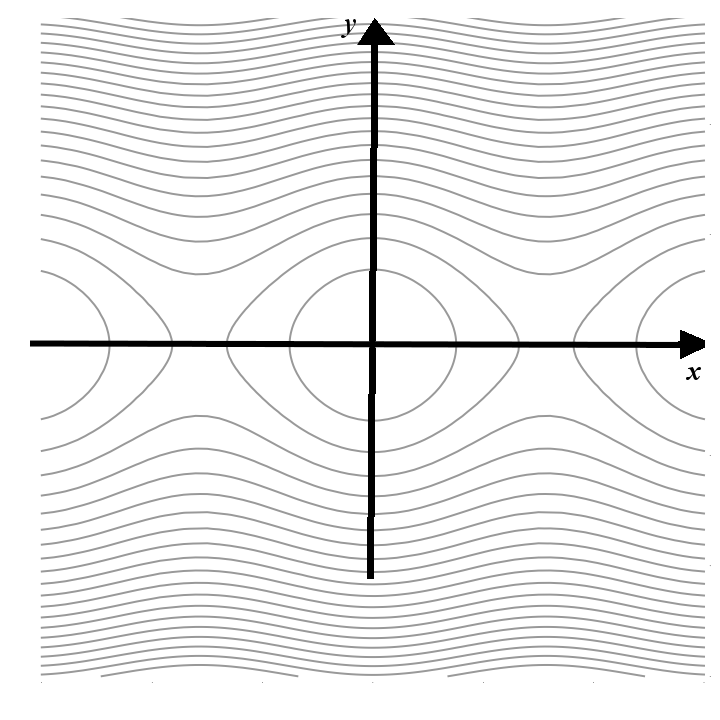
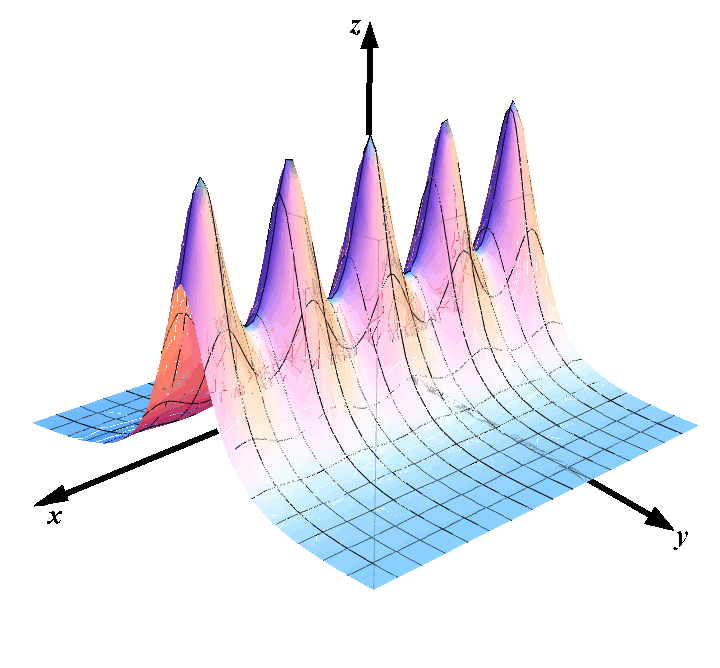
If \(f:\mathbb R^2\to\mathbb R\) is a function of two variables, its graph is the set in \(\mathbb R^3\) consisting of all points \((x,y,z)\) such that \(z=f(x,y)\). Consider, for example, the function \[f(x,y)=\frac{9}{1+\sin^2 x+y^2}.\] The points on its graph are colored and shown in the picture below:
Level curves
The concept of level curves comes from geography where people use two-dimensional maps to draw the three dimensional terrain. This is done through a series of optical illusions. Geographers plot contour lines that connect points of the same altitude. These contours are called level curves. Then they use some colors, but we are not interested in that.
In mathematics, the concept of level curves has to be formally defined. We start by assuming that we are given a surface. We assume that the surface is defined as the graph of a function \(z=f(x,y)\). For each constant \(c\in\mathbb R\), the intersection of the plane \(z=1\) with the surface \(z=f(x,y)\) is a curve whose \(x\) and \(y\) coordinates satisfy the equation \(f(x,y)=c\).
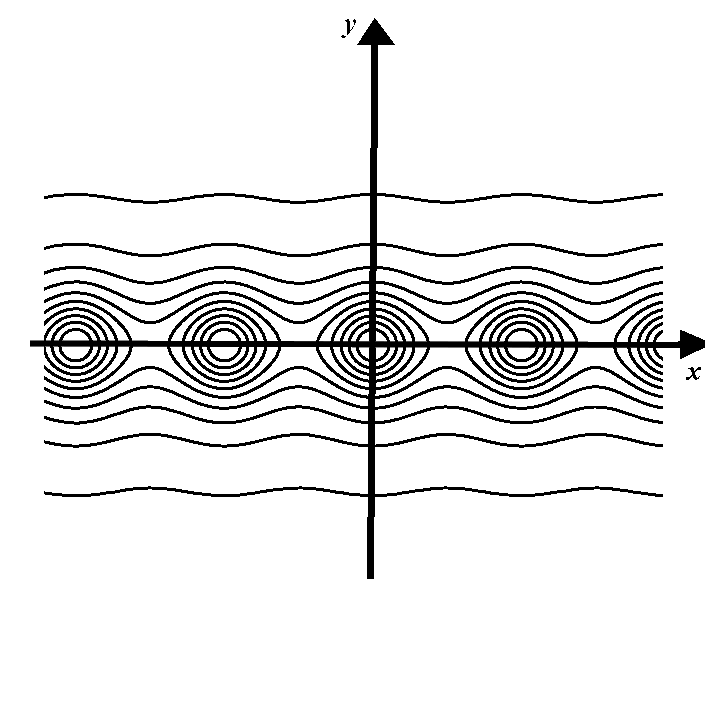
For the function \(\displaystyle f(x,y)=\frac{9}{1+\sin^2 x+y^2}\), the level sets are shown in the picture below.
Practice problems
(A) \(f(g(3,4), g(4,3))\) \(\quad\quad\) (B) \(f(g(-3,3))\) \(\quad\quad\) (C) \(g(f(3,5))\) \(\quad\quad\) (D) \(f(g(1,2),3,4)\) \(\quad\quad\) (E) \(g(f(9))\)
- (A) Empty set.
- (B) Entire \(\mathbb R^2\).
- (C) All the points that do not belong to the parabolas \(x=3y^2\) and \(x=3y^2+3\).
- (D) All the points to the left of the parabola \(x=3y^2\).
- (E) All the points to the right of the parabola \(x= 3y^2\) that do not belong to the parabola \(x=3y^2+3\).
- (A)
- (B)
- (C)
- (D)

- (E)