Tangent Planes
Tangent planes to graphs of functions
Assume that \(f(x,y)\) is a function of two variables. Its graph is a surface \(z=f(x,y)\). Our goal is to find an equation of the tangent plane passing trough a point \(A(x_0,y_0,z_0)\) on the surface.
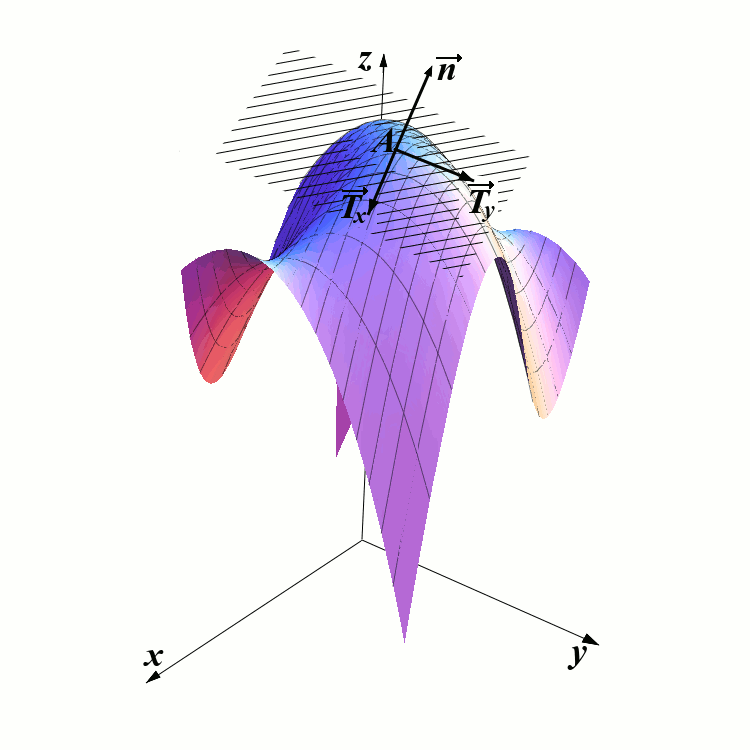
In the picture above, you can see a graph of a surface \(z=f(x,y)\) and a point \(A\) on that graph. Our goal is to find the equation of the shaded plane. In order to do this, we just need to find the coordinates of the normal vector \(\overrightarrow{n}\).
Recall that in the single variable calculus, the quantity \(f^{\prime}(a)\) represented the slope of the tangent line to the graph of \(f\) at the point \(a\). The tangent vector is then equal to \(\overrightarrow T=\langle 1, f^{\prime}(a)\rangle\).
There are many tangent vectors, because if we have one, by increasing or decreasing its length we may get a lot of them. Here, the vector \(\langle 1, f^{\prime}(a)\rangle\) is one of them, because its slope is \(f^{\prime}(a)\).
In multivariable calculus, the tangent to the surface is a plane, rather than a vector. The quantity \(f_x(x_0,y_0,z_0)\) also represents a slope of a certain vector. This vector belongs to the tangent plane, and is parallel to the \(xz\) plane. Let us call this vector \(\overrightarrow T_x\). Let us find its coordinates, i.e. let us find real numbers \(p\), \(q\), and \(r\) such that \[\overrightarrow T_x=\langle p,q,r\rangle.\]
First of all \(q\) is easy to find. It is equal to \(0\). The coordinates \(p\) and \(r\) are obtained in the same way as in single-variable calculus. We may take \(p=1\) and \(r=f_x(x_0,y_0)\). Therefore we have \[\overrightarrow T_x(x_0,y_0)=\langle 1,0,f_x(x_0,y_0)\rangle.\] Similarly, we obtain another vector that belongs to the tangent plane: \[\overrightarrow T_y(x_0,y_0)=\langle 0,1,f_y(x_0,y_0)\rangle.\]
And now we use a magnificent trick: Normal vector can be obtained as a cross product of \(\overrightarrow T_x\) and \(\overrightarrow T_y\). Thus:
\[\overrightarrow n(x_0,y_0)=
\overrightarrow T_x\times\overrightarrow T_y=\left|\begin{array}{ccc} \overrightarrow i& \overrightarrow j & \overrightarrow k \newline 1 & 0 & f_x \newline 0 & 1 & f_y \end{array}\right|=\langle -f_x,-f_y,1\rangle.
\]
We have obtained the following theorem:
The Equation of the Tangent Plane
If a surface is defined as a graph of \(z=f(x,y)\), and if \(A(x_0,y_0,z_0)\) is a point on the surface, then a normal vector to the tangent plane at the point \(A\) is given by \[\overrightarrow n(x_0,y_0)=\langle -f_x(x_0,y_0), -f_y(x_0,y_0),1\rangle.\]
The equation of the plane tangent to the surface at the point \(A\) is given by:
\[-f_x(x_0,y_0)(x-x_0)-f_y(x_0,y_0)(y-y_0)+(z-z_0)=0.\]
Example 1 Consider the function: \[f(x,y)=3-x^2-y^2-3x^3y+2xy.\] Find the equation of the tangent plane to the surface at the point \(M(0,1,2)\).
From \(f_x(x,y)=-2x-9x^2y+2y\) and \(f_y(x,y)=-2y+2x^3+2x\) we obtain \(f_x(0,1)=2\) and \(f_y(0,1)=-2\). Therefore \(\overrightarrow n(0,1)=\langle -2,2,1\rangle\) and the equation of the tangent plane is: \[-2x+2(y-1)+z-2=0.\]
Example 2 Find the equation of the tangent plane to the ellipsoid \(x^2+4y^2+9z^2=1\) at the point \(\left(\frac12,\frac14,\frac{\sqrt 2}3\right)\).
The graph of the function \(z=\frac19\sqrt{1-x^2-4y^2}\) is the top part of the ellipsoid. The point \(\left(\frac12,\frac14,\frac{\sqrt 2}3\right)\) belongs to the top part (since \(z\geq 0\)). We have \(z_x(x,y)=-\frac{x}{3\sqrt{1-x^2-4y^2}}\) and \(z_y(x,y)=-\frac{4y}{3\sqrt{1-x^2-4y^2}}\). We thus have \(z_x\left(\frac12,\frac14\right)=-\frac{\sqrt 2}6\) and \(z_y\left(\frac12,\frac14\right)=-\frac{\sqrt 2}3\). Therefore
\begin{eqnarray*}
\overrightarrow N(x,y)&=&\langle -z_x,-z_y,1\rangle=\left\langle \frac{\sqrt 2}6,\frac{\sqrt 2}3,1\right\rangle,
\end{eqnarray*}
and the equation of the tangent plane is
\[\frac{\sqrt 2}6\left(x-\frac12\right)+\frac{\sqrt 2}3\left(y-\frac14\right)+\left(z-\frac{\sqrt 2}3\right)=0.\]
Tangent planes to surfaces given by parametric equations
Assume that the surface \(S\) is given by its parametric equations:
\begin{eqnarray*}
x&=& X(s,t)\\
y&=& Y(s,t)\\
z&=&Z(s,t),
\end{eqnarray*}
where \(X\), \(Y\), and \(Z\) are differentiable functions of two variables. Assume that we want to find the tangent plane to the surface \(S\) at the point \((x_0,y_0,z_0)\). Since each point of \(S\) is obtained when a particular pair \((s,t)\) is plugged into the equations above, we may assume that there exists a pair \((x_0,y_0)\) such that \((x_0,y_0,z_0)=(X(s_0,t_0),Y(s_0,t_0),Z(s_0,t_0))\).
Consider the function \(\overrightarrow R(s,t)=\langle X(s,t), Y(s,t), Z(s,t)\rangle\).
Theorem
The normal vector to the tangent plane of \(S\) at the point \((x_0,y_0,z_0)\) is parallel to the vector \[\overrightarrow N_0= \frac{\partial }{\partial s}\overrightarrow R(s_0,t_0)\times \frac{\partial }{\partial t}\overrightarrow R(s_0,t_0).\]
If we fix \(t=t_0\), then the function \(\overrightarrow \gamma(s)=\overrightarrow R(s,t_0)\) determines the curve that is fully contained on the surface \(S\).
The vector \(\frac{d }{ds}\overrightarrow \gamma(s_0)\) is tangent vector to the curve \(\overrightarrow \gamma\) and hence to the surface \(S\). Notice that \(\frac{d }{ds}\overrightarrow \gamma(s_0)= \frac{\partial }{\partial s}\overrightarrow R(s_0,t_0)\) which means that \( \frac{\partial }{\partial s}\overrightarrow R(s_0,t_0)\) is a tangent vector to \(S\).
Similarly, the vector \( \frac{\partial }{\partial t}\overrightarrow R(s_0,t_0)\) is another tangent vector to \(S\), and these two vectors determine the tangent plane. Therefore, their cross product is parallel to the normal vector.
We will now solve the same problem as in Example 2 by parametrizing the ellipsoid.
Example 3
Find the equation of the plane tangent to the ellipsoid \(x^2+4y^2+9z^2=1\)
at the point \(\left(\frac12,\frac14,\frac{\sqrt 2}3\right)\).
The parametrization of the ellipsoid is:
\begin{eqnarray*}
x&=&\cos\theta\sin\phi\\
y&=&\frac12\sin\theta\sin\phi\\
z&=&\frac13\cos\phi\\
0\leq &\theta&\leq 2\pi\\
0\leq &\phi&\leq \pi.
\end{eqnarray*}
Notice that \((x,y,z)\left(\frac{\pi}4,\frac{\pi}4\right)=\left(\frac12,\frac14,\frac{\sqrt 2}3\right)\). Let \[\overrightarrow R(\theta,\phi)=\left\langle\cos\theta\sin\phi, \frac12\sin\theta\sin\phi,\frac13\cos\phi\right\rangle.\]
Then we have \begin{eqnarray*}
\frac{\partial}{\partial \theta}\overrightarrow R(\theta,\phi)&=&\left\langle-\sin\theta\sin\phi, \frac12\cos\theta\sin\phi,0\right\rangle\\
\frac{\partial}{\partial \phi}\overrightarrow R(\theta,\phi)&=&\left\langle\cos\theta\cos\phi, \frac12\sin\theta\cos\phi,-\frac13\sin\phi\right\rangle\\
\frac{\partial}{\partial \theta}\overrightarrow R(\theta,\phi)\times \frac{\partial}{\partial \phi}\overrightarrow R(\theta,\phi)&=& \mbox{det }\left|
\begin{array}{ccc}
\overrightarrow i & \overrightarrow j & \overrightarrow k\\
-\sin\theta\sin\phi & \frac12\cos\theta\sin\phi & 0 \\
\cos\theta\cos\phi & \frac12\sin\theta\cos\phi & -\frac13\sin\phi
\end{array}
\right|\\
&=&
-\frac16\cos\theta\sin^2\phi\overrightarrow i - \frac13\sin\theta\sin^2\phi\overrightarrow j- \frac12\sin\phi\cos\phi \overrightarrow k\\
\overrightarrow N\left(\frac{\pi}4,\frac{\pi}4\right)&=&-\left\langle
\frac{\sqrt 2}{24},\frac{\sqrt 2}{12},\frac14
\right\rangle.
\end{eqnarray*}
Thus, the equation of the tangent plane is the following:
\[\frac{\sqrt 2}{24}\left(x-\frac12\right)+\frac{\sqrt 2}{12}\left(y-\frac14\right)+\frac14\left(z-\frac{\sqrt 2}3\right)=0.\]
Practice problems
Problem 1. Find the tangent plane at \((3,4,7)\) to the surface given by its parametric equations:
\begin{eqnarray*}
x&=&5\cos s\\
y&=&5\sin s\\
z&=& t\\
0\leq&s&\leq 2\pi\\
-\infty < &t& < +\infty.
\end{eqnarray*}
- (A) \(x+y+z=5\cos s+5\sin s+t\)
- (B) \(3(x-5\cos s)+4(y-5\sin s)+(z-t)=0\)
- (C) \(z=5x+5y\)
- (D) \(4(x-3)+3(y-4)=0\)
- (E)
\(3x+4y=25\)
Notice that for \(s_0=\arcsin \left(\frac 45\right)\) and \(t_0=7\) we have \((x_0,y_0,z_0)=(x,y,z)(s_0,t_0)=(3,4,7)\).
The normal vector to the surface is parallel to \(\overrightarrow R_s\times\overrightarrow R_t\) where \[\overrightarrow R(s,t)=
\langle 5\cos s, 5\sin s, t\rangle.\]
We can now calculate the vectors \(\overrightarrow R_s\), \(\overrightarrow R_t\) and \(\overrightarrow R_s\times\overrightarrow R_t\):
\begin{eqnarray*}
\overrightarrow R_s&=&\langle -5\sin s,5\cos s,0\rangle\\
\overrightarrow R_t&=&\langle 0,0,1\rangle\\
\overrightarrow R_s\times\overrightarrow R_t&=&\mbox{det }\left|
\begin{array}{ccc}\overrightarrow i& \overrightarrow j& \overrightarrow k\\
-5\sin s&5\cos s&0\\ 0& 0&1
\end{array}
\right|=\langle 5\cos s,5\sin s, 0\rangle.
\end{eqnarray*}
Therefore \(\overrightarrow R_s\times\overrightarrow R_t(s_0,t_0)=\langle 3,4,0\rangle\) and the equation of the tangent plane is:
\[3(x-3)+4(y-4)=0.\]
The correct answer is E.
Problem 2.
Consider the surface given by the equation \(z=7-x-y\). Find the tangent plane of this surface at the point \((x_0,y_0)=(1,-3)\).
- (A) \(z=7-x-y\)
- (B) \(3(x+1)+(y+3)+z=0\)
- (C) \(3(x-1)+(y-3)+z-2=0\)
- (D) \(z=x+2y+3\)
- (E)
\(x+y+z=1\)
The given surface is a plane. Hence its tangent plane is itself and the correct answer is A.
Problem 3.
Find the tangent plane to the sphere \(x^2+y^2+z^2=9\) at the point \(\left(1,2,-2\right)\).
First solution. The tangent plane of the sphere is normal to the radius vector. Since the radius vector is \(\langle 1,2,-2\rangle\), a normal vector to the tangent plane is \(\langle 1, 2, -2\rangle\) and the equation is \[(x-1)+2(y-2)-2(z+2)=0.\]
Second solution.
Consider the surface \(z=-\sqrt{9-x^2-y^2}\). This is the lower hemisphere of the sphere \(x^2+y^2+z^2=9\). The lower hemisphere contains the point \((1,2,-2)\).
The normal vector to the tangent plane at \((x,y)\) is given by \[\overrightarrow N=\langle -z_x,-z_y,1\rangle=\left\langle- \frac{x}{\sqrt{9-x^2-y^2}},
-\frac{y}{\sqrt{9-x^2-y^2}},1\right\rangle.\]
The normal vector at the point \((x_0,y_0)=(1,2)\) is given by \[\overrightarrow N_0=\left\langle -\frac12,-1,1
\right\rangle\] and the equation of the plane is
\[-\frac12(x-1)-(y-2)+(z+2)=0.\]
Notice that this is the same solution as we obtained in the first way.
Problem 4.
Find the tangent plane to the ellipsoid \(\frac{x^2}{196}+y^2+z^2=1\) at the point \(\left(4,\frac37,\frac67\right)\).
First solution.
Consider the surface \(z=\sqrt{1-\frac{x^2}{196}-y^2}\). This is the upper part of the ellipsoid which contains the point
\(\left(4,\frac37,\frac67\right)\).
The normal vector to the tangent plane at \((x,y)\) is parallel to \[\overrightarrow N=\langle -z_x,-z_y,1\rangle=\left\langle \frac{x}{196\sqrt{1-\frac{x^2}{196}-y^2}}, \frac{y}{\sqrt{1-\frac{x^2}{196}-y^2}}
,1\right\rangle.\]
The normal vector at the point \((x_0,y_0)=\left(4,\frac37\right)\) is given by \[\overrightarrow N_0=\left\langle \frac1{42},\frac12,1
\right\rangle\] and the equation of the plane is
\[\frac1{42}(x-4)+\frac12\left(y-\frac37\right)+\left(z-\frac67\right)=0.\]
Second solution (using gradients).
When a surface is given by its implicit equation \(F(x,y,z)=0\) for a differentiable function \(F\), the normal vector at the point \((x_0,y_0,z_0)\) is parallel to \(\nabla F(x_0,y_0,z_0)\). Hence the normal vector is parallel to \(\nabla F=\left\langle\frac{1}{98} x, 2y,2z\right\rangle\) hence:
\[\overrightarrow N\left(4,\frac37,\frac67\right)=\left\langle \frac2{49},\frac{6}7,\frac{12}7\right\rangle.\]
The equation of the plane is:
\[\frac2{49}\cdot\left(x-4\right)+\frac67\cdot \left(y-\frac37\right)+\frac{12}7\cdot \left(z-\frac67\right)=0.\]
Problem 5.
Assume that \(S\) is a surface and \(M\) a point on \(S\). Assume that \(\alpha\) is a plane tangent to \(S\) at the point \(M\) and assume that \(\overrightarrow a\) and \(\overrightarrow b\) are two vectors in the plane \(\alpha\). Consider the following mathematical propositions:
- (I) The vector \(\overrightarrow a\times \overrightarrow b\) is also a vector in the tangent plane \(\alpha\).
- (II) The vector \(\overrightarrow a+\overrightarrow b\) is also a vector in the tangent plane \(\alpha\).
- (III) The vector \(\overrightarrow a\times \overrightarrow b\) is a vector normal to the tangent plane \(\alpha\).
Which of the following is true?
- (A) The propositions (I) and (II) are true for every surface \(S\).
- (B) The propositions (I) and (III) are true for every surface \(S\).
- (C) The propositions (II) and (III) are true for every surface \(S\).
- (D) All three propositions (I), (II), and (III) are true for all surfaces \(S\).
- (E)
There is a surface \(S\) for which none of the above propositions is true.
The correct answer is C. The vector \(\overrightarrow a+\overrightarrow b\) belongs to the plane determined by \(\overrightarrow a\) and \(\overrightarrow b\), while the vector \(\overrightarrow a\times\overrightarrow b\) is orthogonal to that plane.
