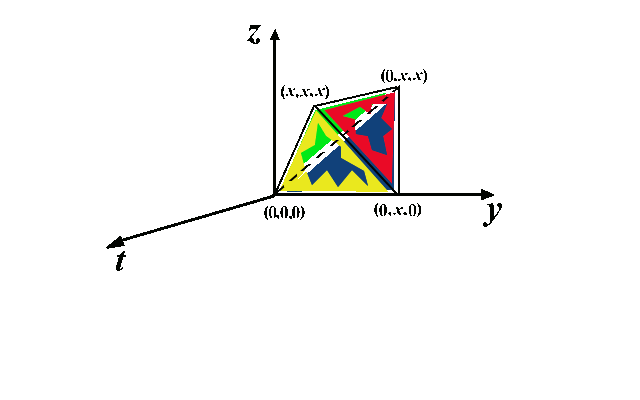Triple Integrals
Introduction
Motivated by the concept of double integrals, we want to consider the integrals of functions of three variables. The domain of integration will now be a three-dimensional solid region.
Triple integrals over rectangular boxes
Integral sums
Assume that \(f\) is a function defined on a rectangular box \([a,b]\times [c,d]\times [e,g]\) in the space \(\mathbb R^3\).
Consider three sequences of points \begin{eqnarray*}&&a=x_0\leq x_1\leq x_2\leq\cdots\leq x_n=b,\newline &&c=y_0\leq y_1\leq y_2\leq\cdots\leq y_m=d,\mbox{ and}\newline &&e=z_0\leq z_1\leq z_2\leq\cdots\leq z_p=g\end{eqnarray*} for \(m,n,p\in\mathbb N\). The box \([a,b]\times[c,d]\times[e,g]\) is the union of rectangles \([x_i,x_{i+1}]\times[y_j,y_{j+1}]\times[z_k,z_{k+1}]\) for each choice of \(i\), \(j\), and \(k\) such that \(i\in\{0,1,\dots, n-1\}\), \(j\in\{0,1,\dots, m-1\}\), and \(k\in\{0,1,\dots, p-1\}\). Denote these rectangles by \(R_1\), \(R_2\), \(\dots\), \(R_{mnp}\). Denote by \(A_i\) the area of the rectangle \(R_i\) and let \(c_i\) be an arbitrary point from the rectangle \(R_i\).
The integral sum (also known as the Riemann sum) corresponding to the partition into rectangles \(R_1\), \(\dots\), \(R_{mnp}\) with the points \(c_1\), \(\dots\), \(c_{mnp}\) is defined as \[S(f,R_1,\dots, R_{mnp}, c_1,\dots, c_{mnp})= f(c_1)\cdot A_1+ f(c_2)\cdot A_2+\cdots + f(c_{mnp})\cdot A_{mnp}.\]
The diameter of partition is defined as \[\delta(R_1, \dots, R_{mnp})=\max\{A_1,\dots ,A_{mnp}\}.\]
Definition of triple integrals over rectangular boxes
Consider the function \(f:[a,b]\times[c,d]\times[e,g]\to \mathbb R\), and consider the partitions of the box \([a,b]\times[c,d]\times[e,g]\) into smaller boxes. We say that the function \(f\) is integrable if the integral sums \(S(f,R_1, \dots, R_{mnp}, c_1, \dots, c_{mnp})\) converge as the diameters of partitions converge to \(0\).
Here is the formal definition:
Definition: Triple integral over rectangular box
The function \(f:[a,b]\times[c,d]\times[e,g]\to\mathbb R\) is integrable and its integral over the box \([a,b]\times[c,d]\times[e,g]\) is equal to \(I\in\mathbb R\) if for each \(\varepsilon > 0\) there exists \(\delta > 0\) such that for every partition \(\{R_1,\dots, R_{mnp}\}\) of \([a,b]\times[c,d]\times[e,f]\) with \(\delta(R_1,\dots, R_{mnp}) < \delta\) we have \[\left|S(f,R_1,\dots, R_{mnp},c_1,\dots, c_{mnp})-I\right| < \varepsilon\] for every choice of \(c_1\in R_1\), \(c_2\in R_2\), \(\dots\), \(c_{mnp}\in R_{mnp}\).
The value \(I\) from the previous definition is often denoted as \[I=\iiint_{[a,b]\times[c,d]\times[e,g]} f(x,y,z)\,dxdydz \quad\quad\quad \mbox{or} \quad\quad\quad I=\iiint_{[a,b]\times[c,d]\times[e,g]} f(x,y,z)\,dV.\]
Iterated integrals and Fubini’s theorem
Assume that \(f:[a,b]\times[c,d]\times[e,g]\to\mathbb R\) is an integrable function. For each fixed \((x,y)\in[a,b]\times[c,d]\) the function \(z\mapsto f(x,y,z)\) is a function of one variable and we can talk about single integral \(\int_e^g f(x,y,z)\,dz\). The result of integration will be a function in \((x,y)\) so we can talk about \(\int_a^b\int_c^d \left(\int_e^g f(x,y,z)\,dz\right)\,dydx\). This is called the iterated integral.
Fubini’s theorem in three dimension states that the iterated integrals are equal to the triple integral defined above.
Theorem (Fubini)
If \(f:[a,b]\times[c,d]\times[e,g]\to\mathbb R\) is a continuous function, then \begin{eqnarray*}\iiint_{[a,b]\times[c,d]\times[e,g]} f(x,y,z)\,dxdydz&=&\int_a^b \int_c^d\int_e^g f(x,y,z)\,dzdydx \newline &=&
\int_a^b\int_e^g \int_c^d f(x,y,z)\,dydzdx\newline &=&
\int_c^d\int_a^b \int_e^g f(x,y,z)\,dzdxdy\newline &=&
\int_c^d \int_e^g\int_a^b f(x,y,z)\,dxdzdy\newline &=&
\int_e^g\int_a^b \int_c^d f(x,y,z)\,dydxdz \newline &=&
\int_e^g\int_c^d\int_a^b f(x,y,z)\,dxdydz
.\end{eqnarray*}
Remark. Fubini’s theorem holds also if instead of continuity of \(f\) we assumed that \(f\) is bounded on \([a,b]\times[c,d]\times[e,g]\), the set of discontinuities consists of finitely many smooth surfaces, and the iterated integrals exist.
We will omit the proof of the theorem.
Triple integrals over general regions
Our goal now is to generalize the integration to include functions that are defined on regions that are not rectangular boxes.
Assume now that \(D\subseteq \mathbb R^3\) is a general region that is not necessarily a rectangular box. We can define the integral \(\iint_D f(x,y,z)\,dV\) in the following way. First, assume that \(R\) is a rectangle of the form \([a,b]\times[c,d]\times[e,g]\) for some \(a,b,c,d,e,g\in\mathbb R\). Then we define the function \(\hat f:R\to\mathbb R\) in the following way
\[\hat f(x,y,z)=\left\{\begin{array}{ll} f(x,y,z),& \mbox{ if } (x,y,z)\in D,\newline
0,&\mbox{ if } (x,y,z)\not\in D,\end{array}\right.\]
and we define \(\iiint_Df(x,y,z)\,dV\) as: \[\iint_Df(x,y,z)\,dV=\iiint_R\hat f(x,y,z)\,dV.\]
Practice problems
Problem 1. Evaluate the integral \[\iiint_S xyz\,dxdydz,\] where \(S\) is the rectangular box \(S=[0,2]\times[1,5]\times[-1,3]\).
The integral is equal to:
\begin{eqnarray*}
\int\int\int_S xyz\,dxdydz&=& \int_0^2\int_1^5\int_{-1}^3xyz\,dzdydx=
\int_0^2\int_1^5\left.\frac12 xyz^2\right|_{z=-1}^{z=3}\,dydx\newline
&=&\int_0^2\int_1^54xy\,dydx=\int_0^2\left.\frac42xy^2\right|_{y=1}^{y=5}\,dx\newline &=&48\int_0^2x\,dx=96.
\end{eqnarray*}
Problem 2. Evaluate the integral \[\iiint_S z\,dxdydz,\] where \(S\) is a triangular prism bounded by the planes \(x=0\), \(y=0\), \(z=0\), \(x=5\), and \(y+z=1\).
The bounds for integration are \(0\leq x\leq 5\), \(0\leq z\leq 1\), and \(0\leq y\leq 1-z\). Hence the integral becomes
\begin{eqnarray*}
\iiint_S z\,dxdydz&=& \int_0^5\int_0^1\int_0^{1-z}z\,dydzdx\\
&=&\int_0^5\int_0^1z(1-z)\,dzdx\\&=&\int_0^5\left(\frac12-\frac13\right)\,dx\\
&=&\frac5{6}.
\end{eqnarray*}
Problem 3. Find the volume of the solid in the first octant that is located between the surface \(y=z^2\) and the plane \(x+y=4\).
The volume is equal to the integral \(\iiint_S 1dV\), where \(S\) is the described solid.
The solid is shown in the picture below. You should imagine that the front green face is made of glass. Then the glass is broken and you can now see inside the blue wall (which belongs to the surface \(y=z^2\)), and the yellow wall on the back (which belongs to the plane \(x+y=4\)).
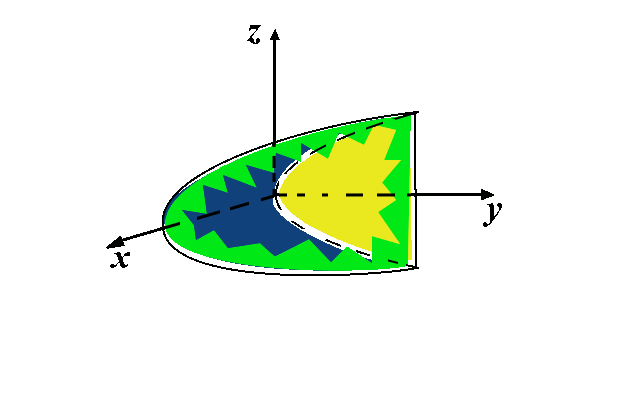
The solid \(S\) is given by:
\[S=\left\{(x,y,z): -2\leq z\leq 2, z^2\leq y\leq 4, 0\leq x\leq 4-y\right\}.\]
Hence the volume can be found in the following way:
\begin{eqnarray*}
\iiint_S 1\,dV&=&\int_{-2}^2\int_{z^2}^4\int_0^{4-y}1\,dxdydz=\int_{-2}^2\int_{z^2}^4 \left.x\right|_0^{4-y}\,dydz\newline &=&
\int_{-2}^2\int_{z^2}^4 (4-y)\,dydz=\int_{-2}^2\left. \left(4y-\frac{y^2}2\right)\right|_{z^2}^4\,dz
\newline &=&\int_{-2}^2\left(16-8-4z^2+\frac{z^4}{2}\right)\,dz= \left.\left(8z-\frac43z^3+\frac{z^5}{10}\right)\right|_{-2}^2\newline
&=&32-\frac{4}3\cdot 2^4+\frac{2^5}{5}=\frac{256}{15}.
\end{eqnarray*}
Problem 4. Evaluate the integral \[\int_{-1}^1\int_0^{z^2}\int_0^y \frac{z+\tan\frac{z}{x^2+y^2+1}}{x^2+y^2+1}\,dxdydz.\]
Let \(f(x,y,z)=\frac{z+\tan\frac{z}{x^2+y^2+1}}{x^2+y^2+1}\).
Since \(f(x,y,-z)=-f(x,y,z)\) and the domain of integration is symmetric with respect to \(xy\)-plane we get that the required integral is equal to \(0\).
Problem 5. For any bounded continuous function \(f\) the integral \(\int_0^x\int_0^y\int_0^zf(t)\,dtdzdy\) is equal to:
- (A)
\(0\)
- (B)
\(\int_0^xxf(t)\,dt\)
- (C)
\(\frac12\int_0^x(x-t)^2f(t)\,dt\)
- (D)
\(\int_0^x(y-x)f(y)dy\)
- (E)
\(xf(x)-\frac{x^2}2\)
We first draw the domain of integration. The variables are \(t\), \(y\), and \(z\) and we will draw the picture in the space were coordinate axes are \(t\), \(y\), and \(z\). The domain is the set of points \(S=\{(t,y,z): 0\leq y\leq x,
0\leq z\leq y,
0\leq t\leq z\}\).
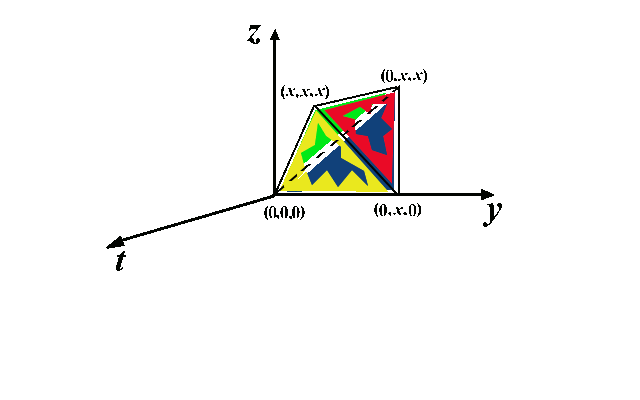
The equation of the plane that contains the blue triangle is \(t=0\), the equation of the plane of the red triangle is \(y=x\), the equation of the plane that contains the green triangle is \(z=y\), and the equation of the plane that contains the yellow triangle is \(z=t\).
Notice that the set \(S\) can be represented in the following way: \[S=\{(t,y,z):0\leq t\leq x, t\leq z\leq x, z\leq y\leq x\}.\] Therefore:
\begin{eqnarray*}
\int_0^x\int_0^y\int_0^zf(t)\,dtdzdy&=&\int_0^x\int_t^x\int_z^x f(t) \,dydzdt\\&=&
\int_0^xf(t)\cdot\int_t^x\int_z^x 1\,dydzdt\\
&=&\int_0^xf(t)\cdot\int_t^x(x-z)\,dzdt\\&=&\int_0^xf(t)\cdot \left.\left(xz-\frac{z^2}2\right)\right|_t^x\,dt\\
&=&\int_0^xf(t)\cdot \frac{2x(x-t)-(x^2-t^2)}2\,dt\\&=&\frac12\int_0^x(x-t)^2f(t)\,dt.
\end{eqnarray*}
Remark. The problem could be solved using the integration by parts from the single variable calculus.
We denote \(F(x)=\int_0^xf(t)\,dt\), \(G(x)=\int_0^xF(t)\,dt\), and \(H(x)=\int_0^xG(t)\,dt\). Then \(\int_0^x\int_0^y\int_0^zf(t)\,dtdzdy=
H(x)\). In order to prove that \(\int_0^x\frac{(x-t)^2}2f(t)\,dt=H(x)\) we use integration by parts:
\begin{eqnarray*}
\int_0^x\frac{(x-t)^2}2\,dF(t)&=&\left.F(t)\cdot \frac{(x-t)^2}2
\right]_0^x-\int_0^xF(t)(t-x)\,dt\\&=&
\int_0^x(x-t)\,dG(t)=\left.G(t)\cdot (x-t)\right]_0^x-\int_0^x G(t)\cdot (-1)\,dt\\&=& H(x).
\end{eqnarray*}
The correct answer is C.