Vector Fields. Parametric Equations of Curves and Surfaces
Vector fields
A function whose codomain is \(\mathbb R^2\) or \(\mathbb R^3\) is called a vector field. This name emphasize that the output of the function is a vector. Most vector functions that we will consider will have a domain that is a subset of \(\mathbb R\), \(\mathbb R^2\), or \(\mathbb R^3\).
An example of a vector field is the function \(\overrightarrow{F}:[0,5]\to\mathbb R\) defined as \[\overrightarrow F(t)=\langle 7t+5, t^2+4\rangle.\]
Parametric equations of curves
We will now see how vector fields whose domains are subsets of \(\mathbb R\) correspond to curves. Consider a vector field \(\overrightarrow{r}:[0,2\pi)\to\mathbb R^2\) defined as: \(\overrightarrow{r}(t)=\langle 3\cos t,3\sin t\rangle\). Each number \(t\in[0,2\pi)\) is mapped to a vector \(\langle 3\cos t,3\sin t\rangle\). Let us place this vector so its starting point is at \((0,0)\), and let us put green paint at the tip of the vector. Then as \(t\) ranges from \(0\) to \(2\pi\) the tip of the vector will leave a green trace. Since \((3\sin t)^2+(3\cos t)^2=1\), the tip of the vector will trace a green circle in the plane. The equation \(\overrightarrow r(t)=\langle 3\cos t, 3 \sin t\rangle\), \(t\in[0,2\pi)\) is called the parametric equations of the circle. We use plural here, because parametric equations are often written in the following way: \begin{eqnarray*} x(t)&=&3\cos t\newline y(t)&=&3\sin t\newline 0\leq&t&< 2\pi. \end{eqnarray*}
This way we can assign a curve to every vector field \(\overrightarrow r:[a,b]\to\mathbb R^2\) or \(\overrightarrow r:[a,b]\to\mathbb R^2\). The curve is obtained as a trace of the tip of the vector whose starting point is at the origin.
The formal definition is: A curve corresponding to the vector field \(\overrightarrow{r}:[a,b]\to\mathbb R^3\) is the image of the mapping \(t\mapsto (0,0,0)+\overrightarrow{r}(t)\).
Parametric equations of surfaces
In an analogy to the previous section, we can assign a surface to every vector field of the form \(\overrightarrow r: D\to\mathbb R^3\), where \(D\subseteq \mathbb R^2\) is a two-dimensional region.
Consider, for example, the following vector field: \(\overrightarrow r:[0,2\pi)\times[0,\pi]\to \mathbb R^2\) defined by \[\overrightarrow r(\theta,\phi)=\langle 3\cos\theta\sin\phi,3 \sin\theta\sin \phi,3\cos \phi\rangle.\] When \(\theta\) and \(\phi\) take all possible values in \([0,2\pi)\times[0,\pi]\) the tip of the vector \(\overrightarrow r\) will trace the sphere of radius \(3\). It is common to write these parametric equations in the form: \begin{eqnarray*} x(\theta,\phi)&=&3\cos\theta\sin\phi\\ y(\theta,\phi)&=&3\sin\theta\sin\phi\\ z(\theta,\phi)&=&3\cos\phi\\ 0\leq&\theta&< 2\pi\\ 0\leq&\phi&\leq\pi. \end{eqnarray*}
The number \(\phi\) is the angle between the vector \(\overrightarrow{r}(\theta, \phi)\) and the \(z\)-axis, while the number \(\theta\) is the angle between the \(x\)-axis and the projection of \(\overrightarrow r(\theta, \phi)\) to the \(xy\)-plane.
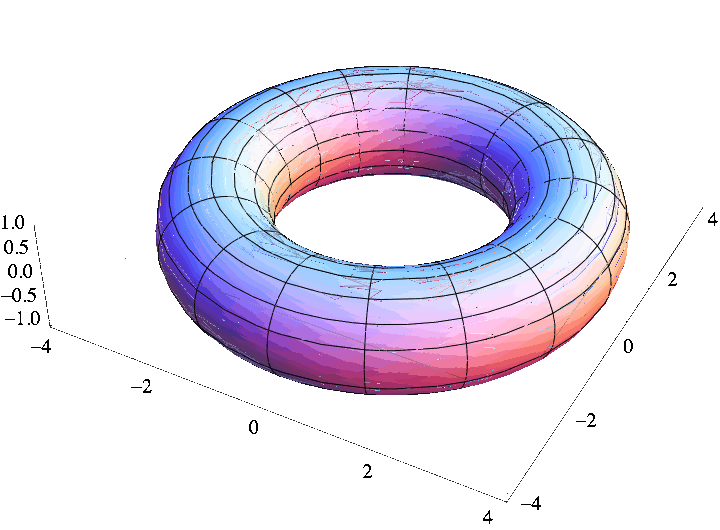
If we change the domain of the previous vector field to \([0,2\pi)\times \left[\frac{\pi}3,\frac{2\pi}3\right]\) then we obtain the sphere with two pieces removed (one near the north pole and one near the south pole). The picture below is obtained using the program Mathematica (wolfram.com) with the command:
ParametricPlot3D[{3 Cos[t] Sin[s], 3 Sin[t] Sin[s], 3 Cos[s]}, {t, 0, 2 Pi}, {s, Pi/3, 2 Pi/3}]

You may visit wolframalpha.com and type the previous command to obtain the same figure. By changing the range for \(t\) and \(s\) you can get different pieces of the sphere.
Let \(L_1\) be the line obtained as the intersection of the planes \(3x-y-z=3\) and \(x+y-z=1\). Let \(L_2\) be the line given by \(\langle -1,0,1\rangle+t\langle 2,1,1\rangle\).
- (a) Find the parametric equations of the line \(L_1\).
- (b) Prove that the lines \(L_1\) and \(L_2\) are skew lines.
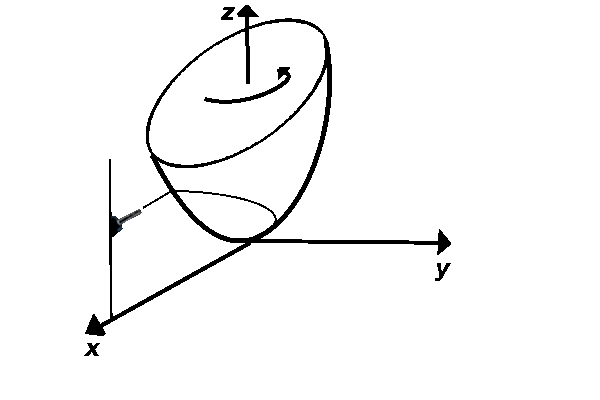
Initially, a paint nozzle is placed at the point \((100,0,0)\) and the nozzle is moving along the line parallel to the \(z\)-axis. The position of the nozzle at time \(t\) is \((100,0,t^2)\).
The paraboloid \(z=x^2+y^2\) is rotating around \(z\)-axis with constant angular speed. As time goes from \(0\) to \(1\), the paraboloid completes one rotation around the \(z\)-axis and ends up in the original position.
If the nozzle is spraying the paint towards the paraboloid the entire time, set up the integral (but do not evaluate) for the length of the curve that is painted on the surface during the time interval from \(t=0\) to \(t=1\). There is no gravity nor air resistance that could interfere with the painting.
Practice problems
- (A) \(\displaystyle x=2r\cos \theta\), \(\displaystyle y=r\sin \theta\), \(\displaystyle z=9-r^2\), \(\displaystyle 0\leq r\leq 3\), \(\displaystyle 0\leq \theta < 2\pi\)
- (B) \(\displaystyle x=2r\cos \theta\), \(\displaystyle y=2r\sin \theta\), \(\displaystyle z=5\sin r\), \(\displaystyle 0\leq r\leq 6\pi\), \(\displaystyle 0\leq \theta < 2\pi\)
- (C) \(\displaystyle x=2r\cos \theta\), \(\displaystyle y=2r\sin \theta\), \(\displaystyle z=5(2+\cos r)\), \(\displaystyle 0\leq r\leq 6\pi\), \(\displaystyle 0\leq \theta < 2\pi\)
- (D) \(\displaystyle x=r\cos \theta\), \(\displaystyle y=r\sin \theta\), \(\displaystyle z=\sqrt{9-r^2}\), \(\displaystyle 0\leq r\leq 3\), \(\displaystyle 0\leq \theta < 2\pi\)
- (E) \(\displaystyle x=r\cos \theta\), \(\displaystyle y=r\sin \theta\), \(\displaystyle z=9-r\), \(\displaystyle 0\leq r\leq 3\), \(\displaystyle 0\leq \theta < 2\pi\)
- (A) \(\displaystyle x=2r\cos \theta\), \(\displaystyle y=r\sin \theta\), \(\displaystyle z=9-r^2\), \(\displaystyle 0\leq r\leq 3\), \(\displaystyle 0\leq \theta < 2\pi\)
- (B) \(\displaystyle x=2r\cos \theta\), \(\displaystyle y=2r\sin \theta\), \(\displaystyle z=5\sin r\), \(\displaystyle 0\leq r\leq 6\pi\), \(\displaystyle 0\leq \theta < 2\pi\)
- (C) \(\displaystyle x=2r\cos \theta\), \(\displaystyle y=2r\sin \theta\), \(\displaystyle z=5(2+\cos r)\), \(\displaystyle 0\leq r\leq 6\pi\), \(\displaystyle 0\leq \theta < 2\pi\)
- (D) \(\displaystyle x=r\cos \theta\), \(\displaystyle y=r\sin \theta\), \(\displaystyle z=\sqrt{9-r^2}\), \(\displaystyle 0\leq r\leq 3\), \(\displaystyle 0\leq \theta < 2\pi\)
- (E) \(\displaystyle x=r\cos \theta\), \(\displaystyle y=r\sin \theta\), \(\displaystyle z=9-r\), \(\displaystyle 0\leq r\leq 3\), \(\displaystyle 0\leq \theta < 2\pi\)
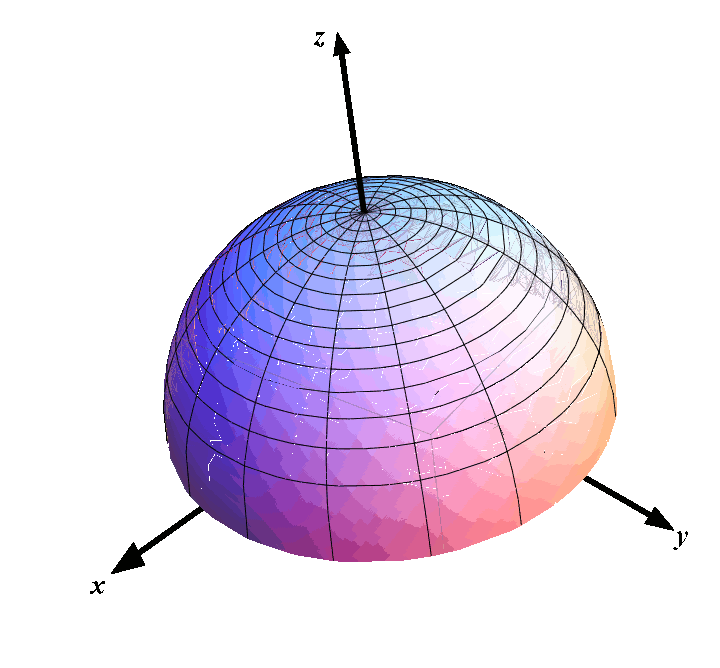
- (A) \(\displaystyle x=2r\cos \theta\), \(\displaystyle y=r\sin \theta\), \(\displaystyle z=9-r^2\), \(\displaystyle 0\leq r\leq 3\), \(\displaystyle 0\leq \theta < 2\pi\)
- (B) \(\displaystyle x=2r\cos \theta\), \(\displaystyle y=2r\sin \theta\), \(\displaystyle z=5\sin r\), \(\displaystyle 0\leq r\leq 6\pi\), \(\displaystyle 0\leq \theta < 2\pi\)
- (C) \(\displaystyle x=2r\cos \theta\), \(\displaystyle y=2r\sin \theta\), \(\displaystyle z=5(2+\cos r)\), \(\displaystyle 0\leq r\leq 6\pi\), \(\displaystyle 0\leq \theta < 2\pi\)
- (D) \(\displaystyle x=r\cos \theta\), \(\displaystyle y=r\sin \theta\), \(\displaystyle z=\sqrt{9-r^2}\), \(\displaystyle 0\leq r\leq 3\), \(\displaystyle 0\leq \theta < 2\pi\)
- (E) \(\displaystyle x=r\cos \theta\), \(\displaystyle y=r\sin \theta\), \(\displaystyle z=9-r\), \(\displaystyle 0\leq r\leq 3\), \(\displaystyle 0\leq \theta < 2\pi\)

- (A) \(\displaystyle x=2r\cos \theta\), \(\displaystyle y=r\sin \theta\), \(\displaystyle z=9-r^2\), \(\displaystyle 0\leq r\leq 3\), \(\displaystyle 0\leq \theta < 2\pi\)
- (B) \(\displaystyle x=2r\cos \theta\), \(\displaystyle y=2r\sin \theta\), \(\displaystyle z=5\sin r\), \(\displaystyle 0\leq r\leq 6\pi\), \(\displaystyle 0\leq \theta < 2\pi\)
- (C) \(\displaystyle x=2r\cos \theta\), \(\displaystyle y=2r\sin \theta\), \(\displaystyle z=5(2+\cos r)\), \(\displaystyle 0\leq r\leq 6\pi\), \(\displaystyle 0\leq \theta < 2\pi\)
- (D) \(\displaystyle x=r\cos \theta\), \(\displaystyle y=r\sin \theta\), \(\displaystyle z=\sqrt{9-r^2}\), \(\displaystyle 0\leq r\leq 3\), \(\displaystyle 0\leq \theta < 2\pi\)
- (E) \(\displaystyle x=r\cos \theta\), \(\displaystyle y=r\sin \theta\), \(\displaystyle z=9-r\), \(\displaystyle 0\leq r\leq 3\), \(\displaystyle 0\leq \theta < 2\pi\)
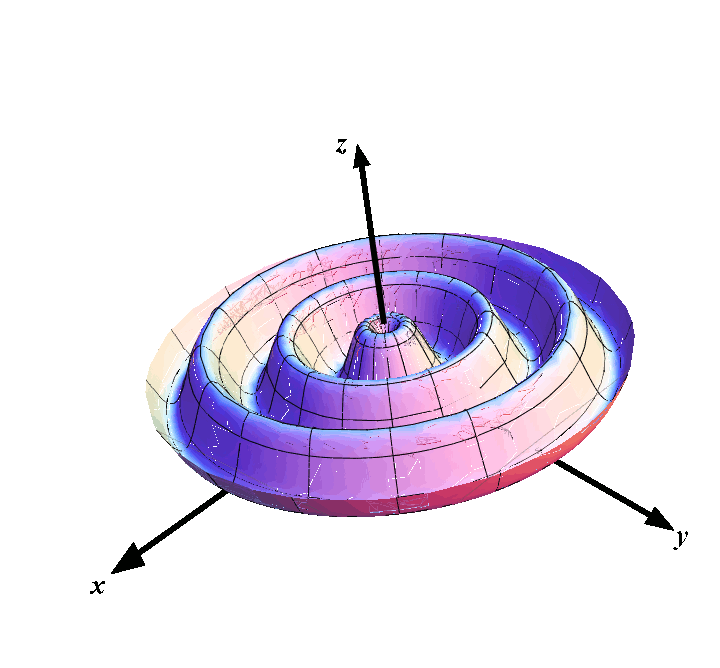
- (A) \(\displaystyle x=2r\cos \theta\), \(\displaystyle y=r\sin \theta\), \(\displaystyle z=9-r^2\), \(\displaystyle 0\leq r\leq 3\), \(\displaystyle 0\leq \theta < 2\pi\)
- (B) \(\displaystyle x=2r\cos \theta\), \(\displaystyle y=2r\sin \theta\), \(\displaystyle z=5\sin r\), \(\displaystyle 0\leq r\leq 6\pi\), \(\displaystyle 0\leq \theta < 2\pi\)
- (C) \(\displaystyle x=2r\cos \theta\), \(\displaystyle y=2r\sin \theta\), \(\displaystyle z=5(2+\cos r)\), \(\displaystyle 0\leq r\leq 6\pi\), \(\displaystyle 0\leq \theta < 2\pi\)
- (D) \(\displaystyle x=r\cos \theta\), \(\displaystyle y=r\sin \theta\), \(\displaystyle z=\sqrt{9-r^2}\), \(\displaystyle 0\leq r\leq 3\), \(\displaystyle 0\leq \theta < 2\pi\)
- (E) \(\displaystyle x=r\cos \theta\), \(\displaystyle y=r\sin \theta\), \(\displaystyle z=9-r\), \(\displaystyle 0\leq r\leq 3\), \(\displaystyle 0\leq \theta < 2\pi\)
- (A) \(x=t\), \(y=t^2+r^2+(t^2+r^2)^2\), \(z=r\)
- (B) \(x=t\), \(y=(t^2+r^2)^2\), \(z=r\)
- (C) \(x=t\), \(y=\sqrt{t^2+r^2}^3\), \(z=r\)
- (D) \(x=t\), \(y=(t^2+r^2)^3\), \(z=r\)
- (E) \(x=t\), \(y=\sqrt{t^2+r^2}^3+(t^2+r^2)^3\), \(z=r\)
- (A) \(x=t\), \(y=t^2+r^2+(t^2+r^2)^2\), \(z=r\)
- (B) \(x=t\), \(y=(t^2+r^2)^2\), \(z=r\)
- (C) \(x=t\), \(y=\sqrt{t^2+r^2}^3\), \(z=r\)
- (D) \(x=t\), \(y=(t^2+r^2)^3\), \(z=r\)
- (E) \(x=t\), \(y=\sqrt{t^2+r^2}^3+(t^2+r^2)^3\), \(z=r\)
- (A) \(x=4\cos\theta\sin\phi\), \(y=-5+2\sin\theta\sin\phi\), \(z=5\cos\phi\), \(0\leq \theta < 2\pi\), \(0\leq \phi\leq \pi\).
- (B) \(x=16\cos\theta\sin\phi\), \(y=-5+4\sin\theta\sin\phi\), \(z=25\cos\phi\), \(0\leq \theta\leq \pi\), \(0\leq \phi < 2\pi\).
- (C) \(x=5\cos\theta\sin\phi\), \(y=-5+2\sin\theta\sin\phi\), \(z=3\cos\phi\), \(0\leq \theta < 2\pi\), \(0\leq \phi\leq \pi\).
- (D) \(x=16\cos\theta\sin\phi\), \(y=-5+4\sin\theta\sin\phi\), \(z=25\cos\phi\), \(0\leq \theta\leq \pi\), \(0\leq \phi\leq \pi\).
- (E) \(x=\cos\theta\sin\phi\), \(y=-3+\sin\theta\sin\phi\), \(z=\cos\phi\), \(0\leq \theta < 2\pi\), \(0\leq \phi\leq \pi\).