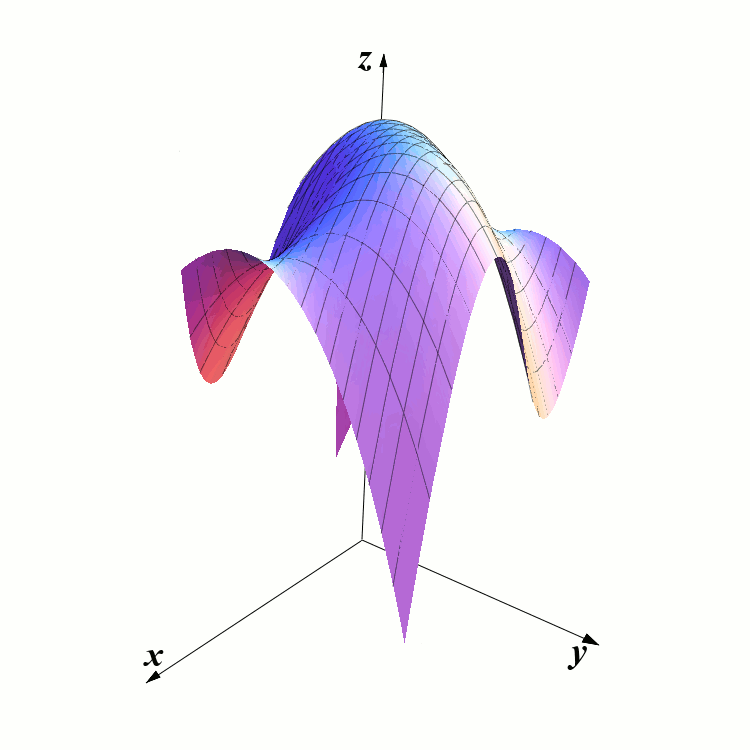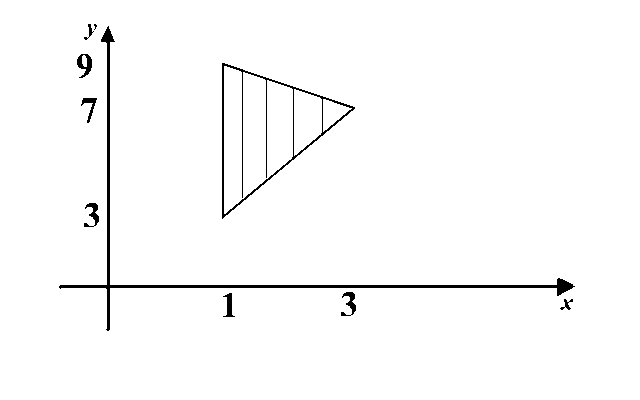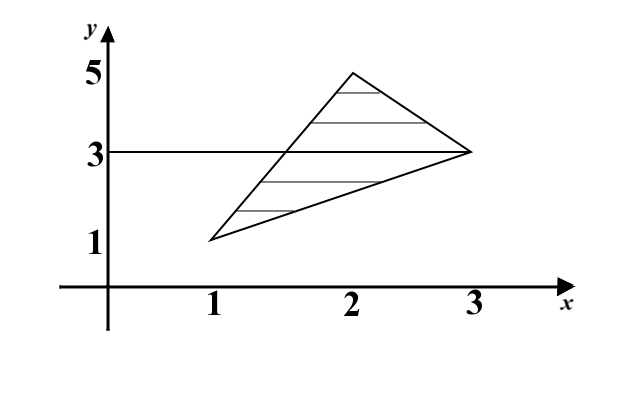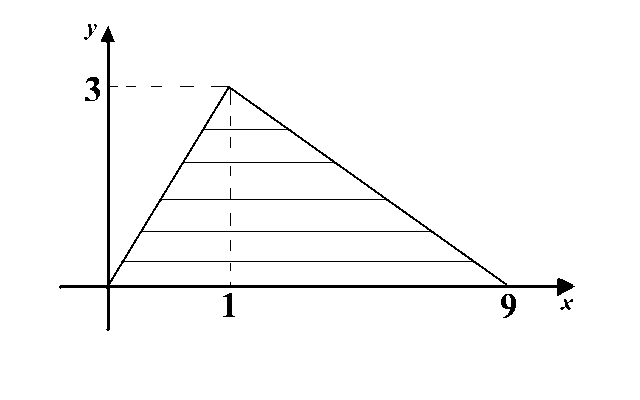Double Integrals
Motivation
In the single-variable calculus, one way to understand definite integrals was to treat them as the areas below the graphs of the curves. We can generalize this concept to the case of functions that depend on two variables. The graphs are now surfaces in three dimensional space, and the double integral is the volume below the graph and above the domain. (As before, the volumes of the portions of the solids below the \(xy\)-plane are taken with negative sign).
Double integrals over rectangles
Integral sums
The definite integral in the single-variable calculus was defined as the limit of integral sums. We take an analogous approach in multivariable calculus.
Assume that \(f\) is a function defined on a rectangle \([a,b]\times [c,d]\) in the plane \(\mathbb R^2\).
Consider two sequences of points \(a=x_0\leq x_1\leq x_2\leq\cdots\leq x_n=b\) and \(c=y_0\leq y_1\leq\cdots\leq y_m=d\) for \(m,n\in\mathbb N\). The rectangle \([a,b]\times[c,d]\) is the union of rectangles \([x_i,x_{i+1}]\times[y_j,y_{j+1}]\) for each choice of \(i\) and \(j\) such that \(i\in\{0,1,\dots, n-1\}\) and \(j\in\{0,1,\dots, m-1\}\). Denote these rectangles by \(R_1\), \(R_2\), \(\dots\), \(R_{mn}\). Denote by \(A_i\) the area of the rectangle \(R_i\) and let \(c_i\) be an arbitrary point from the rectangle \(R_i\).
The integral sum (also known as the Riemann sum) corresponding to the partition into rectangles \(R_1\), \(\dots\), \(R_{mn}\) with the points \(c_1\), \(\dots\), \(c_{mn}\) is defined as \[S(f,R_1,\dots, R_{mn}, c_1,\dots, c_{mn})= f(c_1)\cdot A_1+ f(c_2)\cdot A_2+\cdots + f(c_{mn})\cdot A_{mn}.\]
The diameter of partition is defined as \[\delta(R_1, \dots, R_{mn})=\max\{A_1,\dots ,A_{mn}\}.\]
Example
The following two pictures illustrate the previous concept. The first one shows the graph of a function \(f\). The second picture shows the partition of the domain into six rectangles and a parallelepiped on top of each of the rectangles. The height of the first parallelepiped is \(f(c_1)\), where \(c_1\) is a point inside \(R_1\). The points \(c_2\), \(\dots\), \(c_6\) are not marked in the picture - so you have to imagine them. Then \(S\) is equal to the total volume of the six parallelepipeds.
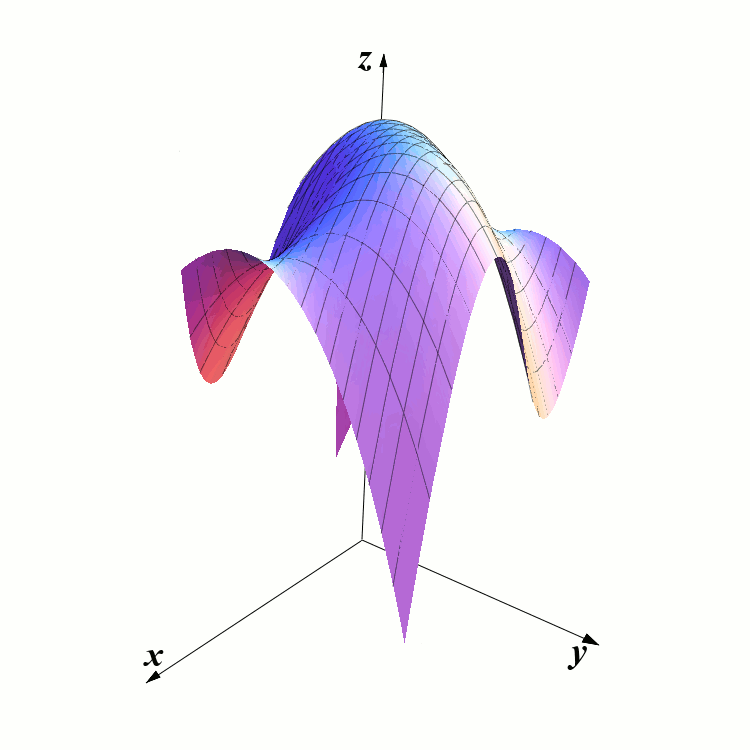
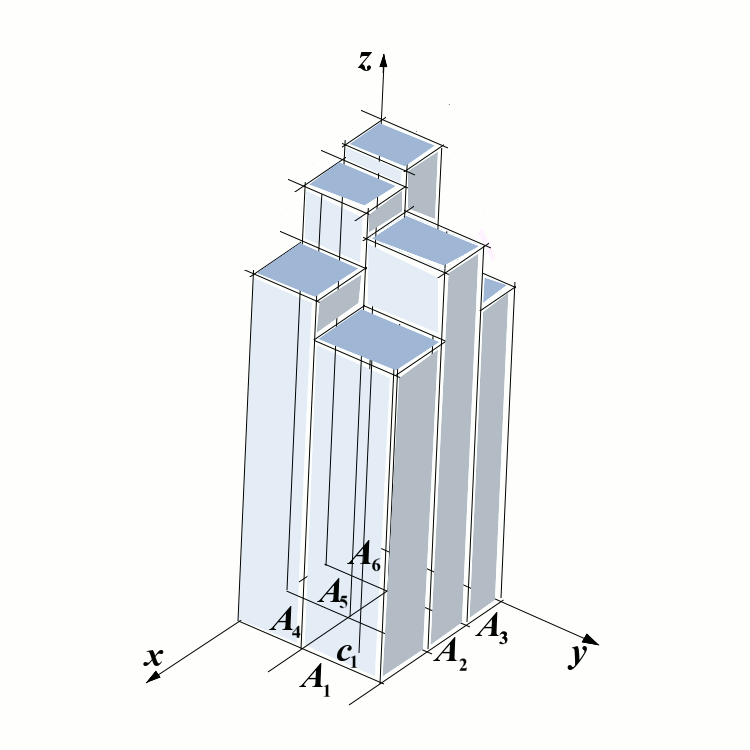
The definition of double integral over the rectangle
Consider the function \(f:[a,b]\times[c,d]\to \mathbb R\), and consider the partitions of the rectangle \([a,b]\times[c,d]\) into smaller rectangles. We say that the function \(f\) is integrable if the integral sums \(S(f,R_1, \dots, R_{mn}, c_1, \dots, c_{mn})\) converge as the diameters of partitions converge to \(0\).
Here is the formal definition:
Definition: Double integral over the rectangle
The function \(f:[a,b]\times[c,d]\to\mathbb R\) is integrable and its integral over the rectangle \([a,b]\times[c,d]\) is equal to \(I\in\mathbb R\) if for each \(\varepsilon > 0\) there exists \(\delta > 0\) such that for every partition \(\{R_1,\dots, R_{mn}\}\) of \([a,b]\times[c,d]\) with \(\delta(R_1,\dots, R_{mn}) < \delta\) we have \[\left|S(f,R_1,\dots, R_{mn},c_1,\dots, c_{mn})-I\right| < \varepsilon\] for every choice of \(c_1\in R_1\), \(c_2\in R_2\), \(\dots\), \(c_{mn}\in R_{mn}\).
The value \(I\) from the previous definition is often denoted as \[I=\iint_{[a,b]\times[c,d]} f(x,y)\,dxdy \quad\quad\quad \mbox{or} \quad\quad\quad I=\iint_{[a,b]\times[c,d]} f(x,y)\,dA.\]
Approximate evaluation of double integrals
Before developing the methods for evaluating double integrals let us first consider the following example in which we evaluate the integral sum.
Example 1
Let \(f:[1,5]\times[2,7]\to\mathbb R\) be the function defined as \(f(x,y)=37-x-2y\). Consider the partition of \([1,5]\times [2,7]\) determined by the points \(x_0=1\), \(x_1=3\), \(x_2=4\), \(x_3=5\), \(y_0=2\), \(y_1=5\), \(y_2=7\). Assume that in each rectangle \(R_i\) (for each \(i\in\{1,2,\dots, 6\}\)) the point \(c_i\) is chosen to be its intersection of diagonals. Evaluate \(S(f,R_1, \dots, R_6, c_1, \dots, c_6)\).
Let us denote \(R_1=[1,3]\times[2,5]\), \(R_2=[3,4]\times[2,5]\), \(R_3=[4,5]\times[2,5]\), \(R_4=[1,3]\times[5,7]\), \(R_5=[3,4]\times[5,7]\), and \(R_6=[4,5]\times[5,7]\). Then we have \(c_1=\left(2,\frac{7}2\right)\), \(c_2=\left(\frac72,\frac{7}2\right)\), \(c_3=\left(\frac92,\frac{7}2\right)\),
\(c_4=\left(2,6\right)\), \(c_5=\left(\frac72,6\right)\), and \(c_6=\left(\frac92,6\right)\).
We now have: \begin{eqnarray*} S(f,R_1,\dots, R_6,c_1,\dots, c_6)&=& f\left(2,\frac72\right)\cdot 6+f\left(\frac72,\frac72\right)\cdot 3+ f\left(\frac92,\frac72\right)\cdot 3\newline &&+ f\left(2,6\right)\cdot 4+f\left(\frac72,6\right)\cdot 2+f\left(\frac92,6\right)\cdot 2 \newline &=& 28\cdot 6+26.5\cdot 3+ 25.5\cdot 3+ 23\cdot 4+21.5\cdot 2+20.5\cdot 2\newline &=&500.\end{eqnarray*}
Iterated integrals
Assume that \(f:[a,b]\times[c,d]\to\mathbb R\) is an integrable function. For each fixed \(x\in[a,b]\) the function \(y\mapsto f(x,y)\) is a function of one variable and we can talk about single integral \(\int_c^d f(x,y)\,dy\). The result of integration will be a function in \(x\) so we can talk about \(\int_a^b \left(\int_c^d f(x,y)\,dy\right)\,dx\). This is called the iterated integral.
Example 2
Let \(f:[-1,3]\times[2,5]\to\mathbb R\) be a function defined as \(f(x,y)=10-3x^2-2y\). Find the iterated integrals \[\int_{-1}^3\left(\int_2^5 f(x,y)\,dy\right)\,dx \quad\quad\quad \mbox{and}\quad\quad\quad \int_2^5\left(\int_{-1}^3f(x,y)\,dx\right)\,dy.\]
- Evaluation of \(I_1=\int_{-1}^3\left(\int_2^5 f(x,y)\,dy\right)\,dx \).
First we find the integral \(\int_2^5 f(x,y)\,dy\):
\begin{eqnarray*}
\int_2^5 f(x,y)\,dy&=& \int_2^5 \left(10-3x^2-2y\right)\,dy= \left. \left(10y-3x^2y-y^2\right)\right|_{2}^5=30-9x^2-21=9-9x^2.
\end{eqnarray*}
Therefore
\begin{eqnarray*}
I_1&=&\int_{-1}^3\left(\int_2^5 f(x,y)\,dy\right)\,dx=\int_{-1}^3\left(9-9x^2\right)\,dx=\left.\left(9x-3x^3\right)\right|_{-1}^3=36-3\cdot 28=-48.
\end{eqnarray*}
- Evaluation of \(I_2= \int_2^5\left(\int_{-1}^3f(x,y)\,dx\right)\,dy\).
As in the case of \(I_1\) we first find the inner integral:
\begin{eqnarray*}
\int_{-1}^3 f(x,y)\,dx&=&\int_{-1}^3\left(10-3x^2-2y\right)\,dx=\left.\left( 10x-x^3-2xy\right)\right|_{-1}^3=40-28-8y=12-8y.
\end{eqnarray*}
Thus:
\begin{eqnarray*}
I_2&=&\int_2^5\left(\int_{-1}^3f(x,y)\,dx\right)\,dy= \int_2^5\left(12-8y\right)\,dy=\left.\left(12y-4y^2\right)\right|_2^5=36-4\cdot(25-4)=-48.
\end{eqnarray*}
We notice that in the previous example the values of the iterated integrals are the same. This is true in general, and this fact is known as the Fubini’s theorem. Fubini’s theorem also states that the iterated integrals are equal to the double integral defined above.
Theorem (Fubini)
If \(f:[a,b]\times[c,d]\to\mathbb R\) is a continuous function, then \[\iint_{[a,b]\times[c,d]} f(x,y)\,dxdy=\int_a^b \int_c^d f(x,y)\,dydx=\int_c^d\int_a^bf(x,y)\,dxdy.\]
Remark. Fubini’s theorem holds also if instead of continuity of \(f\) we assumed that \(f\) is bounded on \([a,b]\times[c,d]\), the set of discontinuities consists of finitely many smooth curves, and the iterated integrals exist.
The proof of Fubini’s theorem will be omitted here.
Double integrals over general regions
So far we dealt only with functions that are defined over the rectangles and we were able to define their integrals. These integrals represent volumes of the solid regions below the graph of the function \(z=f(x,y)\) and above the rectangle on which the function is defined. The portions of the functions below the \(xy\)-plane are taken with the negative sign.
Assume now that \(D\subseteq \mathbb R^2\) is a general region that is not necessarily a rectangle. We can define the integral \(\iint_D f(x,y)\,dxdy\) in the following way. First, assume that \(R\) is a rectangle of the form \([a,b]\times[c,d]\) for some \(a,b,c,d\in\mathbb R\). Then we define the function \(\hat f:R\to\mathbb R\) in the following way
\[\hat f(x,y)=\left\{\begin{array}{ll} f(x,y),& \mbox{ if } (x,y)\in D,\newline
0,&\mbox{ if } (x,y)\not\in D,\end{array}\right.\]
and we define \(\iint_Df(x,y)\,dxdy\) as: \[\iint_Df(x,y)\,dxdy=\iint_R\hat f(x,y)\,dxdy.\]
Example 3 Find the integral \(\iint_D \left(3-x-y^2\right)\,dxdy\) where \(D\) is the region in plane defined as: \[D=\left\{ (x,y): 1\leq x\leq 9, 0\leq y\leq \sqrt x\right\}.\]
First solution.
It is a good idea to draw the picture of domain of integration whenever possible. Here we draw the domain \(D\) as follows:
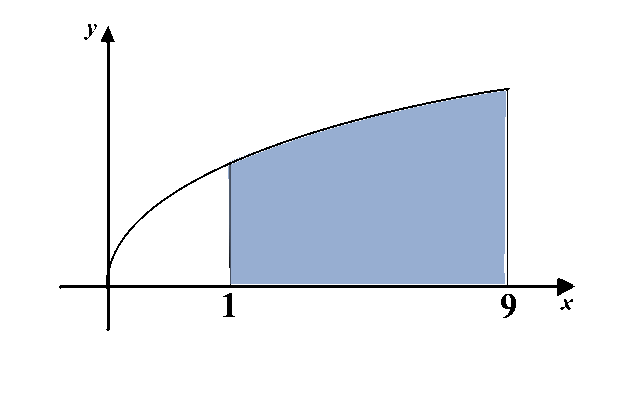
Let \(R=[1,9]\times[0,3]\). Then we have \(D\subseteq R\), and we can define \[\hat f(x,y)=\left\{\begin{array}{ll} f(x,y),& \mbox{ if } (x,y)\in D,\newline
0,&\mbox{ if } (x,y)\not\in D.\end{array}\right.\]
According to Fubini’s theorem we have
\[\iint_D f(x,y)\,dxdy=\int_0^9 \left(\int_0^3 \hat f(x,y)\,dy\right)\,dx.\]
Let us consider the inner integral, \(\int_0^3 \hat f(x,y)\,dy\). Let us study the range for \(y\) such that \(\hat f(x,y)\neq 0\). We keep \(x\) fixed, and \(y\) varies. The picture here is the fastest way to give us an idea for this range: the required range is \(0\leq y\leq \sqrt x\) (this is also evident from the definition of \(D\)). Therefore, \begin{eqnarray*}\int_0^3 \hat f(x,y)\,dy&=&\int_0^{\sqrt x}f(x,y)\,dy=\int_0^{\sqrt x}\left(3-x-y^2\right)\,dy\newline
&=&\left.\left(3y-xy-\frac13y^3\right)\right|_0^{\sqrt x}= 3\sqrt x-x\sqrt x-\frac13 x\sqrt x\newline
&=&3x-\frac43 x^{\frac32}.
\end{eqnarray*}
The integral now becomes:
\begin{eqnarray*}
\iint_Df(x,y)\,dxdy&=& \int_1^9\left(3\sqrt x-\frac43x^{\frac32}\right)\,dx=
\left.\left(3\cdot \frac23x^{\frac32}-\frac43\cdot \frac25\cdot x^{\frac52}\right)\right|_1^9
\newline &=& 2\cdot 26-\frac{8}{15}\cdot \left(3^5-1^5\right)=52-\frac{8\cdot 242}{15}\newline &=&-\frac{1156}{15}.
\end{eqnarray*}
Second solution.
We could also solve the problem in another way, as an iterated integral \(\int_0^3\int_1^9 \hat f(x,y)\,dxdy\). This time, the inner integral is \(\int_1^9 \hat f(x,y)\,dx\) and the integral of the function \(\hat f\) is evaluated with \(y\) being fixed. We want to find those values of \(y\) for which \(\hat f(x,y)\neq 0\) (and hence \(\hat f(x,y)=f(x,y)\)). The range for \(x\) depends on \(y\) in the following way: If \(0\leq y\leq 1\), then \(1\leq x\leq 9\), while if \(1\leq y\leq 3\), then \(y^2\leq x\leq 9\). Therefore for \(y\in [0,1]\),
\begin{eqnarray*}
\int_1^9\hat f(x,y)\,dx&=&\int_1^9\left(3-x-y^2\right)\,dx=\left.\left(
3x-\frac{x^2}2-y^2x\right)\right|_1^9=24-40-8y^2\newline
&=&-16-8y^2.
\end{eqnarray*}
For \(y\in[1,3]\) we have:
\begin{eqnarray*}\int_1^9\hat f(x,y)\,dx&=&\int_{y^2}^9 f(x,y)\,dx=
\int_{y^2}^9 \left(3-x-y^2\right)\,dx=\left.\left(3x-\frac{x^2}2-y^2x\right)\right|_{y^2}^9\newline
&=&27-\frac{81}2-9y^2-3y^2+\frac{y^4}2+y^4\newline &=&
-\frac{27}2-12y^2+\frac32y^4.
\end{eqnarray*}
The integral now becomes \begin{eqnarray*}
\iint_Df(x,y)\,dxdy&=&\int_0^1\left(-16-8y^2\right)\,dy+\int_1^3 \left(-\frac{27}2-12y^2+\frac32y^4\right)\,dy\newline &=&
\left.\left(-16y-\frac83y^3\right)\right|_0^1+
\left.\left(-\frac{27}2y-4y^3+\frac{3}{10}y^5
\right)\right|_1^3\newline
&=&-16-\frac83 -\frac{81}2-4\cdot 27+\frac{729}{10}+\frac{27}2+4-\frac3{10}\newline
&=&-\frac{1156}{15}.
\end{eqnarray*}
Practice problems
Problem 1. Find the integral \[\iint_{R}f(x,y)\,dxdy,\] where \(f(x,y)=11-2x-3y^2\) and \(R\) is the rectangle \([1,3]\times[-2,5]\).
Using Fubini’s theorem the given integral is equal to the iterated integral, and we obtain:
\begin{eqnarray*}
\int_R f(x,y)\,dxdy&=&\int_1^3\int_{-2}^5\left(11-2x-3y^2\right)\,dydx=
\int_1^3\left.\left(11y-2xy-y^3\right)\right|_{-2}^5\,dx\newline
&=&\int_1^3\left(11\cdot 7-2x\cdot 7-125-8\right)\,dx=\int_1^3\left(-14x-56\right)\,dx\newline &=& \left.\left(-7x^2-56x\right)\right|_1^3=-168.
\end{eqnarray*}
Problem 2. Let \(T\) be the region bounded by the triangle with vertices \((1,3)\), \((1,9)\), and \((3,7)\). Then the double integral \(\iint_T f(x,y)\,dA\) is equal to the following iterated integral:
- (A) \(\int_3^9\int_1^3 f(x,y)\,dydx\)
- (B)
\(\int_3^9\int_1^3 f(x,y)\,dxdy\)
- (C)
\(\int_1^3\int_{2y+1}^{-y+10}f(x,y)\,dxdy\)
- (D)
\(\int_1^3\int_{2x+1}^{-x+10}f(x,y)\,dydx\)
- (E)
\(\int_3^9\int_{\frac{y-1}2}^{-y+10}f(x,y)\,dxdy\)
We first draw the region \(T\) over which we are integrating the function \(f\).
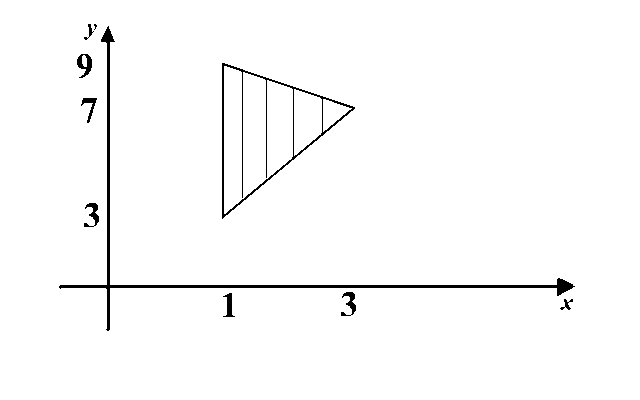
The equation of the line connecting points \((1,9)\) and \((3,7)\) is \(y=-x+10\), while the equation of the line connecting points \((1,3)\) and \((3,7)\) is \(y=2x+1\). Therefore the region of integration can be written as:
\[T=\left\{(x,y): 1\leq x\leq 3, 2x+1\leq y\leq -x+10\right\}.\] The integral is equal to: \[\iint_T f(x,y)\,dA= \int_1^3\int_{2x+1}^{-x+10}f(x,y)\,dydx.\]
The correct answer is D.
Problem 3. Let \(T\) be the region bounded by the triangle with vertices \((1,1)\), \((3,3)\), and \((2,5)\). Let \(f:T\to\mathbb R\) be a bounded and continuous function. Consider the following five quantities:
\begin{eqnarray*} I&=& \iint_T f(x,y)\,dA, \newline
I_1&=& \int_1^2\int_x^{\frac{x+3}4} f(x,y)\,dydx+\int_2^3 \int_x^{\frac{9-x}2}f(x,y)\,dydx ,\newline
I_2&=& \int_1^3\int_{\frac{y+3}4}^{y} f(x,y)\,dxdy+\int_3^5 \int_{\frac{y+3}4}^{\frac{9-y}2}f(x,y)\,dxdy, \newline
I_3&=& \int_1^2\int_{x}^{4x-3}f(x,y)\,dydx+\int_2^3\int_x^{-2x+9}f(x,y)\,dydx ,\newline
I_4&=&\int_1^3\int_{y}^{4y-3}f(x,y)\,dxdy+\int_3^5\int_y^{-2y+9}f(x,y)\,dxdy.
\end{eqnarray*}
The following equalities hold for every bounded and continuous function \(f\):
- (A) \(I=I_1=I_2\)
- (B)
\(I=I_2=I_3\)
- (C)
\(I=I_3=I_4\)
- (D)
\(I=I_4=I_1\)
- (E)
\(I=I_1=I_3\)
We first draw the region \(T\) over which we are integrating the function \(f\).
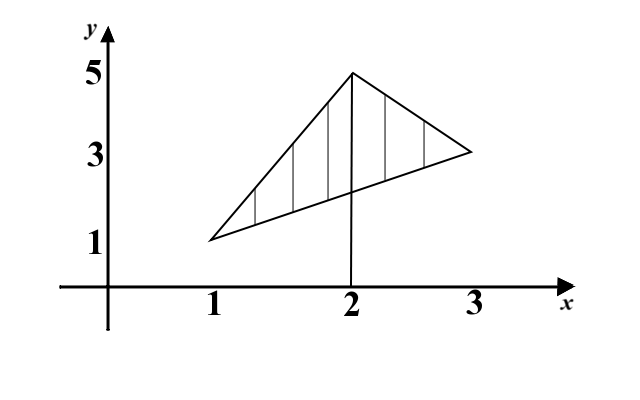
The equation of the line connecting points \((1,1)\) and \((3,3)\) is \(y=x\), the equation of the line connecting points \((1,1)\) and \((2,5)\) is \(y=4x-3\), and the equation of the line connecting the points \((2,5)\) and \((3,3)\) is \(y=-2x+9\). The region of integration can be written as:
\[T=\left\{(x,y): 1\leq x\leq 2, x\leq y\leq 4x-3\right\}\cup
\left\{(x,y): 2\leq x\leq 3, x\leq y\leq -2x+9\right\}.\] The integral is equal to: \[\iint_T f(x,y)\,dA= \int_1^2\int_{x}^{4x-3}f(x,y)\,dydx+\int_2^3\int_x^{-2x+9}f(x,y)\,dydx.\]
We could also write the region \(T\) as the following union:
\[T=\left\{(x,y):1\leq y\leq 3, \frac{y+3}4\leq x\leq y\right\} \cup \left\{(x,y): 3\leq y\leq 5, \frac{y+3}4\leq x\leq \frac{9-y}2\right\}.\]
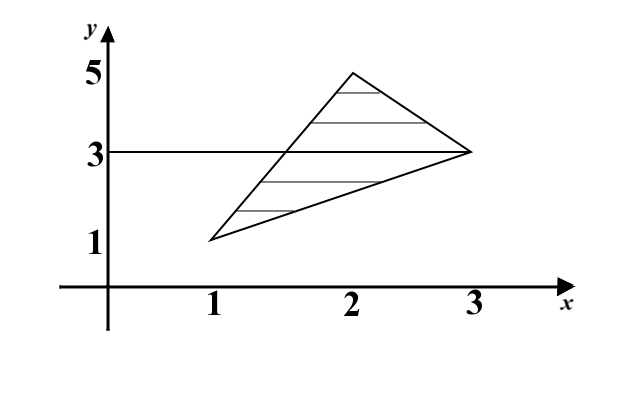
Now the integral is equal to:
\[\iint_Tf(x,y)\,dA=\int_1^3\int_{\frac{y+3}4}^{y} f(x,y)\,dxdy+\int_3^5 \int_{\frac{y+3}4}^{\frac{9-y}2}f(x,y)\,dxdy.\]
Thus, the correct answer is B.
Problem 4. Evaluate the integral \[\int_0^5\int_y^5\frac{\sin x}x\,dxdy.\]
Draw the picture of the region of integration!
The region of integration is a triangle with vertices \((0,0)\), \((5,0)\), and \((5,5)\). We can also describe this region \(D\) in the following way:
\[D=\{(x,y): 0\leq x\leq 5, 0\leq y\leq x\}.\]
Using Fubini’s theorem the integral becomes:
\begin{eqnarray*}\int_0^5\int_y^5\frac{\sin x}{x}\,dxdy&=&\int_0^5\int_0^x\frac{\sin x}x\,dydx=\int_0^5\left.\left(\frac{\sin x}xy\right)\right|_0^x\,dx \newline
&=& \int_0^5\sin x\,dx=\left.-\cos x\right|_0^5=1-\cos 5.
\end{eqnarray*}
Problem 5. Find the integral \[\int_{R}f(x,y)\,dxdy,\] where \(f(x,y)=50-8xy\) and \(R\) is the triangle with vertices \((0,0)\), \((9,0)\), and \((1,3)\).
We first draw the region \(R\) over which we are integrating the function \(f\).
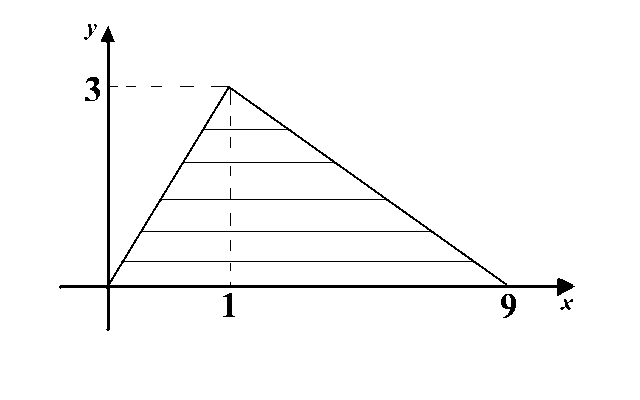
The region of integration is: \[R=\left\{(x,y): 0\leq y\leq 3, \frac y3\leq x\leq 9-\frac{8y}3\right\}.\]
We can now proceed to evaluate the integral
\begin{eqnarray*}
\int_R f(x,y)\,dxdy&=&\int_0^3\int_{\frac y3}^{9-\frac{8y}3}\left(50-8xy\right)\,dxdy= \int_0^3\left.\left(50x-4x^2y\right)\right|_{\frac y3}^{9-\frac{8y}3}\,dy
\newline
&=&\int_0^3\left( 50\cdot (9-3y)-4y\cdot \left(81-48y+7y^2\right)\right)\,dy \newline
&=&\int_0^3\left(450-474y+48\cdot 4y^2-28y^3\right)\,dy\newline &=&
\left.\left(450y-237y^2+64 y^3-7y^4\right)\right|_0^3\newline
&=&378
\end{eqnarray*}