Lagrange Multipliers
Conditional extremal value problems
Our goal is to solve the problems like this one:
Example 1.
Find the points \((x,y)\) on the curve \(x^2+y^2=1\) for which the quantity \(f(x,y)=xy\) is maximal.
This problem can be solved using techniques from elementary mathematics, but we’ll resist that temptation. In fact, we’ll use an even simpler example to illustrate the technique of Lagrange multipliers.
Example 2
Find the maximum of the function \(f(x,y)=\frac{x^2}9+y^2\) if the real numbers \(x\) and \(y\) satisfy \(x^2+y^2=4\).
Our idea is to find the maximum of \(f(x,y)\) by asking the following sequence of questions:
\(1^{\circ}\) Is the number 0 the maximum?
\(2^{\circ}\) Is the number 1 the maximum?
\(3^{\circ}\) Is the number 0.059 the maximum?
\(4^{\circ}\) Is the number -11 the maximum?
\(5^{\circ}\) How about 17?
It seems foolish to hope to answer all these questions. Honestly, it is impossible even to ask all these questions, but let us ignore the reality for a moment. We will answer the above questions by asking easier questions:
\(1^{\circ}\) Can 0 be a value of the function?
\(2^{\circ}\) Can 1 be a value of the function?
\(3^{\circ}\) Can 0.059 be a value of the function?
\(4^{\circ}\) Can -11 be a value of the function?
\(5^{\circ}\) Can 17 be a value of the function?
Then we’ll look at all positive answers and circle out the smallest one, and that’s our minimum.
The last set of questions can be rephrased using geometrical language:
\(1^{\circ}\) Does the level curve \(f(x,y)=0\) intersect the curve \(x^2+y^2=4\)?
\(2^{\circ}\) Does the level curve \(f(x,y)=1\) intersect the curve \(x^2+y^2=4\)?
\(3^{\circ}\) Does the level curve \(f(x,y)=0.059\) intersect the curve \(x^2+y^2=4\)?
\(4^{\circ}\) Does the level curve \(f(x,y)=-17\) intersect the curve \(x^2+y^2=4\)?
\(5^{\circ}\) Does the level curve \(f(x,y)=17\) intersect the curve \(x^2+y^2=4\)?
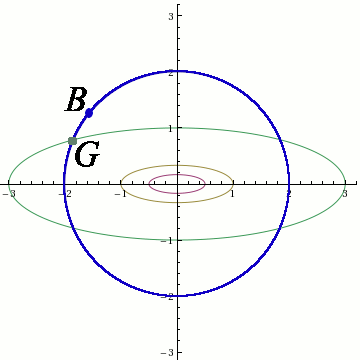
The above picture contains the blue circle \(x^2+y^2=4\) and several level curves. The level curves are from smallest to largest: \(\frac{x^2}9+y^2=\frac14\), \(\frac{x^2}9+y^2=1\), and \(\frac{x^2}9+y^2=3\). The first two do not intersect the surface hence \(\frac14\) and \(1\) are not candidates for the maximum.
Let us analyse the curve \[\frac{x^2}9+y^2=3.\] This curve is green and it intersects the blue circle in four points. One of them is prominently displayed with a big green dot and denoted by \(G\). The value of the function \(f\) at \(G\) is equal to \(3\).
However, this \(G\) has no chance of being the maximum. There is a blue point \(B\) that is on the circle and that is outside of this level curve. By being outside of it means that the value of \(f\) at the point \(B\) satisfies \(f(B)\neq f(G)\). There is a point \(B^{\prime}\) inside the curve \(\frac{x^2}9+y^2=3\) that also belongs to \(x^2+y^2=4\) such that \(f(B^{\prime})\neq f(G)\). We know that one of the numbers \(f(B)\) and \(f(B^{\prime})\) is larger than \(f(G)\) (in this particular example we can prove that it is \(B\)), hence \(G\) can’t be the maximizer.
We see that the maximizer can be attained only at the points were a level curve is tangent to \(x^2+y^2=4\).
Two curves are tangent when their normal vectors are parallel. The normal vector of the curve \(f(x,y)=c\) at the point \((x_0,y_0)\) is equal to \(\nabla f(x_0,y_0)\). Thus the candidates for minima and maxima of \(f\) are those points of \(x^2+y^2=4\) for which \(\nabla f\| \langle 2x,2y\rangle\).
Two vectors are parallel if and only if one of them is a multiple of the other. In other words, \(\nabla f\|\langle 2x,2y\rangle\) if there exists \(\lambda\neq 0\) such that \(\frac{2x}9=\lambda 2x\) and \(2u=\lambda 2y\). In summary, we are looking for the points \((x,y)\) that satisfy the following system of equations:
\[x^2+y^2=4\]
\[\frac{2x}9=\lambda\cdot 2x\]
\[2y=\lambda \cdot 2y.\]
From the third equation we conclude that \(y=0\) or \(\lambda = 1\). In the first case we get \(x=\pm 2\) and we get two candidates for extrema: \((2,0)\) and \((-2,0)\).
If \(\lambda =1\) then the second equation implies that \(x=0\). From the first one we obtain \(y=\pm 2\), and the candidates are \((0,2)\) and \((0,-2)\). Out of these four points we verify that \(f(2,0)=f(-2,0)=\frac49\) and \(f(0,2)=f(0,-2)=4\). This means that the maximum of \(f\) is \(4\) and is attained for \((x,y)\in\{(0,2), (0,-2)\}\). Similarly, the minimum is \(\frac49\) and is attained for \((x,y)\in\{(2,0),(-2,0)\}\).
The method of Lagrange multipliers
The proof of the following theorem can be completed using the idea of the previous section:
Lagrange multipliers
Assume that \(f(x,y)\) and \(g(x,y)\) are continuously differentiable functions. If the maximum or minimum of the function \(f\) under the condition \(g(x,y)=0\) occurs at a point \((x_0,y_0)\) for which \(\nabla g(x_0,y_0)\neq 0\), then there exists a constant \(\lambda\) such that \[\nabla f(x_0,y_0)=\lambda \nabla g(x_0,y_0).\]
Let us now solve Example 1.
Example 1.
Find the points \((x,y)\) on the curve \(x^2+y^2=1\) for which the quantity \(f(x,y)=xy\) is maximal.
Denote \(g(x,y)=x^2+y^2-1\). The candidates for the extremal values are the points for which \(\nabla g(x,y)=0\) and the solutions to the system:
\[f_x=\lambda g_x\]
\[f_y=\lambda g_y\]
\[g(x,y)=0.\]
Since \(\nabla g=\langle 2x,2y\rangle\) and \(\nabla f=\langle y,x\rangle\), we first see that the only solution to \(\nabla g(x,y)=0\) is \((x,y)=(0,0)\) which does not satisfy \(g(x,y)=0\). Hence the critical points are solutions of the system:
\[y=2\lambda x\]
\[x=2\lambda y\]
\[x^2+y^2=1.\]
Substituting the second equation in the first one yields \(y=4\lambda^2y\). Hence either \(y=0\) or \(\lambda^2=\frac14\). If the former is the case, then from the last equation we get solutions \(x=\pm 1\) which is not consistent with the second equation. Therefore \(y\neq 0\) and \(\lambda=\pm \frac12\).
-
Case 1. Assume that \(\lambda=\frac12\). Then the first equation implies that \(y=x\). The third equation gives \(x=y=\pm\frac1{\sqrt 2}\) and we get two candidates \((x,y)\in\left\{\left(\frac1{\sqrt 2},\frac1{\sqrt2}\right), \left(-\frac1{\sqrt 2},-\frac1{\sqrt 2}\right)\right\}\).
- Case 2. In this case we assume that \(\lambda=-\frac 12\). Then we get \(y=-x\) and from the equation \(x^2+y^2=1\) we get \((x,y)\in\left\{\left(-\frac1{\sqrt 2},\frac1{\sqrt2}\right), \left(-\frac1{\sqrt 2},\frac1{\sqrt 2}\right)\right\}\).
It is easy to check that \[f\left(\frac1{\sqrt 2},\frac1{\sqrt 2}\right)=f\left(-\frac1{\sqrt 2},-\frac1{\sqrt 2}\right)=\frac12\;\;\;\mbox{ and }\;\;\;
f\left(-\frac1{\sqrt 2},\frac1{\sqrt 2}\right)=f\left(\frac1{\sqrt 2},-\frac1{\sqrt 2}\right)=-\frac12.\]
Therefore the maximum of \(f\) is \(\frac12\) and the minimum is \(-\frac12\).
Example 2.
Let \(S\) be the surface given by the equation \[(2+x-y)^2+(z-x)^2+(z+y)^2=1.\]
Find the point on \(S\) whose distance from the \(z\)-axis is maximal.
The distance from the \(z\)-axis of the point \((x,y,z)\) is \(\sqrt{x^2+y^2}\). Hence we need to find the maximum of the function \(f(x,y,z)=x^2+y^2\) under the constraint \(g(x,y,z)=0\) where
\(g(x,y,z)=(2+x-y)^2+(z-x)^2+(z+y)^2-1\). We will solve this problem using the method of Lagrange multipliers.
We first need to find the critical points of the function \(f\) under the condition \(g(x,y,z)=0\). The critical points are those points on \(g(x,y,z)=1\) for which \(\nabla g=0\) or \(\nabla f\|\nabla g\).
We have \(\nabla f=\langle 2x,2y,0\rangle\) and \(\nabla g=\langle 2(2+x-y)+2(x-z),
2(y-x-2)+2(y+z), 2z-x+y\rangle\). The critical points are those \((x,y,z)\) for which either \(\nabla g(x,y,z)=0\) or there exists \(\lambda\) such that
\(g(x,y,z)=0\) and \(\lambda \nabla g (x,y,z)=\nabla f(x,y,z)\).
If \(\nabla g(x,y,z)=0\) then we must have \(2+2x-y-z=0\), \(2y-x-2+z=0\), and \(2z-x+y=0\). Adding the first two equations yields \(x+y=0\) and the third now implies \(z=x\). The first equation gives
\(2+2x=0\) hence \(x=-1\), \(y=1\), \(z=-1\). The point \((-1,1,-1)\) satisfies the required condition, hence it is a critical point.
The critical points are the solutions of the system:
\begin{eqnarray*}
\lambda(2+2x-y-z)&=& x\\
\lambda(2y-x-2+z)&=&y\\
2z-x+y&=&0\\
(2+x-y)^2+(z-x)^2+(z+y)^2&=&1.
\end{eqnarray*}
Adding the first two equations yields \(\lambda(x+y)=(x+y)\), or equivalently, \((x+y)(\lambda-1)=0\). Let us consider the following two cases:
Case 1. \(x+y=0\). Then we have \(y=-x\). The third equation yields \(2z=2x\) which implies \(z=x=-y\). The last equation now implies \((2+2x)^2=1\), which is equivalent to \(2+2x=\pm 1\) and the \(x\)-coordinates of the the critical points are the solutions of \(2+2x=1\) and \(2+2x=-1\). The first equation implies that \(x=-\frac12\) and the second implies that \(x=-\frac32\). The critical points are \(\left(-\frac12, \frac12,-\frac12\right)\) and \(\left(-\frac32,\frac32,-\frac32\right)\).
Case 2.
\(\lambda=1\). In this case the system becomes:
\begin{eqnarray*}
2+x-y-z&=&0\\
2z-x+y&=&0\\
(2+x-y)^2+(z-x)^2+(z+y)^2&=&1.
\end{eqnarray*}
The first two equations imply that \(z=-2\) and \(y-x=4\).
The last equation now becomes \(4+(-2-x)^2+(-2+x+4)^2=1\) which is equivalent to
\[4+2(2+x)^2=1.\] This equation has no solutions.
Therefore the maximum is attained for the point \(\left(-\frac32,\frac32,-\frac32\right)\) and its distance from the \(z\)-axis is \(3\sqrt 2\).
Practice problems
Problem 1. Find the maximal value of the function \(f(x,y,z)=xy+yz+zx\), if \(x\), \(y\), and \(z\) are real numbers that satisfy \(x^2+y^2+z^2=1\)
This problem can be solved without using Lagrange multipliers. Notice that
\[f(x,y,z)=x^2+y^2+z^2-\frac{(x-y)^2+(y-z)^2+(z-x)^2}2\] \[=1-\frac{(x-y)^2+(y-z)^2+(z-x)^2}2\leq 1.\]
The maximum is attained when \(x=y=z\) which happens for \((x,y,z)=\left(\frac1{\sqrt 3},\frac1{\sqrt 3},\frac1{\sqrt 3}\right)\).
Problem 2. Find the minimal area of the ellipse of the form \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) that encloses the circle \(x^2+y^2=2y\).
We may assume that \(a> 0\) and \(b> 0\). The volume of the ellipse is \(ab\pi\). Hence we want to find the minimum of the function \(f(a,b)=ab\pi\) under the condition that
the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) encloses the circle \(x^2+y^2=2y\). This is a problem where we will use Lagrange multipliers, but we first
have to transform the constraints in the form \(g(a,b)=0\). So far the constraints are in an unpleasant geometrical form. There is some work to be done.
Hence, our first goal is to understand what does it mean for the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) to enclose the circle \(x^2+y^2=2y\).
This can be seen in the following way: Each point on the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) is outside of the circle
\(x^2+y^2=2y\) This is still not in the satisfactory form \(g(a,b)=0\) but we are slowly getting there.
Our constraint can be further understood as Each point of the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) satisfies \(x^2+y^2-2y\geq 0\),
or If \((x,y)\) satisfies \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) then \(x^2+y^2-2y\geq 0\), or
\(\min\{x^2+y^2-2y\}\geq 0\) under the condition \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\).
We will now use Lagrange multipliers to find the minimum of \(M(x,y)=x^2+y^2-2y\) under the condition \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\). This minimum will
be a function of \(a\) and \(b\). Then we will require
that minimum to be \(0\) in order to find the conditions on \(a\) and \(b\) that are necessary for the ellipse to enclose the circle.
Now we have the system:
\[
2x=\frac{2\lambda x}{a^2}\]
\[2y-2=\frac{2\lambda y}{b^2}\]
\[\frac{x^2}{a^2}+\frac{y^2}{b^2}=1.\]
From the first equation we arrive to the following two cases \(x=0\) and \(x\neq 0\):
\(1^{\circ}\) \(x=0\). From the last equation (the equation of the ellipse) we conclude that \(y=b\) or \(y=-b\). Our candidates are \((0,b)\) and \((0,-b)\).
\(2^{\circ}\) \(x\neq 0\). The first equation now becomes \(\lambda={a^2}\). We can now place this value of \(\lambda\) in the second equation. The equation
becomes \(y\cdot(1-\frac{a^2}{b^2})=1\). We now consider two cases:
\(2.1^{\circ}\) \(a^2=b^2\). Then this equation doesn’t have a solution for \(y\).
\(2.2^{\circ}\) \(a^2\neq b^2\). We can solve for \(y\): \(y=\frac{b^2}{b^2-a^2}\). Solving for \(x\) from the third equation gives us:
\(x^2=\frac{a^2((b^2-a^2)^2-b^2)}{(b^2-a^2)^2}\). Therefore the critical points are
\[(x,y)\in\left\{\left(+\sqrt{\frac{a^2((b^2-a^2)^2-b^2)}{(b^2-a^2)^2}},\frac{b^2}{b^2-a^2}\right),
\left(-\sqrt{\frac{a^2((b^2-a^2)^2-b^2)}{(b^2-a^2)^2}},\frac{b^2}{b^2-a^2}\right)\right\}.\]
All critical points are \[(x,y)\in\left\{\left(+\sqrt{\frac{a^2((b^2-a^2)^2-b^2)}{(b^2-a^2)^2}},\frac{b^2}{b^2-a^2}\right),
\left(-\sqrt{\frac{a^2((b^2-a^2)^2-b^2)}{(b^2-a^2)^2}},\frac{b^2}{b^2-a^2}\right),(0,b),(0,-b)\right\}.\]
Now we have \(M(0,\pm b)=b^2-2b\), and in the case \(a^2\neq b^2\):
\[
M\left(\pm\sqrt{\frac{a^2((b^2-a^2)^2-b^2)}{(b^2-a^2)^2}},\frac{b^2}{b^2-a^2}\right)=\frac{a^2(b^2-a^2)^2-a^2b^2+b^4-2b^4+2b^2a^2}
{(b^2-a^2)^2} \] \[=
\frac{a^2(b^2-a^2)^2-b^2(b^2-a^2)}
{(b^2-a^2)^2}\] \[
=\frac{a^2(b^2-a^2)-b^2}
{b^2-a^2}=\frac{a^2b^2-a^4-b^2}{b^2-a^2}.
\]
The minimum of \(M\) is the smaller of the numbers \(b^2-2b\) and \(\frac{a^2b^2-a^4-b^2}{b^2-a^2}\).
The smaller of these two numbers has to be \(\geq 0\). This means that both of the numbers have to be \(\geq 0\).
In particular we must have \(b^2-2b\geq 0\), or, equivalently \(b\geq 2\) (we have assumed that \(b> 0\)).
Now consider the two cases:
\(1^{\circ}\) \(a\geq b\). Then \(\frac{a^2b^2-a^4-b^2}{b^2-a^2}\geq 0\) because the denominator is negative, and
the numerator satisfies \(a^2b^2-a^4-b^2< a^2\cdot a^2-a^4-b^2=-b^2< 0\). Now the only condition is \(b\geq 2\). Turning back to the original
problem and using the fact \(a\geq b\) we see that the minimal ellipse is one for which \(a=b=2\). This ellipse happens to enclose the circle and its
area is \(4\pi\).
\(2^{\circ}\) \(a< b\). Then \(\frac{a^2b^2-a^4-b^2}{b^2-a^2}\geq 0\) is equivalent to
\(a^2b^2-a^4-b^2\geq 0\). Now the original problem is asking us to minimize the function
\(f(a,b)=ab\) under the condition \(g(a,b)=0\) where \(g(a,b)=a^2b^2-a^4-b^2\). The function \(f\) attains its minimum at the same points as \(h(a,b)=(f(a,b))^2\).
It is more convenient to minimize \(h(a,b)=a^2b^2\) under the condition \(g(a,b)=0\) because we can do the substitution \(\alpha=a^2\) and \(\beta=b^2\)
to transform the problem into minimizing \(h(\alpha,\beta)=\alpha\cdot\beta\) under the condition
\(\alpha\beta-\alpha^2-\beta=0\).
We use the Lagrange multipliers again:
\[
\beta=\mu(\beta-2\alpha)\]
\[
\alpha=\mu(\alpha-1)\]
\[\alpha\beta-\alpha^2-\beta=0.
\]
From the second equation we get that \(\alpha(1-\mu)=-1\). Consider the following two cases:
\(2.1^{\circ}\) \(\mu=1\). In this case the second equation becomes the impossible one. There are now critical points in this case.
\(2.2^{\circ}\) \(\mu\neq 1\). Then \(\alpha=\frac{1}{\mu-1}\). From the first equation we get
\(\beta=\frac{2\mu\alpha}{\mu-1}=\frac{2\mu^2}{(\mu-1)^2}\).
It is now convenient to notice that \(\beta=2\alpha^2\) and substitute this into the third equation to get:
\(2\alpha^3-\alpha^2-2\alpha^2=0\) and \(\alpha^2(2\alpha-3)=0\). We get \(\alpha=0\) or \(\alpha=\frac32\). Then our candidates are
\((\alpha,\beta)\in\left\{(0,0),\left(\frac32,\frac92\right)\right\}\).
Using our assumption \(a,b> 0\) we get that the only critical point of \(M\) is
\((a,b)=\left(\sqrt{\frac{3}2},\sqrt{\frac92}\right)\). The area of the ellipse is now equal to
\(\pi\cdot \frac{3\sqrt3}2\). Since \(\pi\frac{3\sqrt 3}2< 4\pi\) we get that the minimal area of the ellipse is \(\pi\cdot \frac{3\sqrt3}2\)
and it is attained when \(a=\sqrt{\frac32}\) and \(b=\frac3{\sqrt2}\).
Problem 3. Find the minimal distance from the origin attained by a point on the surface \(xyz=3\).
Define \(g(x,y,z)=xyz-3\). Our goal is to find the minimal value of the function \(f(x,y,z)=x^2+y^2+z^2\) in the set \[D=\left\{(x,y,z): g(x,y,z)=0\right\}.\]
Using the method of Lagrange multipliers, we will first find all the critical points \((x,y,z)\) of the function \(f\) in the set \(D\). The minimizing triple \((x,y,z)\) is among those critical points. _br__br_
Critical points are points at which the functions is not differentiable, the points at which the gradient of \(g\) is \(0\), and the points at which the vectors \(\nabla f\) and \(\nabla g\) are parallel. Since \(\nabla g=\langle yz, xz, xy\rangle\), we see that \(\nabla g\neq 0\) in \(D\). The functions \(f\) and \(g\) are differentiable on the entire \(\mathbb R^3\), hence the only critical points are those \((x,y,z)\) for which there exists \(\lambda\) such that \(\nabla f=\lambda \nabla g\). Together with \(g(x,y,z)=0\) this gives us the system of equations:
\[2x=\lambda yz\]
\[2y=\lambda xz\]
\[2z=\lambda xy\]
\[xyz=3.\]
If we multiply the first equation by \(x\) and the second by \(y\) and subtract the two obtained equations we get \(x^2=y^2\). Similarly we get \(y^2=z^2\) hence \(x^2=y^2=z^2\). Since \(f(x,y,z)=f(\pm x, \pm y, \pm z)\) it suffices to study only those critical points whose all three coordinates are positive.
Assuming that \(x, y, z\geq 0\) we now get \((x,y,z)=\left(\sqrt[3]3,\sqrt[3]3,\sqrt[3]3\right)\) is the only critical point with all three coordinates positive. We have that the minimal value of \(f\) is \(3\cdot 3^{2/3}\). This is the minimal value because we have \(f(x,y,z)\to\infty\) if one of \(x\), \(y\), \(z\) tends to \(\infty\).
Problem 4. Assume that the vertices of a hexagon \(ABCDEF\) lie on a circle \(x^2+y^2=1\) and are positioned in such a way that \(A\) and \(D\) are on the \(x\)-axis; \(B\) and \(F\) are symmetric with respect to the \(x\) axis; \(B\) and \(C\) are symmetric with respect to the \(y\)-axis; and \(C\) and \(E\) are symmetric with respect to the \(x\) axis. A solid of revolution \(S\) is generated by rotating the hexagon \(ABCDEF\) rotates around \(x\) axis. Find the maximal volume of the solid that can be obtained in this way.
Assume that coordinates of \(B\) are \((x,y)\) and that \(B\) is in the first quadrant. Now we can determine the coordinates of each of the vertices:
\[A(1,0),\;\; B(x,y),\;\; C(-x,y),\;\; D(-1,0),\;\; E(-x,-y),\;\; F(x,-y).\]
The required solid could be seen as the union of the cylinder \(Z\) obtained by rotating \(BCEF\) around \(x\)-axis and two cones \(C_1\) and \(C_2\) obtained by rotating the triangles \(ABF\) and \(CDE\). The radius of the cylinder is \(y\), and its height is \(2x\). Hence its volume is equal to \[V(Z)=y^2\cdot 2x\cdot\pi.\] The radius of each of the cones is equal to \(y\) and the height of each of them is \(1-x\), hence the volumes of \(C_1\) and \(C_2\) satisfy \[V(C_1)=V(C_2)=\frac13\cdot y^2\cdot (1-x)\cdot\pi.� \]
Therefore we want to maximize the function \[f(x,y)=2\pi y^2\cdot \left(x+\frac{1-x}3\right)=\frac{2}3\pi y^2(1+2x),\]
subject to the constraints \(x^2+y^2=1\) and \(x,y\geq 0\). Denote \(g(x,y)=x^2+y^2-1\). Let us find the critical points of the function \(f(x,y)\) under the constraint \(g(x,y)=0\). According to the theory of Lagrange multipliers, the critical points \((x,y)\) are those where one of the following condition is met:
\(1^{\circ}\) \(\nabla g=0\),
\(2^{\circ}\) \(\nabla f=0\),
\(3^{\circ}\) \(\nabla g\|\nabla f\),
\(4^{\circ}\) One of the functions \(f\) and \(g\) is not differentiable,
\(5^{\circ}\) \((x,y)\) is on the boundary.
We first consider the case \(5^{\circ}\).
The boundary points are \((x,y)\in\{(0,1),(1,0)\}\).
Both functions are differentiable, so there are no critical points in case \(4^{\circ}\).
Let us now find \(\nabla f\) and \(\nabla g\): \[\nabla g(x,y)=2\langle x,y\rangle\;\;\mbox{ and }\;\; \nabla f(x,y)=\frac{4\pi}3\langle y^2, y(1+2x)\rangle.\]
We see that \(\nabla g\neq 0\) under the condition \(g(x,y)=0\). The gradient \(\nabla f\) could be zero if \(y=0\), but that critical point is already accounted for since it is on the boundary (case \(5^{\circ}\)).
Therefore we only need to find the critical points for which \(\nabla f\) and \(\nabla g\) are parallel.
In order to do this, we look for \((x,y)\) such that \(g(x,y)=0\) and \(\nabla f(x,y)\|\nabla g(x,y)\). We obtain the system of equations:
\[2x=\lambda \cdot \frac{4\pi}{3}y^2\]
\[2y=\lambda \cdot \frac{4\pi}3 y(1+2x)\]
\[x^2+y^2=1.\]
Let us introduce the substitution \(\mu=\lambda\cdot \frac{2\pi}3\). Then the system becomes
\[x=\mu y^2\]
\[y=\mu y(1+2x)\]
\[x^2+y^2=1\]
Consider two cases: \(y=0\) and \(y\neq 0\). If \(y=0\), then the first equation would imply that \(x=0\), and the last equation cannot hold. If \(y\neq 0\), then the second equation implies \(1=\mu\cdot (1+2x)\). Multiplying the first equation by \((1+2x)\) and using that \(\mu(1+2x)=1\) we get: \(x(1+2x)= y^2\). The last equation now implies \[x^2+x(1+2x)=1\] which is equivalent to \(3x^2+x-1=0\). This last equation has two solutions \(x_1=\frac{-1+\sqrt{13}}{6}\) and \(x_2=\frac{-1-\sqrt{13}}6\). The solution \(x_2\) is negative, so we won’t consider it because of our assumption \(x\geq 0\).
From \(x=\frac{\sqrt{13}-1}6\) we now conclude that \[y^2=1-x^2=
\frac{36-1-13+2\sqrt{13}}{36}=\frac{22+2\sqrt{ 13}}{36}.\] Our assumption \(y\geq 0\) implies that
\[y=\left(\frac{22+2\sqrt {13}}{36}\right)^{1/2}\] and our critical point is \[(x,y)=\left(\frac{-1+\sqrt{13}}{6},
\left(\frac{22+2\sqrt {13}}{36}\right)^{1/2}
\right).\]
Since \(f(1,0)=0\), \(f(0,1)= \frac{2\pi}3\) and \[f\left(\frac{-1+\sqrt{13}}{6},
\left(\frac{22+2\sqrt {13}}{36}\right)^{1/2}
\right)=\pi\cdot \frac{11+\sqrt{13}}{27}\cdot \frac{3-1+\sqrt{13}}3=\frac{35+23\sqrt{13}}{81}\pi.\]
the maximal volume is \(\frac{35+23\sqrt{13}}{81}\pi\).
Problem 5. Find the minimal value of the function \(f(x,y)=x^2+y^2+z^2\) if \(x\), \(y\), and \(z\) are real numbers that satisfy \(xyz^2=1\).
Define \(g(x,y,z)=xyz^2-1\). Our goal is to find the minimal value of the function \(f(x,y,z)=x^2+y^2+z^2\) in the set \[D=\left\{(x,y,z): xyz^2=1\right\}.\]
Using the method of Lagrange multipliers, we will first find all the critical points \((x,y,z)\) of the function \(f\) in the set \(D\). The minimizing triple \((x,y,z)\) is among those critical points.
Critical points are points at which the functions is not differentiable, the points at which the gradient of \(g\) is \(0\), and the points at which the vectors \(\nabla f\) and \(\nabla g\) are parallel. Since \(\nabla g=\langle yz^2, xz^2, 2xyz\rangle\), we see that \(\nabla g\neq 0\) in \(D\). The functions \(f\) and \(g\) are differentiable on the entire \(\mathbb R^3\), hence the only critical points are those \((x,y,z)\) for which there exists \(\lambda\) such that \(\nabla f=\lambda \nabla g\). Together with \(g(x,y,z)=0\) this gives us the system of equations:
\[2x=\lambda yz^2\]
\[2y=\lambda xz^2\]
\[2z=\lambda 2xyz\]
\[xyz^2=1.\]
If we multiply the first equation by \(x\) and the second by \(y\) and subtract the two obtained equations we get \(x^2=y^2\). We can divide the third equation by \(2z\) since \(z\neq 0\) and conclude that \(\lambda xy=1\).
\(1^{\circ}\) Assume first that \(x=y\). Then we get \(\lambda> 0\) and \(x=y=\pm\frac1{\sqrt \lambda}\). Then the first equation implies \(z=\pm\sqrt {\frac2{\lambda}}\) and the equation \(g(x,y,z)=0\) now implies that \(\lambda=\sqrt 2\). Then the set of critical points is \[C=\left\{\left(\frac1{\sqrt[4] 2},\frac1{\sqrt[4]2}, {\sqrt[4] 2}\right),
\left(\frac1{\sqrt[4] 2},\frac1{\sqrt[4]2}, -{\sqrt[4] 2}\right), \left(-\frac1{\sqrt[4] 2},-\frac1{\sqrt[4]2}, {\sqrt[4] 2}\right), \right.\] \[\left. \left(-\frac1{\sqrt[4] 2},-\frac1{\sqrt[4]2}, -\sqrt[4] 2\right)\right\}.\]
The value of the function \(f\) at any of these critical points in equal to \(2\sqrt 2\).
\(2^{\circ}\) Assume that \(x=-y\). The equation \(g(x,y,z)=0\) implies that \(-x^2z^2=1\) which is impossible.
In order to conclude that \(2\sqrt 2\) is the absolute minimum, we need to notice that the function is bounded below by \(0\) hence it must attain the minimum.
Therefore the minimal value of \(f\) is equal to \(2\sqrt 2\).
