| 1. | Sets |
| 2. | Functions |
| 3. | Introduction to counting |
| 4. | Counting with bijections |
| 5. | Generating functions |
| 6. | Theory of generating functions (Milan Novaković) |
| 7. | Burnside's lemma |
| 8. | Polya's theorem |
Functions
Introduction
We will use Cartesian product of sets to define functions in an elegant way. To make things easier to understand, we will start by examples of functions and point out the most important properties that the function must satisfy.
We can think of a function as a rule. To each input value we assign exactly one output value according to this rule.
Example 1
Consider the function \(h:\mathbb N\to\mathbb Z\) defined in the following way: \[h(x)=x-17.\]
This is a function that takes a positive integer as an input and produces an integer as an output. If the input is \(22\) then we write \(h(22)=5\). Let us evaluate this function for several more inputs: \(h(37)=20\), \(h(100)=83\), \(h(3)=-14\). We can represent this graphically as:
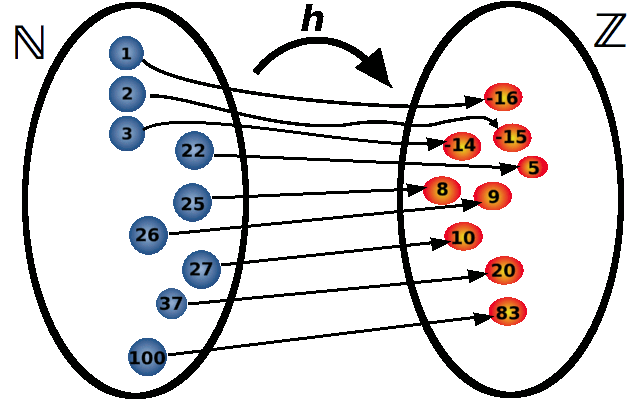
Another way to represent a function is by ordered pairs: \[(1,-16), (2,-15), (3,-14), \dots, (25,8), (26,9), (27,10), \dots\] The first number in the pair is the input, while the second is the corresponding output. This list of ordered pairs uniquely represents our function \(h\).
Example 2
Consider the following function \(g:\mathbb N^2\to\mathbb N\): \[g(x,y)=x+y.\]
This function takes an element of \(\mathbb N^2\). Elements of \(\mathbb N^2\) are ordered pairs of positive integer. To each positive integer this function assigns its sum. Thus we have \(g(3,17)=20\), \(g(17,17)=34\), \(g(11,96)=107\), etc.
We can again write our function \(g\) in a similar way as we did before:
\[\big((1,1),2\big), \big((1,2),3\big), \big((1,3),4\big), \big((1,4),5\big),\dots \]
\[\big((2,1),3\big), \big((2,2),4\big), \big((2,3),5\big), \big((2,4),6\big),\dots \]
\[\big((3,1),4\big), \big((3,2),5\big), \big((3,3),6\big), \big((3,4),7\big),\dots \]
\[ \dots\dots\dots\]
Consider the first element in the list: \(\big ((1,1),2\big)\). This is one ordered pair. Its second component is 2. Its first component is another ordered pair: \((1,1)\). The entire thing \(\big ((1,1),2\big)\) means that if the input is \((1,1)\) the output is \(2\).
Definition
The set \(X\) is called domain of function. The set \(Y\) is called co-domain (or range).
Every function is given by its domain, co-domain, and some rule describing how elements from domain are mapped to the co-domain.
Image and pre-image of a function
Assume that \(f:X\to Y\) is a function.Assume that \(A\subseteq X\). We define the image of \(A\) (and denote it by \(f(A)\)) in the following way: \[f(A)=\left\{ f(x): x\in A\right\}.\]
Consider the function \(h\) from Example 1. Then we have \[h\left(\{3,25\}\right)=\{-14,8\}, h\left(\{5,17,35\}\right)=\{-12,0,18\}.\]
Assume that \(B\subseteq Y\). We define the pre-image of \(B\) (and denote it by \(f^{-1}(B)\) as the set of all elements from \(X\) that get mapped to \(B\). The precise definition is the following: \[f^{-1}(B)=\left\{x\in X: f(x)\in B\right\}.\]
Again, consider the function \(h\) from Example 1. \[h^{-1}\left(\{7,8,11)\}\right)=\{24,25,38\},\;\; h^{-1}\left(\{-5\}\right)=\{12\},\;\; h^{-1}\left(\{-33\}\right)=\emptyset.\]
The experience has shown that you have a better chance of remembering the following theorem if it is stated in a rather unconventional way, as a multiple-choice question.
(A) \(f(P \cup Q)=f(P)\cup f(Q)\).
(B) \(f(P\cap Q)=f(P)\cap f(Q)\).
(C) \(f^{-1}(P \cup Q)=f^{-1}(P)\cup f^{-1}(Q)\).
(D) \(f^{-1}(P\cap Q)=f^{-1}(P)\cap f^{-1}(Q)\).
Injective, surjective, and bijective functions
In other words no two different values from \(X\) are mapped to the same value in \(Y\).
Composition of functions
Assume that \(f:X\to Y\) and \(g:Y\to Z\) are two functions. We define their composition \(g\circ f\) as a function \(g\circ f:X\to Z\) in the following way: For \(x\in X\) we have: \[g\circ f(x)= g\big(f(x)\big).\](a) If \(f\) and \(g\) are injective, then so is \(g\circ f\);
(b) If \(f\) and \(g\) are surjective, then \(g\circ f\) is surjective;
(c) If \(g\circ f\) is injective, then \(f\) is injective;
(d) If \(g\circ f\) is surjective, then \(g\) is surjective.
If a function \(f:X\to Y\) is bijective then it has an inverse. In other words, there exists a bijective function \(g:Y\to X\) such that \( g(f(x))=x\) for all \(x\in X\). Then we have \(g(f(y))=y\) for all \(y\in Y\).
The inverse of a function is denoted by \(f^{-1}\).
You may have noticed that the symbol \(f^{-1}\) is already used in this page. We used it to denote the pre-image of a set. Pre-image of the set exists always, while the inverse is a privilege of bijective functions only. From the context it is usually clear what we mean when we write \(f^{-1}(\) something\()\). For example, if that ``something’’ is a set, we mean the pre-image. If it is a number we are talking about inverse function.