Derivatives
Rate of Change
Consider the function \(f(x)=3x+7\). We have that \(f(5)=3\cdot 5+7=22\). The input value is \(5\), and the output is \(22\). If we increase the input by \(2\), it becomes \(7\) and the output becomes \(28\). This means if the input increases by \(2\), the output increases by \(6\).
Assume now that the original input is increased by \(12\). It becomes \(17\). The output is \(f(17)=3\cdot 17+7=58\), which is by \(36\) bigger than the original output.
In general, if the input is increased by value \(t\), the output increases by \(3\cdot t\), and this number \(3\) is called the rate of change.
We can study only the rate of change of a function. Let us consider the following example
Example 1
Consider the function \(f(x)=5x+1\). Find the rate of change of \(f\).
Assume that the value of the argument \(x\) of the function \(f\) is changed by \(\Delta x\). If we denote the old value by \(x_O\), the new one is \(x_N=x_O+\Delta x\). We now have
\[f(x_N)=5\cdot x_N+1=5\cdot (x_O+\Delta x)+1=5\cdot x_O+1+5\cdot \Delta x=f(x_O)+5\Delta x.\]
Therefore the change in \(f\) is equal to \(f(x_N)-f(x_O)=5\Delta x\) and the rate of change is equal to 5.
Now we may think that we are ready to define the rate of change for a general function. However, the following example is quite depressing. Consider the function \(g(x)=x^2\).
Let’s start with \(x_O=3\). We first find \(g(x_O)=9\). If we take \(x_N=4\), then \(g(x_N)=16\) and the change in \(g\) is \(\frac{16-9}{4-3}=7\) times bigger than the change in \(x\).
However, if we take \(x_{N^{\prime}}=5\) we get \(g(x_{N^{\prime}})=25\) and the change in \(g\) is \(\frac{25-9}{5-3}=8\) times bigger than the change in \(x\).
If we take \(x_{N^{\prime\prime}}=500\), then \(g(X_{N^{\prime\prime}})=250000\) and the change in \(g\) is \(\frac{250000-9}{500-3}=\frac{249999}{497}\) times bigger than the change in \(x\).
Despite this fact we are inclined to say that the rate of change of the function \(f(x)=x^2\) is small. This is because nobody cares about the difference between \(g(500)\) and \(g(3)\).
We are interested in the infinitesimal rate of change, and this is called a derivative of the function.
The definition
Definition of derivative
Assume that \(f\) is a function, and \(a\) a real number that belongs to the domain of definition of \(f\). If the limit \(\lim_{h\to 0}\frac{f(a+h)-f(a)}h\) exists, we say that the function \(f\) is differentiable at point \(a\) and we called the previous limit the derivative of \(f\) at point \(a\). We denote the derivative by \(f^{\prime}(a)\), i.e.:
\[f^{\prime}(a)=\lim_{h\to 0}\frac{f(a+h)-f(a)}h.\]
The slope of the tangent
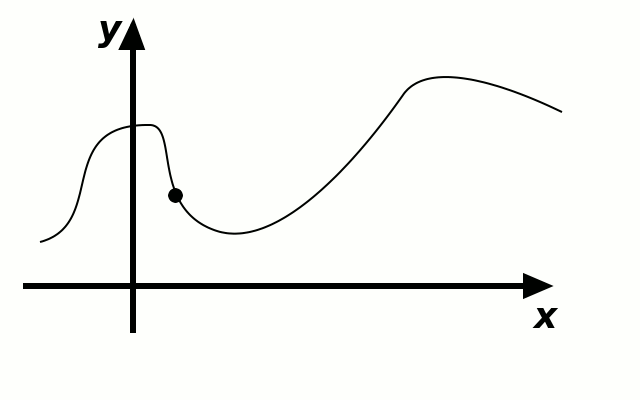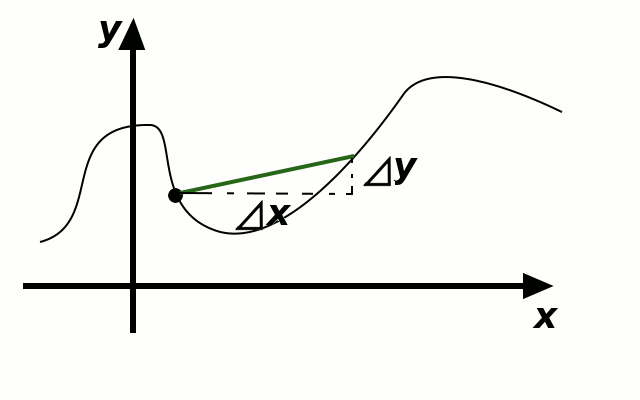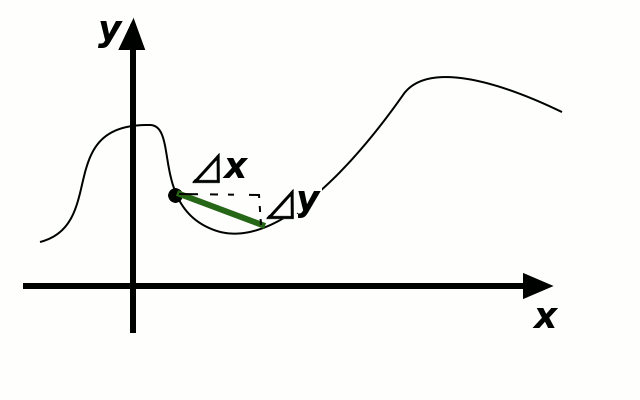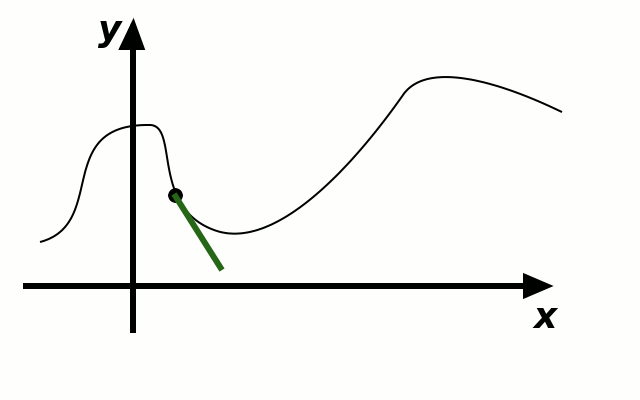
If we draw the graph of the function \(f\) in the \(xy\) plane, then the slope of the line between the points \((x,f(x))\) and \((x+\Delta x, f(x+\Delta x))\) is equal to \(\frac{f(x+\Delta x)-f(x)}{\Delta x}\).
As \(\Delta x\) gets smaller and smaller, the line between \((x,f(x))\) and \((x+\Delta x, f(x+\Delta x))\) becomes a more accurate approximation to the tangent line of the graph of \(f\). The quantity \[\lim_{\Delta x\to0}\frac{f(x+\Delta x)-f(x)}{\Delta x)}\] corresponds to the slope of the tangent line to the graph of \(f\) at the point \((x,f(x))\).
Derivatives of \(x^m\), \(e^x\), \(\sin x\), and \(\cos x\)
Our first theorem states that derivative of a constant function is \(0\).
Theorem (Derivative of a constant)Let \(C\) be arbitrary real number, and let \(f\) be the function defined as \(f(x)=C\) for all \(x\in\mathbb R\). Then \(f\) is differentiable for any \(a\in\mathbb R\) and \(f^{\prime}(a)=0\).
An easy calculation yields: \[\lim_{h\to 0}\frac{f(a+h)-f(a)}h=\lim_{h\to0}\frac{C-C}{h}=0.\] Therefore \(f^{\prime}(a)\) exists and is equal to \(0\).
Our next theorem states that the derivative of a function of the form \(f(x)=x^m\) is \(f^{\prime}(x)=mx^{m-1}\) if \(m\) is a positive integer.
Theorem (Power rule)
Let \(m\in\mathbb N\) and let \(f(x)=x^m\). Then \(f^{\prime}(a)=ma^{m-1}\) for all \(a\in\mathbb R\).
We can use the binomial formula to obtain: \[\lim_{h\to0} \frac{f(a+h)-f(a)}{h}=\lim_{h\to 0}\frac{(a+h)^m-a^m}{h}=
\lim_{h\to 0}\frac{a^m+\binom m1 a^{m-1}\cdot h+\binom m2a^{m-2}h^2+\cdots + h^m-a^m}{h}\]
\[\Rightarrow f^{\prime}(a)=ma^{m-1}+\lim_{h\to 0}\left( \binom m2a^{m-2}h+\binom m3a^{m-3}h^2+\cdots + h^{m-1}\right)=ma^{m-1}.\]
The power rule holds even for \(m\in\mathbb R\), but the proof is more complicated, and we will omit it for now.
Theorem (General power rule)
Let \(m\in\mathbb R\) and let \(f(x)=x^m\). Then \(f^{\prime}(a)=ma^{m-1}\) for all \(a\in\mathbb R\).
Theorem (Derivative of the exponential function) If \(f(x)=e^x\), then \(f^{\prime}(a)=e^a\) for every real number \(a\).
We will first prove that \(\lim_{h\to 0}\frac{e^h-1}h=1\).
The fundamental property of the number \(e\) is: \[\left(1+\frac1 n\right)^{n} < e < \left(1+\frac1{n-1}\right)^{n}\;\;\;\mbox{for all positive integers } n > 1.\quad\quad\quad\quad\quad (\star)\]
Assume first that \(h > 0\). If we raise the first inequality to the power \(h\) we get \(\left(1+\frac1n \right)^{nh} < e^h\), and Bernoulli’s inequality now gives: \[e^h > \left(1+\frac1n \right)^{nh} > 1+h \;\;\;\Rightarrow \;\;\; \frac{e^h-1}h > 1.\]
Consider now the second inequality in \((\star)\) and also raise it to the power \(h\). We obtain:
\[e^h < \left( \frac{n}{n-1}\right)^{nh}\;\;\;\Leftrightarrow
e^{-h} > \left(1-\frac1n\right)^{nh} > 1-h.\]
In the last step we used Bernoulli’s inequality. This implies that \(1 > e^h-he^h\) which is equivalent to \(\frac{e^h-1}h < e^h\).
Therefore, by squeeze theorem we have \[\lim_{h\to0+}\frac{e^h-1}h=1.\] If \(h < 0\) we have \[\lim_{h\to0-}\frac{e^h-1}h=-\lim_{h\to 0-}e^h\cdot \lim_{h\to 0-}\frac{1-e^{-h}}{-h}=-\lim_{h\to 0-}e^h\cdot \lim_{s\to 0+}\frac{1-e^s}{s}=1.\]
Now we have that \[\lim_{h\to0}\frac{f(a+h)-f(a)}h=\lim_{h\to0}\frac{e^{a+h}-e^a}h=e^a\lim_{h\to 0}\frac{e^h-1}h=e^a.\]
Theorem (Derivatives of \(\sin\) and \(\cos\)) If \(f(x)=\sin x\), then \(f^{\prime}(a)=-\cos a\) for every real number \(a\). If \(g(x)=\cos x\), then \(g^{\prime}(a)=-\sin a\).
We will use the identities \[\lim_{x\to 0}\frac{\sin x}{x}=1\quad\quad\quad \mbox{and} \quad\quad\quad \lim_{x\to0}\frac{1-\cos x}{x^2}=\frac12.\]
We now have \[\lim_{h\to 0}\frac{\sin(a+h)-\sin a}{h}=\lim_{h\to 0}\frac{\sin a\cos h+\cos a\sin h-\sin a}h=\sin a\lim_{h\to 0}\frac{\cos h-1}h+\cos a\lim_{h\to 0}\frac{\sin h}h=\cos a.\]
Similarly, \[\lim_{h\to0}\frac{\cos(a+h)-\cos a}h=\lim_{h\to 0}\frac{\cos a\cos h-\sin a \sin h-\cos a}h = \cos a\lim_{h\to 0}\frac{\cos h-1}h-\sin a\lim_{h\to 0}\frac{\sin h}h=-\sin a.\]
Practice Problems
Problem 1. Let \(g(x)=\cos x\). Find \(g'(x)\).
The result is \(g'(x)=-\sin x\).
Problem 2. Let \(f(x)=x^3\). Find \(f'(4)\).
We first find \(f'(x)=3x^2\). Now we substitute \(x=4\) and obtain \(f'(4)=3\cdot 4^2=48\).
Problem 3. Let \(f(x)=x^3\). Find \(f'(4)\).
We first find \(f'(x)=3x^2\). Now we substitute \(x=4\) and obtain \(f'(4)=3\cdot 4^2=48\).
Problem 4 The definition of the derivative \(f^{\prime}(a)\) of a function \(f\) at a point \(a\) states that \[f^{\prime}(a)=\lim_{h\to0}\frac{f(a+h)-f(a)}h.\] This definition is equivalent to:
- (A) \(\displaystyle f^{\prime}(a)=\lim_{a\to 0}\frac{f(a+h)-f(a)}h\)
- (B) \(\displaystyle f^{\prime}(a)=\lim_{x\to a}\frac{f(a)-f(x)}x\)
- (C) \(\displaystyle f^{\prime}(a)=\lim_{x\to a}\frac{f(a)-f(x)}a\)
- (D) \(\displaystyle f^{\prime}(a)=\lim_{x\to a}\frac{f(a)-f(x)}{a-x}\)
- (E) \(\displaystyle f^{\prime}(a)=\lim_{x\to a}\frac{f(x)-f(a)}{a-x}\)
The correct answer is D. Using the substitution \(x=a+h\), the given identity \(f^{\prime}(a)=\lim_{h\to 0}\frac{f(a+h)-f(a)}h\) becomes \[f^{\prime}(a)=\lim_{x\to a}\frac{f(x)-f(a)}{x-a}.\]
Problem 5. If \(f(x)=e^x\), find \(f^{\prime}(e)\).
Since \(f'(x)=e^x\), we have \(f^{\prime}(e)=e^e\).
