Maximum and Minimum of a Function
Local maximum and minimum
Consider the function \(f(x)=x^4-2x^2+1\). Without using too much theory we can express \(f\) in the following way: \[f(x)=\left(x^2-1\right)^2=(x-1)^2\cdot (x+1)^2.\] From this expression we see that the function is always non-negative and its minimum \(0\) is attained at \(2\) points: \(-1\) and \(1\). On the real line, the function does not have maximum, because as \(x\) approaches infinity, the value of \(f\) goes to infinity.
Let us now take a look at the graph of the function \(f\):
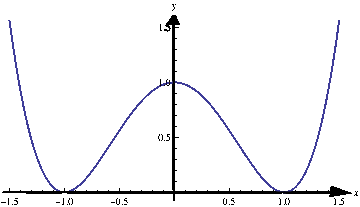
The graph shows that the minimum is \(0\) at two points: \(-1\) and \(1\). However, the graph shows that the point \(x=0\) is special: the function has a ``peak’’ at that point. It is not real maximum (because we saw that the function goes to \(+\infty\)). This point is called ``local maximum.’’ We are now going to define this term precisely.
In an analogous way we define the local minimum.
Application of differential calculus in finding the local extrema
Notice that the previous theorem makes sense: If \(f\) attains maximum or minimum at \(a\), the tangent has to be horizontal at \(a\), hence the slope is \(0\). The previous proof is just a formal way of writing this observation.