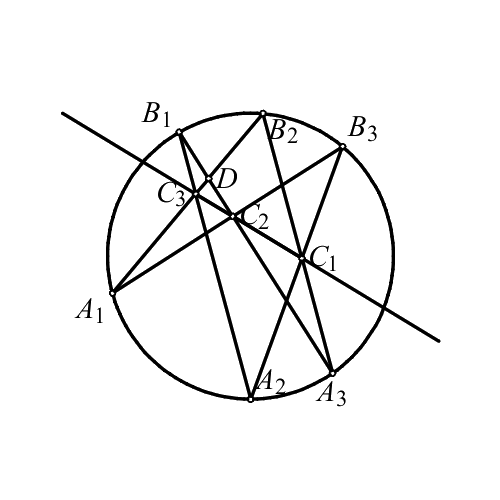| 1. | Cross ratio. Harmonic conjugates. Perspectivity. Projectivity |
| 2. | Desargue's theorem |
| 3. | Theorems of Pappus and Pascal |
| 4. | Pole. Polar. Theorems of Brianchon and Brokard |
| 5. | Problems |
Theorems of Pappus and Pascal
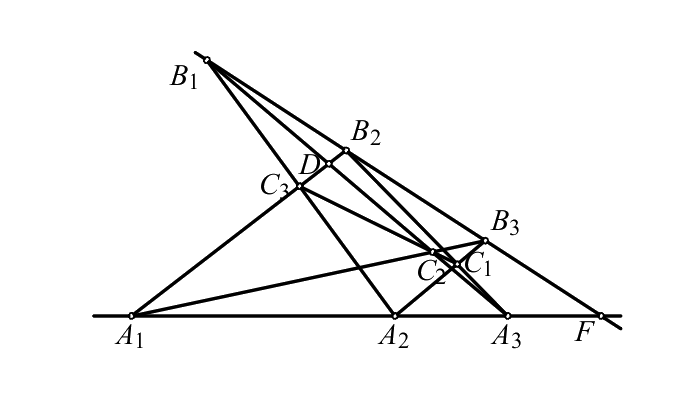
Theorem 4 (Pappus)
The points \(A_1\), \(A_2\), \(A_3\) belong to the line \(a\),
and the points \(B_1\), \(B_2\), \(B_3\) belong to the line \(b\).
Assume that
\(A_1B_2\cap A_2B_1=C_3\), \(A_1B_3\cap A_3B_1=C_2\),
\(A_2B_3\cap A_3B_2=C_1\). Then \(C_1\), \(C_2\), \(C_3\)
are colinear.
Theorem 5 (Pascal)
Assume that the points
\(A_1\), \(A_2\), \(A_3\), \(B_1\), \(B_2\), \(B_3\) belong to a
circle. The point in intersections of \(A_1B_2\) with \(A_2B_1\),
\(A_1B_3\) with \(A_3B_1\), \(A_2B_3\) with \(A_3B_2\)
lie on a line.