Problems in Projective Geometry

Let \(T=AC\cap BD\). Consider the sequence of the perspectivities \[PQRS\frac{A}{\overline\wedge} BDTS\frac{C}{\overline\wedge} QPRS.\] Since the perspectivity preserves the cross-ratio \(\mathcal R(P,Q;R,S)=\mathcal R(Q,P;R,S)\) we obtain that \(\mathcal H(P,Q;R,S)\).

Let \(\alpha=\angle BAC\), \(\beta=\angle CBA\), \(\gamma=\angle ACB\) and \(\varphi=\angle BAM\). Using the sine theorem on \(\triangle ABM\) and \(\triangle ACM\) we get \[\frac{BM}{MC}=\frac{BM}{AM}\frac{AM}{CM}= \frac{\sin\varphi}{\sin\beta}\,\frac{\sin\gamma}{\sin(\alpha- \varphi)}.\] Similarly using the sine theorem on \(\triangle ABN\) and \(\triangle ACN\) we get \[\frac{BN}{NC}=\frac{BN}{AN}\frac{AN}{CN}= \frac{\sin(90^\circ-\varphi)}{\sin(180^\circ-\beta)}\, \frac{\sin\gamma}{\sin(90^\circ+\alpha-\varphi)}.\] Combining the previous two equations we get \[\frac{BM}{MC}:\frac{BN}{NC}=\frac{\tan\varphi}{\tan(\alpha- \varphi)}.\] Hence, \(|\mathcal R(B,C;M,N)|=1\) is equivalent to \(\tan\varphi=\tan(\alpha-\varphi)\), i.e. to \(\varphi=\alpha/2\). Since \(B\neq C\) and \(M\neq N\), the relation \(|\mathcal R(B,C;M,N)|=1\) is equivalent to \(\mathcal R(B,C;M,N)=-1\), and the statement is now shown.

The motivation is the problem 1. Choose a point \(K\) outside \(AB\) and point \(L\) on \(AK\) different from \(A\) and \(K\). Let \(M=BL\cap CK\) and \(N=BK\cap AM\). Now let us construct a point \(D\) as \(D=AB\cap LN\). From the problem 1 we indeed have \(\mathcal H(A,B;C,D)\).

Let us denote \(D=AS\cap BC\). According to the problem 1 we have \(\mathcal H(R,S;A,D)\). Now we construct the point \(D=AS\cap BC\). We have the points \(A\), \(D\), and \(S\), hence according to the previous problem we can construct a point \(R\) such that \(\mathcal H(A,D;S,R)\). Now we construct \(P=BS\cap CR\) and \(Q=CS\cap BR\), which solves the problem.

It is well known (and is easy to prove using Ceva's theorem) that the lines \(AD\), \(BE\), and \(CF\) intersect at a point \(G\) (called a Gergonne point of \(\triangle ABC\)) Let \(X=BC\cap EF\). As in the problem 1 we have \(\mathcal H(B,C;D,X)\). If we denote \(X\prime =BC\cap PQ\) we analogously have \(\mathcal H(B,C;D,X\prime )\), hence \(X=X\prime \).

Let us denote \(x=KL\), \(y=LM\), \(z=MN\). We have to prove that \(x+y+z\ge 3y\), or equivalently \(x+z\ge 2y\). Since \(\mathcal R(K,N;L,M)=\mathcal R(B,C;D,E)\), we have \[\frac x{y+z}:\frac{x+y}z= \frac{\overrightarrow{KL}}{\overrightarrow{LN}}:\frac{\overrightarrow{KM}}{\overrightarrow{MN}}= \frac{\overrightarrow{BD}}{\overrightarrow{DC}}:\frac{\overrightarrow{BE}}{\overrightarrow{EC}}= \frac 12\cdot\frac 12,\] implying \(4xz=(x+y)(y+z)\).

If it were \(y > (x+z)/2\) we would have \[x+y > \frac 32 x+\frac 12 z=2\frac 14(x+x+x+z)\ge 2 \sqrt[4]{xxxz},\] and analogously \(y+z > 2\sqrt[4]{xzzz}\) as well as \((x+y)(y+z) > 4xz\) which is a contradiction. Hence the assumption \(y > (x+z)/2\) was false so we have \(y\le (x+z)/2\).

Let us analyze the case of equality. If \(y=(x+z)/2\), then \(4xz=(x+y)(x+z)=(3x+z)(x+3z)/4\), which is equivalent to \((x-z)^2=0\). Hence the equality holds if \(x=y=z\). We leave to the reader to prove that \(x=y=z\) is satisfied if and only if \(p\parallel BC\).

Let \(E=AB\cap CD\), \(F=AD\cap BC\). Consider the sequence of perspectivities \[ ABEM_1\frac{D}{\overline\wedge}FBCM_2\frac{A}{\overline\wedge}DECM_3\frac{B}{\overline\wedge} DAFM_4\frac{C}{\overline\wedge}EABM_5. \quad\quad\quad\quad\quad (1)\] According to the conditions given in the problem this sequence of perspectivities has two be applied three more times to arrive to the point \(M_{13}\). Notice that the given sequence of perspectivities maps \(A\) to \(E\), \(E\) to \(B\), and \(B\) to \(A\). Clearly if we apply (1) three times the points \(A\), \(B\), and \(E\) will be fixed while \(M_1\) will be mapped to \(M_{13}\). Thus \(M_1=M_{13}\).

Let \(X\prime \) be the point symmetric to \(Y\) with respect to \(P\). Notice that \[ \mathcal R(M,N;X,P) = \mathcal R(M,N;P,Y)\quad\mbox{(from } MNXP\frac{D}{\overline\wedge}MNAC\frac{B}{\overline\wedge}MNPY) \] \[ = \mathcal R(N,M;P,X\prime )\quad\mbox{( the reflection with the center }P\mbox{ preserves}\] \[ \qquad\qquad\qquad\quad\mbox{the ratio, hence it preserves the cross-ratio)} \] \[ = \frac{1}{\mathcal R(N,M;X\prime ,P)}=\mathcal R(M,N;X\prime ,P), \] where the last equality follows from the basic properties of the cross ratio. It follows that \(X=X\prime \).

Let \(J=DQ\cap BP\), \(K=EQ\cap CP\). If we prove that \(JK\parallel DE\) this would imply that the triangles \(BDJ\) and \(CEK\) are perspective with the respect to a center, hence with repsect to an axis as well (according to Desargue's theorem) which immediately implies that \(A\), \(P\), \(Q\) are colinear (we encourage the reader to verify this fact).

Now we will prove that \(JK\|DE\). Let us denote \(T=DE\cap PQ\). Applying the Menelaus theorem on the triangle \(DTQ\) and the line \(PF\) we get \[\frac{\overrightarrow{DJ}}{\overrightarrow{JQ}}\frac{\overrightarrow{QP}}{\overrightarrow{PT}}\frac{ \overrightarrow{TF}}{\overrightarrow{FD}}=-1.\] Similarly from the triangle \(ETQ\) and the line \(PG\): \[\frac{\overrightarrow{EK}}{\overrightarrow{KQ}}\frac{\overrightarrow{QP}}{\overrightarrow{PT}} \frac{\overrightarrow{TG}}{\overrightarrow{GE}}=-1.\] Dividing the last two equalities and using \(DT\cdot TG=FT\cdot TE\) (\(T\) is on the radical axis of the circumcircles of \(\triangle DPG\) and \(\triangle FPE\)), we get \[\frac{\overrightarrow{DJ}}{\overrightarrow{JQ}}=\frac{\overrightarrow{EK}}{\overrightarrow{KQ}}.\] Thus \(JK\parallel DE\), q.e.d.

Apply the inversion with the respect to \(I\). We leave to the reader to draw the inverse picture. Notice that the condition that \(I\) is the incentar now reads that the circumcircles \(A_i^*A_{i+1}^*I\) are of the same radii. Indeed if \(R\) is the radius of the circle of inversion and \(r\) the distance between \(I\) and \(XY\) then the radius of the circumcircle of \(\triangle IX^*Y^*\) is equal to \(R^2/r\). Now we use the following statement that is very easy to prove: ``Let \(k_1\), \(k_2\), \(k_3\) be three circles such that all pass through the same point \(I\), but no two of them are mutually tangent. Then the centers of these circles are colinear if and only if there exists another common point \(J\neq I\) of these three circles.\(\prime\prime\)

In the inverse picture this transforms into proving that the lines \(A_1^*B_1^*\), \(A_2^*B_2^*\), and \(A_3^*B_3^*\) intersect at a point.

In order to prove this it is enough to show that the corresponding sides of the triangles \(A_1^*A_2^*A_3^*\) and \(B_1^*B_2^*B_3^*\) are parallel (then these triangles would be perspective with respect to the infinitely far line). Afterwards the Desargue's theorem would imply that the triangles are perspective with respect to a center. Let \(P_i^*\) be the incenter of \(A_{i+1}^*A_{i+2}^*I\), and let \(Q_i^*\) be the foot of the perpendicular from \(I\) to \(P_{i+1}^*P_{i+2}^*\). It is easy to prove that \[\overrightarrow{A_1^*A_2^*}= 2\overrightarrow{Q_1^*Q_2^*}= -\overrightarrow{P_1^*P_2^*}.\] Also since the circles \(A_i^*A_{i+1}^*I\) are of the same radii, we have \(P_1^*P_2^*\parallel B_1^*B_2^*\), hence \(A_1^*A_2^*\parallel B_1^*B_2^*\).

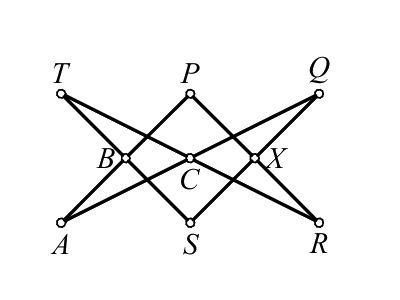
We will prove that the intersection \(X\) of \(PR\) and \(QS\) lies on the line \(BC\). Notice that the points \(P\), \(Q\), \(R\), \(S\) belong to the circle with center \(AT\). Consider the six points \(A\), \(S\), \(R\), \(T\), \(P\), \(Q\) that lie on a circle. Using Pascal's theorem with respect to the diagram we get that the points \(B\), \(C\), and \(X=PR\cap QS\) are collinear.

First solution, using projective mappings. Let \(A_3=AM\cap BC\) and \(B_3=BM\cap AC\). Let \(X\) be the other intersection point of the line \(A_1A_2\) with the circumcircle \(k\) of \(\triangle ABC\). Let \(X\prime \) be the other intersection point of the line \(B_1B_2\) with \(k\). Consider the sequence of perspectivities \[ABCX\frac{A_2}{\overline\wedge}A_3BCA_1\frac{M}{\overline\wedge}AB_3CB_1\frac{B_2}{\overline\wedge}ABCX\prime \] which has three fixed points \(A\), \(B\), \(C\), hence \(X=X\prime \). Analogously the line \(C_1C_2\) contains \(X\) and the problem is completely solved.

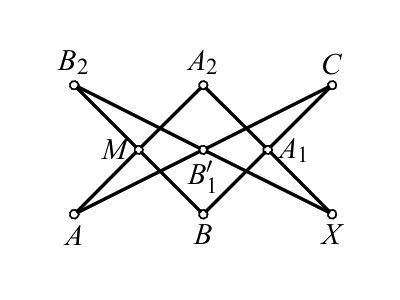
Second solution, using Pascal's theorem. Assume that the line \(A_1A_2\) intersect the circumcircle of the triangle \(ABC\) at \(A_2\) and \(X\). Let \(XB_2\cap AC=B_1\prime \). Let us apply the Pascal's theorem on the points \(A\), \(B\), \(C\), \(A_2\), \(B_2\), \(X\) according the diagram: \end{center} It follows that the points \(A_1\), \(B_1\prime \), and \(M\) are colinear. Hence \(B_1\prime \in A_1M\). According to the definition of the point \(B_1\prime \) we have \(B_1\prime \in AC\) hence \(B_1\prime =A_1M\cap AC=B_1\). The conclusion is that the points \(X\), \(B_1\), \(B_2\) are colinear. Analogously we prove that the points \(X\), \(C_1\), \(C_2\) are colinear, hence the lines \(A_1A_2\), \(B_1B_2\), \(C_1C_2\) intersect at \(X\) that belongs to the circumcircle of the triangle \(ABC\).

It is well known (from the theory of pedal triangles) that pedal triangles corresponding to the isogonally conjugated points have the common circumcircle, so called {\em pedal circle} of the points \(P\) and \(Q\). The center of that circle which is at the same time the midpoint of \(PQ\) will be denoted by \(R\). Let \(P_1\prime =PP_1\cap Q_1R\) and \(P_2\prime =PP_2\cap Q_2R\) (the points \(P_1\prime \) and \(P_2\prime \) belong to the pedal circle of the point \(P\), as point on the same diameters as \(Q_1\) and \(Q_2\) respectively). 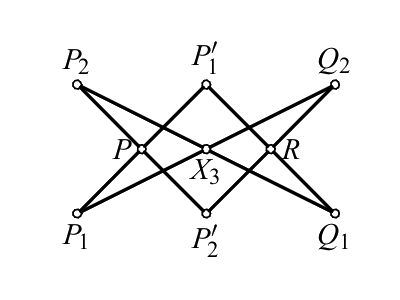Using the Pascal's theorem on the points \(Q_1\), \(P_2\), \(P_2\prime \), \(Q_2\), \(P_1\), \(P_1\prime \) in the order shown by the diagram we get that the points \(P\), \(R\), \(X_1\) are colinear or \(X_1\in PQ\). Analogously the points \(X_2\), \(X_3\) belong to the line \(PQ\).

Let us recall the statement according to which the circle \(l\) is invariant under the inversion with respect to the circle \(k\) if and only if \(l=k\) or \(l\perp k\).

Since the point \(M\) belongs to the polar of the point \(A\) with respect to \(k\) we have \(\angle MA^*A=90^\circ\) where \(A^*=\psi_l(A)\). Therefore \(A^*\in l\) where \(l\) is the circle with the radius \(AM\). Analogously \(M^*\in l\). However from \(A\in l\) we get \(A^*\in l^*\); \(A^*\in l\) yields \(A\in l^*\) (the inversion is inverse to itself) hence \(\psi_l(A^*)=A\)). Similarly we get \(M\in l^*\) and \(M^*\in l^*\). Notice that the circles \(l\) and \(l^*\) have the four common points \(A\), \(A^*\), \(M\), \(M^*\), which is exactly two too much. Hence \(l=l^*\) and according to the statement mentioned at the beginning we conclude \(l=k\) or \(l\perp k\). The case \(l=k\) can be easily eliminated, because the circle \(l\) has the diameter \(AM\), and \(AM\) can't be the diameter of \(k\) because \(A\) and \(M\) are conjugated to each other.

Thus \(l\perp k\), q.e.d.

Let \(J=KL\cap MN\), \(R=l\cap MN\), \(X_\infty=l\cap AM\). Since \(MN\) is the polar of \(A\) from \(J\in MN\) we get \(\mathcal H(K,L;J,A)\). From \(KLJA\frac{M}{\overline\wedge}PQRX_\infty\) we also have \(\mathcal H(P,Q;R,X_\infty)\). This implies that \(R\) is the midpoint of \(PQ\).

Let \(Q\) be the intersection point of the lines \(AP\) and \(BC\). Let \(Q\prime \) be the point of \(BC\) such that the ray \(AQ\prime \) is isogonal to the ray \(AQ\) in the triangle \(ABC\). This exactly means that \(\angle Q\prime AC=\angle BAQ\) i \(\angle BAQ\prime =\angle QAC\).

For an arbitrary point \(X\) of the segment \(BC\), the sine theorem applied to triangles \(BAX\) and \(XAC\) yields \[\frac{BX}{XC}=\frac{BX}{AX} \frac{AX}{XC}= \frac{\sin\angle BAX}{\sin\angle ABX} \frac{\sin\angle ACX}{\sin\angle XAC}= \frac{\sin\angle ACX}{\sin\angle ABX} \frac{\sin\angle BAX}{\sin\angle XAC}=\frac{AB}{AC} \frac{\sin\angle BAX}{\sin\angle XAC}.\] Applying this to \(X=Q\) and \(X=Q\prime \) and multiplying together afterwards we get \[\frac{BQ}{QC} \frac{BQ\prime }{Q\prime C}=\frac{AB}{AC} \frac{\sin\angle BAQ}{\sin\angle QAC} \frac{AB}{AC} \frac{\sin\angle BAQ\prime }{\sin\angle Q\prime AC} = \frac{AB^2}{AC^2}. \quad\quad\quad\quad\quad (1)\] Hence if we prove \(BQ/QC=AB^2/AC^2\) we would immediately have \(BQ\prime /Q\prime C=1\), making \(Q\prime \) the midpoint of \(BC\). Then the line \(AQ\) is isogonaly conjugated to the median, implying the required statement.

Since \(P\) belongs to the polars of \(B\) and \(C\), then the points \(B\) and \(C\) belong to the polar of the point \(P\), and we conclude that the polar of \(P\) is precisely \(BC\). Consider the intersection \(D\) of the line \(BC\) with the tangent to the circumcircle at \(A\). Since the point \(D\) belongs to the polars of \(A\) and \(P\), \(AP\) has to be the polar of \(D\). Hence \(\mathcal H(B,C;D,Q)\). Let us now calculate the ratio \(BD/DC\). Since the triangles \(ABD\) and \(CAD\) are similar we have \(BD/AD=AD/CD=AB/AC\). This implies \(BD/CD=(BD/AD) (AD/CD)=AB^2/AC^2\). The relation \(\mathcal H(B,C;D,Q)\) implies \(BQ/QC=BD/DC=AB^2/AC^2\), which proves the statement.

The statement follows from the Brianchon's theorem applied to \(APBMCN\).

Applying the Brianchon's theorem to the hexagon \(AMBCPD\) we get that the line \(MP\) contains the intersection of \(AB\) and \(CD\). Analogously, applying the Brianchon's theorem to \(ABNCDQ\) we get that \(NQ\) contains the same point.

The Brokard's theorem claims that the polar of \(F=AD\cap BC\) is the line \(f=EO\). Since the polar of the point on the circle is equal to the tangent at that point we know that \(K=a\cap d\), where \(a\) and \(d\) are polars of the points \(A\) and \(D\). Thus \(k=AD\). Since \(F\in AD=k\), we have \(K\in f\) as well. Analogously we can prove that \(L\in f\), hence the points \(E\), \(O\), \(K\), \(L\) all belong to \(f\).

Let \(G=AD\cap BC\). Let \(k\) be the circumcircle of \(ABCD\). Denote by \(k_1\) and \(k_2\) respectively the circumcircles of \(\triangle ADF\) and \(\triangle BCF\). Notice that \(AD\) is the radical axis of the circles \(k\) and \(k_1\); \(BC\) the radical axis of \(k\) and \(k_2\); and \(FH\) the radical axis of \(k_1\) and \(k_2\). According to the famous theorem these three radical axes intersect at one point \(G\). In other words we have shown that the points \(F\), \(G\), \(H\) are colinear.

Without loss of generality assume that \(F\) is between \(G\) and \(H\) (alternatively, we could use the oriented angles). Using the inscribed quadrilaterals \(ADFH\) and \(BCFH\), we get \(\angle DHF= \angle DAF=\angle DAC\) and \(\angle FHC=\angle FBC=\angle DBC\), hence \(\angle DHC=\angle DHF+\angle FHC=\angle DAC +\angle DBC=2\angle DAC=\angle DOC\). Thus the points \(D\), \(C\), \(H\), and \(O\) lie on a circle. Similarly we prove that the points \(A\), \(B\), \(H\), \(O\) lie on a circle.

Denote by \(k_3\) and \(k_4\) respectively the circles circumscribed about the quadrilaterals \(ABHO\) and \(DCHO\). Notice that the line \(AB\) is the radical axis of the circles \(k\) and \(k_3\). Simlarly \(CD\) and \(OH\), respectively, are those of the pairs of circles \((k,k_2)\) and \((k_3,k_4)\). Thus these lines have to intersect at one point, and that has to be \(E\). This proves that the points \(O\), \(H\), and \(E\) are colinear.

According to the Brocard's theorem we have \(FH\bot OE\), which according to \(FH=GH\) and \(OE=HE\) in turn implies that \(GH\bot HE\), q.e.d.