| 1. | Cross ratio. Harmonic conjugates. Perspectivity. Projectivity |
| 2. | Desargue's theorem |
| 3. | Theorems of Pappus and Pascal |
| 4. | Pole. Polar. Theorems of Brianchon and Brokard |
| 5. | Problems |
Pole. Polar. Theorems of Brianchon and Brokard
Definition
Given a circle \(k(O,r)\), let \(A^*\)
be the image of the point \(A\neq O\)
under the inversion with respect to \(k\).
The line \(a\) passing through
\(A^*\) and perpendicular to \(OA\)
is called the polar of \(A\)
with respect to \(k\).
Conversely \(A\) is called the pole of \(a\)
with respect to \(k\).
Theorem 6
Given a circle \(k(O,r)\), let
and \(a\) and \(b\) be the polars of
\(A\) and \(B\) with respect to \(k\).
The \(A\in b\) if and only if \(B\in a\).
Definition
Points \(A\) and \(B\) are called conjugated with respect
to the circle
\(k\) if one of them lies on a polar of the other.
Theorem 7
If the line determined by two conjugated points \(A\) and
\(B\) intersects \(k(O,r)\) at \(C\) and \(D\),
then \(\mathcal H(A,B;C,D)\). Conversely if \(\mathcal H(A,B;C,D)\),
where \(C,D\in k\) then \(A\) and \(B\) are conjugated
with respect to \(k\).
Theorem 8 (Brianchon)
Assume that the hexagon
\(A_1A_2A_3A_4A_5A_6\) is circumscribed about the circle \(k\).
The lines \(A_1A_4\), \(A_2A_5\), and \(A_3A_6\)
intersect at a point.
From the previous proof we see that the Brianchon\(\prime\)s theorem is obtained from the Pascal\(\prime\)s by replacing all the points with their polars and all lines by theirs poles.
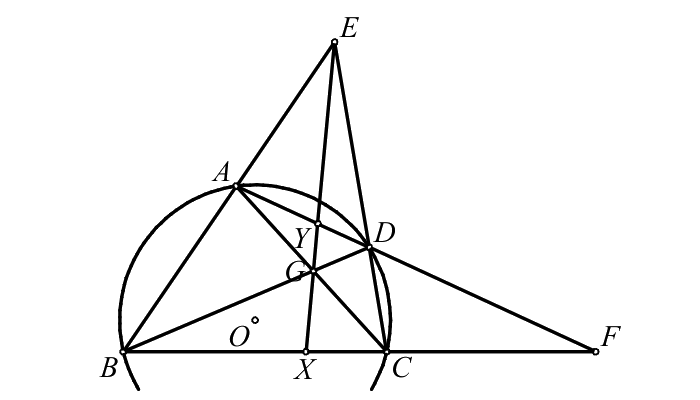
Theorem 9 (Brokard)
The quadrilateral \(ABCD\) is inscribed in the circle
\(k\) with center \(O\). Let \(E=AB\cap CD\),
\(F=AD\cap BC\), \(G=AC\cap BD\).
Then \(O\) is the orthocenter of the triangle
\(EFG\).