1.	Cross ratio. Harmonic conjugates. Perspectivity. Projectivity
2.	Desargue's theorem
3.	Theorems of Pappus and Pascal
4.	Pole. Polar. Theorems of Brianchon and Brokard
5.	Problems

Cross ratio. Harmonic conjugates. Perspectivity. Projectivity

Definition Let \(A\), \(B\), \(C\), and \(D\) be colinear points. The cross ratio of the pairs of points \((A,B)\) and \((C,D)\) is \[ \mathcal{R}(A,B;C,D) = \frac{\overrightarrow{AC}} {\overrightarrow{CB}}:\frac{\overrightarrow{AD}} {\overrightarrow{DB}}. \quad\quad\quad\quad\quad (1) \]

Let \(a\), \(b\), \(c\), \(d\) be four concurrent lines. For the given lines \(p_1\) and \(p_2\) let us denote \(A_i=a\cap p_i\), \(B_i=b\cap p_i\), \(C_i=c\cap p_i\), \(D_i=d\cap p_i\), for \(i=1\), \(2\). Then \[\mathcal R(A_1,B_1;C_1,D_1)= \mathcal R(A_2,B_2;C_2,D_2).\quad\quad\quad\quad\quad (2)\]

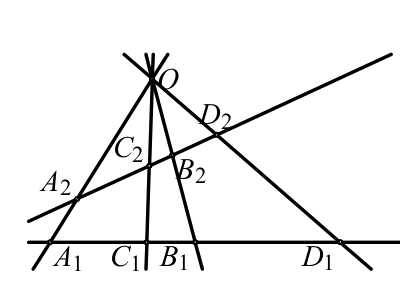
Thus it is meaningful to define the cross ratio of the pairs of concurrent lines as \[ \mathcal R(a,b;c,d)=\mathcal R(A_1,B_1;C_1,D_1). \quad\quad\quad\quad\quad (3)\]

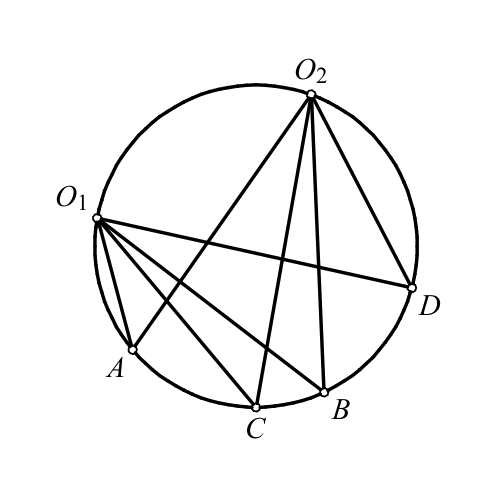
Assume that points \(O_1\), \(O_2\), \(A\), \(B\), \(C\), \(D\) belong to a circle. Then \[ \mathcal R(O_1A,O_1B;O_1C,O_1D) = \mathcal R(O_2A,O_2B;O_2C,O_2D).\quad\quad\quad\quad\quad (4)\] Hence it is meaningful to define the cross-ratio for cocyclic points as \[ \mathcal R(A,B;C,D) =\mathcal R(O_1A,O_1B;O_1C,O_1D).\quad\quad\quad\quad\quad (5)\] Assume that the points \(A\), \(B\), \(C\), \(D\) are colinear or cocyclic. Let an inversion with center \(O\) maps \(A\), \(B\), \(C\), \(D\) into \(A^*\), \(B^*\), \(C^*\), \(D^*\). Then \[\mathcal R(A,B;C,D)=\mathcal R(A^*,B^*;C^*,D^*). \quad\quad\quad\quad\quad (6)\]

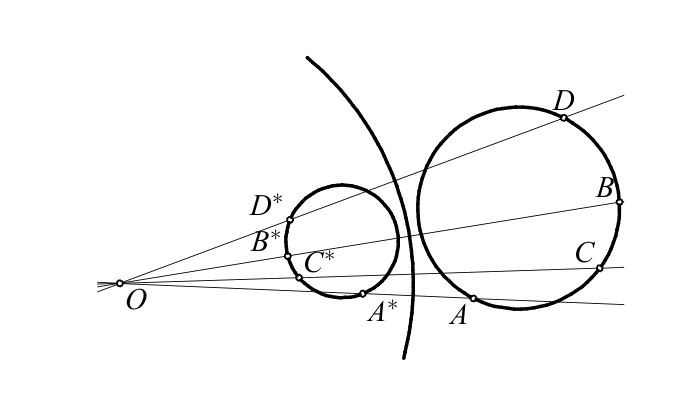
Definition Assume that \(A\), \(B\), \(C\), and \(D\) are cocyclic or colinear points. Pairs of points \((A,B)\) and \((C,D)\) are harmonic conjugates if \(\mathcal R(A,B;C,D)=-1\). We also write \(\mathcal H(A,B;C,D)\) when we want to say that \((A,B)\) and \((C,D)\) are harmonic conjugates to each other.

Definition Let each of \(l_1\) and \(l_2\) be either line or circle. Perspectivity with respect to the point \(S\) (denote as \(\frac{S}{\overline\wedge}\)), is the mapping of \(l_1\rightarrow l_2\), such that

(i) If either \(l_1\) or \(l_2\) is a circle than it contains \(S\);

(ii) every point \(A_1\in l_1\) is mapped to the point \(A_2=OA_1\cap l_2\).

According to the previous statements perspectivity preserves the cross ratio and hence the harmonic conjugates.

Definition Let each of \(l_1\) and \(l_2\) be either line or circle. Projectivity is any mapping from \(l_1\) to \(l_2\) that can be represented as a finite composition of perspectivities.

Theorem 1 Assume that the points \(A\), \(B\), \(C\), \(D_1\), and \(D_2\) are either colinear or cocyclic. If the equation \(\mathcal R(A,B;C,D_1)= \mathcal R(A,B;C,D_2)\) is satisfied, then \(D_1=D_2\). In other words, a projectivity with three fixed points is the identity.

Theorem 2 If the points \(A\), \(B\), \(C\), \(D\) are mutually discjoint and \(\mathcal R(A,B;C,D)=\mathcal R(B,A;C,D)\) then \(\mathcal H(A,B;C,D)\).