8. Pointers, Linked Lists, Stacks, and Sequences: Practice Problems
The user input consists of a positive integer \(n\) followed by \(n\) words \(w[0]\), \(w[1]\), \(\dots\), \(w[n-1]\) of type std::string. After these \(n\) words, the user inputs two integers \(k\) and \(l\) such that \(0\leq k < l \leq n\). Create the program that reads the input from std::cin and prints the words \(w[k]\), \(w[k+1]\), \(\dots\), \(w[l-1]\).
Create the function divisibleByP whose arguments are the pointer to the first term of the sequence, the length of the sequence, and the integer \(p\). The output function divisibleByP should create the new sequence \(y\) with the following property: \(y[0]\) should be the total number of terms of the sequence \(x\) that are divisible by \(p\). The elements \(y[1]\), \(y[2]\), \(\dots\) should be the actual terms of \(x\) that are divisible by \(p\).
Create the program that uses the function divisibleByP. The user input consists of a positive integer \(n\) followed by \(n\) integers \(x[0]\), \(x[1]\), \(\dots\), \(x[n-1]\). The user then inputs the integer \(p\). Use the function divisibleByP to create the sequence of those terms that are divisible by \(p\) and print them on the standard output.
Create a function that starts from a sequence \( x \) of integers of length \( n \) and modifies it so that every occurrence of the number \( 5 \) is deleted, and every occurrence of number 0 is replaced with three numbers \( 1 \). For example if \( n=8 \), and \( x=(1,8,0,3,5,7,0,8) \), then the resulting sequence is \[ x=(1,8,1,1,1,3,7,1,1,1,8).\]
The user enters the integers though the standard input. The input -9 is the end, and unless it is the first integer, it is not to be considered the part of the input. Create a linked list from the numbers that the user has entered. The user enters another integer. If this integer is in the list, delete its last occurrence from the list and print the remaining list. If it is not in the list, print the original list.
The box factory is making boxes. It labels all of its boxes with distinct integers. Each box has two parts: top and bottom. The bottom is labeled with a positive integer and the top is labeled with the negative integer in such a way that for each box the sum of the two labels is zero.
Both top and bottom parts are heavy and a team of employees is necessary to lift each of them. The manager wants to put some of the boxes inside other boxes and send them away. So if the manager wants to put the box \( 10 \) inside the box \( 30 \), then he needs to clearly indicate to the team that they need to perform the following four steps:
- 1. Bring the bottom of the box 30.
- 2. Bring the bottom of the box 10 and put it inside the box 30.
- 3. Bring the top of the box 10 (which has the label -10) and close it.
- 4. Bring the top of the box 30 (which has the label -30) and close it.
This results in the box \( 10 \) being placed inside the box \( 30 \). The box \( 10 \) becomes invisible and only one box needs to get sent for shipping.
The manager communicates with the team by sending them a sequence of integers. In this case, when the box 10 has to be placed inside the box 30, the sequence is \( 30 \), \( 10 \), \( -10 \), \( -30 \).
Create the program that calculates the total number of shipments that the team will make. The input starts with an even integer \( N \) followed by the sequence \( x_0 \), \( x_1 \), \( \dots \), \( x_{N-1} \) of distinct integers different from \( 0 \) that represent the instructions that the manager sends to the team. If the instructions result in some boxes being improperly closed, print a message that the sequence is bad.
Example 1:
Input: 12 30 10 -10 -30 60 7 -7 50 8 -8 -50 -60 Output: 2
Explanation: The box \( 10 \) gets into the box \( 30 \). The box \( 7 \) is placed in the box \( 60 \). After the box \( 7 \) is closed, the box \( 50 \) is placed inside the box \( 60 \), and the box \( 8 \) inside the box \( 50 \). In total, there are only \( 2 \) boxes that are shipped: \( 30 \) and \( 60 \).
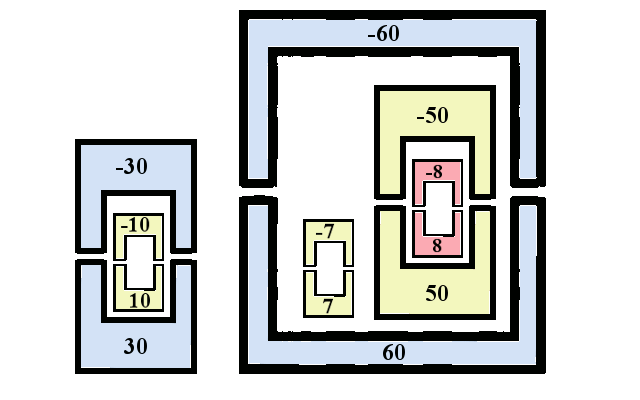
Example 2:
Input: 6 7 8 9 -8 -9 -7 Output: Bad sequence
Explanation: The top part of the box \( 8 \) is brought before the top part of the box \( 9 \). This would leave the box \( 9 \) open and inside of the box \( 8 \).