Case 2.2.1: Calculation of \(P_{2.2.1^{\circ}}(k)\)
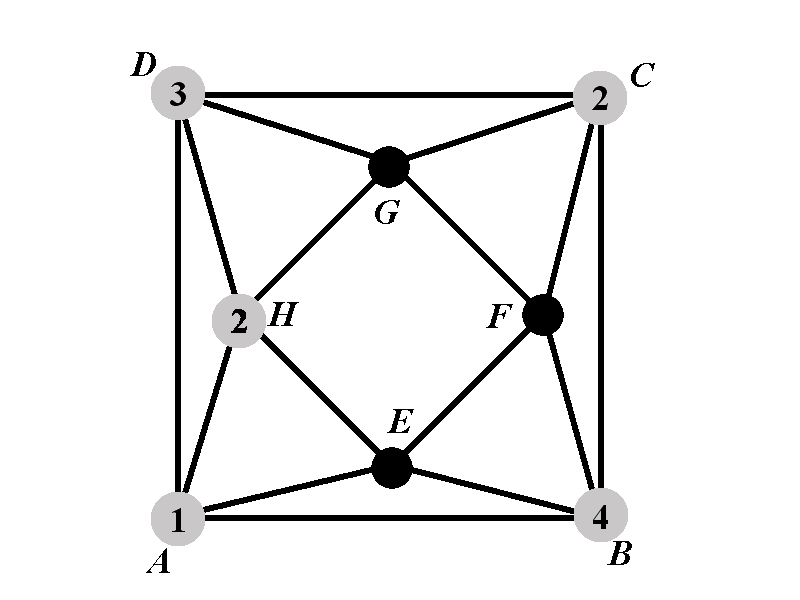
Observe that the vertex \(G\) cannot have a color \(2\) or \(3\). We will consider 3 sub-cases. Sub-case 2.2.1.1 is in which the vertex \(G\) has color \(1\). Sub-case 2.2.1.2 is the sub-case in which \(G\) has color \(4\), and sub-case 2.2.1.3 is the sub-case in which \(G\) has a color outside of the set \(\{1,2,3,4\}\).
Let us introduce the following polynomials that correspond to sub-cases 2.2.1.1, 2.2.1.2, and 2.2.1.3.
- Denote by \(P_{2.2.1.1^{\circ}}(k)\) the number of proper colorings of \(\Gamma\) in \(k\) colors such that the vertices \(A\), \(B\), \(C\), \(D\), \(G\), and \(H\) have the colors \(1\), \(4\), \(2\), \(3\), \(1\), and \(2\), respectively.
- Denote by \(P_{2.2.1.2^{\circ}}(k)\) the number of proper colorings of \(\Gamma\) in \(k\) colors such that the vertices \(A\), \(B\), \(C\), \(D\), \(G\), and \(H\) have the colors \(1\), \(4\), \(2\), \(3\), \(4\), and \(2\), respectively.
- Denote by \(P_{2.2.1.3^{\circ}}(k)\) the number of proper colorings of \(\Gamma\) in \(k\) colors such that the vertices \(A\), \(B\), \(C\), \(D\), \(G\), and \(H\) have the colors \(1\), \(4\), \(2\), \(3\), \(5\), and \(2\), respectively.
The polynomial \(P_{2.2.1^{\circ}}(k)\) can be expressed in terms of these newly introduced polynomials as \[P_{2.2.1^{\circ}}(k)=P_{2.2.1.1^{\circ}}(k)+P_{2.2.1.2^{\circ}}(k)+(k-4)P_{2.2.1.3^{\circ}}(k).\] The last polynomial is multiplied by \((k-4)\) because if the vertex \(G\) does not have any of the colors from \(\{1,2,3,4\}\), then the number of available colors for \(G\) is \(k-4\).
- Calculation of \(P_{2.2.1.1^{\circ}}(k)\) shows that \(P_{2.2.1.1^{\circ}}=(k-3)(k-4)\).
- Calculation of \(P_{2.2.1.2^{\circ}}(k)\) shows that \(P_{2.2.1.2^{\circ}}(k)=(k-3)^2\).
- Calculation of \(P_{2.2.1.3^{\circ}}(k)\) shows that \(P_{2.2.1.3^{\circ}}(k)= k-3+(k-4)^2\).
Therefore the polynomial \(P_{2.2.1^{\circ}}(k)\) satisfies \begin{eqnarray*} P_{2.2.1^{\circ}}(k)&=&P_{2.2.1.1^{\circ}}(k)+P_{2.2.1.2^{\circ}}(k)+(k-4)P_{2.2.1.3^{\circ}}(k)\newline &=&(k-3)(k-4)+(k-3)^2+(k-4)\left( k-3+(k-4)^2\right)\newline &=&k^3-9k^2+28k-31. \end{eqnarray*}