Case 2.2.1.3: Calculation of \(P_{2.2.1.3^{\circ}}(k)\)
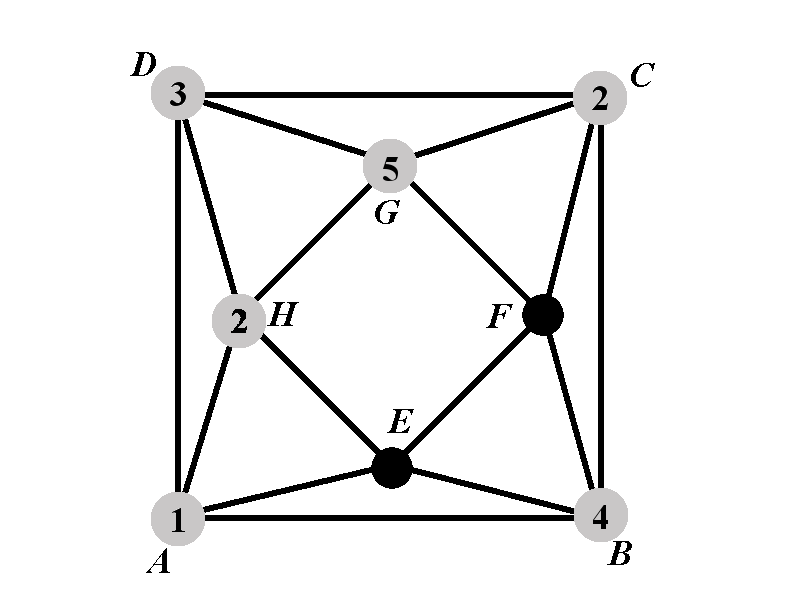
The vertex \(F\) cannot have colors \(2\), \(4\), and \(5\). We will consider two sub-cases. In the sub-case 2.2.1.3.1 we count all the proper colorings of \(\Gamma\) in which the vertex \(F\) has color \(1\). In the sub-case 2.2.1.3.2 we count all the proper colorings of \(\Gamma\) in which the vertex \(F\) does not have a color from \(\{1,2,4,5\}\). In the sub-case 2.2.1.3.2 there are \((k-4)\) possible colors that can be assigned to \(F\).
Let \(P_{2.2.1.3.1^{\circ}}(k)\) be the number of proper colorings of \(\Gamma\) in which the vertices \(A\), \(B\), \(C\), \(D\), \(F\), \(G\), and \(H\) have the colors \(1\), \(4\), \(2\), \(3\), \(1\), \(5\), and \(2\), respectively. Let \(P_{2.2.1.3.2^{\circ}}(k)\) be the number of proper colorings of \(\Gamma\) in which the vertices \(A\), \(B\), \(C\), \(D\), \(F\), \(G\), and \(H\) have the colors \(1\), \(4\), \(2\), \(3\), \(3\), \(5\), and \(2\), respectively. The following identity holds
\[P_{2.2.1.3^{\circ}}(k)=P_{2.2.1.3.1^{\circ}}(k)+(k-4)P_{2.2.1.3.2^{\circ}}(k).\]Case 2.2.1.3.1: Calculation of \(P_{2.2.1.3.1^{\circ}}(k)\)
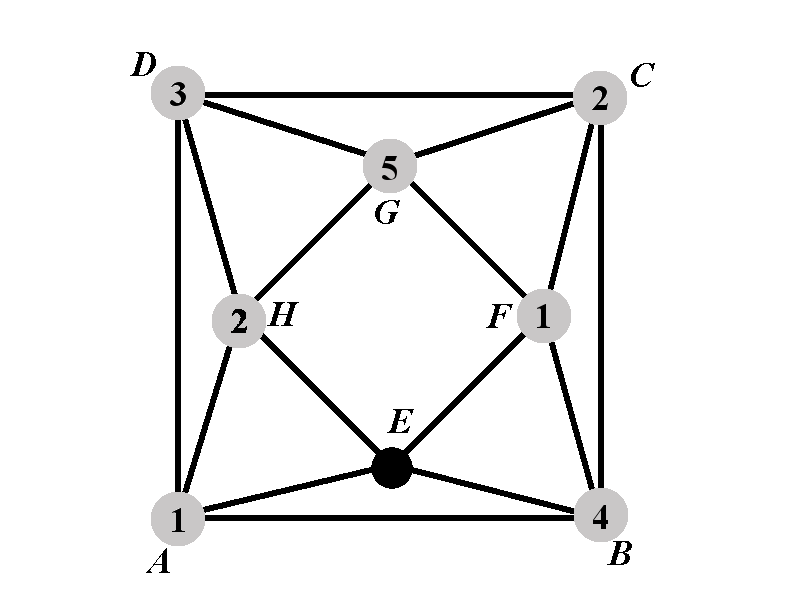
It remains to count the number of ways in which the vertex \(E\) can be colored. The vertex \(E\) must not have any of the colors \(1\), \(2\), and \(4\). That leaves \(k-3\) available colors for the vertex \(E\). Therefore \[P_{2.2.1.3.1^{\circ}}(k)=k-3.\]
Case 2.2.1.3.2: Calculation of \(P_{2.2.1.3.2^{\circ}}(k)\)
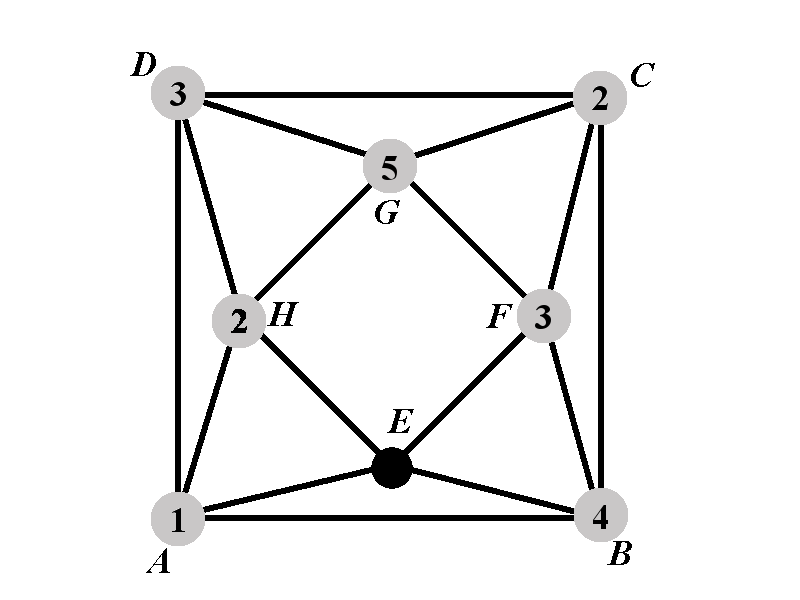
The vertex \(E\) must not have any of the colors \(1\), \(2\), \(3\), and \(4\). The number of available colors for \(E\) is \(k-4\). Therefore \[P_{2.2.1.3.2^{\circ}}(k)=k-4.\]
Thus we have \begin{eqnarray*}P_{2.2.1.3^{\circ}}(k)&=&P_{2.2.1.3.1^{\circ}}(k)+(k-4)P_{2.2.1.3.2^{\circ}}(k)\newline &=&k-3+(k-4)^2. \end{eqnarray*}