Back to: Chromatic Polynomial Case \(2.2.1^{\circ}\)
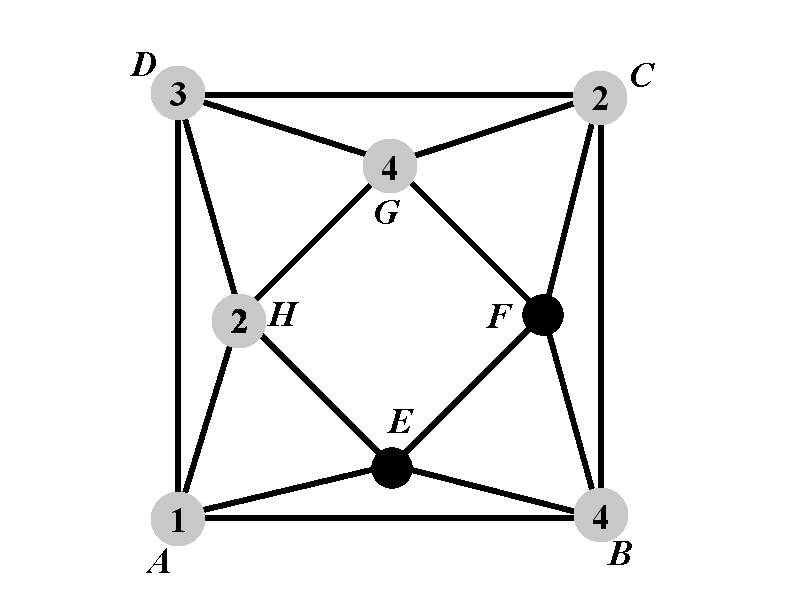
Case 2.2.1.2: Calculation of \(P_{2.2.1.2^{\circ}}(k)\)

Observe that the vertex \(E\) cannot have any of the colors \(1\), \(2\), and \(4\). There are \(k-3\) ways to assign a color to \(E\). The color assigned to \(F\) will not be \(2\) nor \(4\). Thus, each assignment of the color to the vertex \(E\) leaves exactly \(k-3\) possible colors for \(F\). The vertex \(F\) cannot have color \(2\), nor color \(4\), nor the color assigned to \(E\). Therefore \[P_{2.2.1.2^{\circ}}(k)=(k-3)^2.\]