Back to: Chromatic Polynomial Case \(2.2.1^{\circ}\)
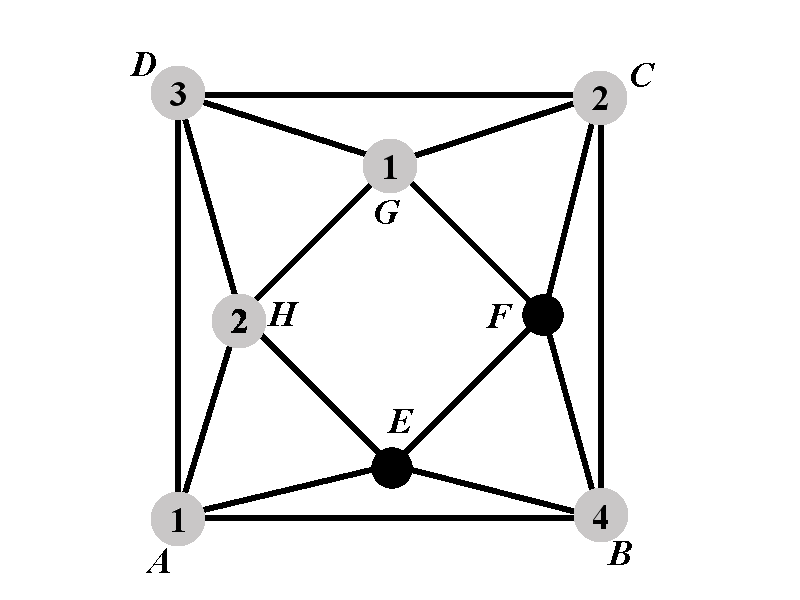
Case 2.2.1.1: Calculation of \(P_{2.2.1.1^{\circ}}(k)\)

We need to determine the number of ways to assign colors to the vertices \(E\) and \(F\). Notice that none of the vertices \(E\) and \(F\) can have any of the colors \(1\), \(2\), and \(4\). Also, the vertices \(E\) and \(F\) must have distinct colors. It remains to notice that there are no other restrictions on the colors of \(E\) and \(F\). Therefore the number of ways to assign a color to \(E\) is \(k-3\). For each assignment of color to \(E\) there are \(n-4\) possible colors to assign to \(F\). Therefore \[P_{2.2.1.1^{\circ}}=(k-3)(k-4).\]