Case 2.2: Calculation of \(P_{2.2^{\circ}}(k)\)
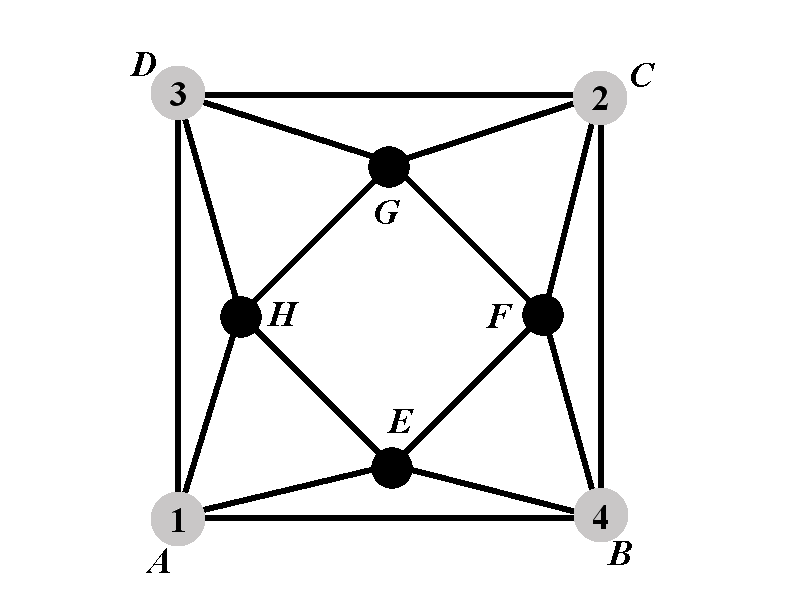
We will now consider two sub-cases: Sub-case \(2.2.1^{\circ}\) is when the vertex \(H\) is of one of the colors \(\{2,4\}\); and sub-case \(2.2.2^{\circ}\) is when the vertex \(H\) does not have one of the colors from \(\{2,4\}\).
The number of proper colorings in which \(H\) has color \(2\) is equal to the number of proper colorings in which \(H\) is of color \(4\). Therefore we will cacluate only the number of proper colorings in which \(H\) has color \(2\). We will denote by \(P_{2.2.1^{\circ}}(k)\) the number of proper colorings in which \(H\) has color \(2\), and as specified earlier \(A\), \(B\), \(C\), and \(D\) have colors \(1\), \(4\), \(2\), and \(3\) respectively.
Notice that \(H\) cannot have color \(1\) nor color \(3\). Therefore, if \(H\) has a color outside of the set \(\{2,4\}\), then \(H\) must not have any of the colors from \(\{1,2,3,4\}\). The number of colorings in the case \(2.2.2^{\circ}\) is \((k-4)\cdot P_{2.2.2^{\circ}}(k)\) where \(P_{2.2.2^{\circ}}(k)\) is the number of proper colorings of \(\Gamma\) in which \(A\), \(B\), \(C\), \(D\), and \(H\) have colors \(1\), \(4\), \(2\), \(3\), and \(5\) respectively.
The number \(P_{2.2^{\circ}}(k)\) satisfies \[P_{2.2^{\circ}}(k)=2\cdot P_{2.2.1^{\circ}}(k)+(k-4)\cdot P_{2.2.2^{\circ}}(k).\]
- Calculation of \(P_{2.2.1^{\circ}}(k)\) shows that \(P_{2.2.1^{\circ}}(k)=k^3-9k^2+28k-31\).
- Calculation of \(P_{2.2.2^{\circ}}(k)\) shows that \(P_{2.2.2^{\circ}}(k)=k^3-10k^2+36k-47\).
Therefore the polynomial \(P_{2.2^{\circ}}(k)\) satisfies \begin{eqnarray*}P_{2.2^{\circ}}(k)&=&2\cdot P_{2.2.1^{\circ}}(k)+(k-4)\cdot P_{2.2.2^{\circ}}(k)\newline &=&2\left(k^3-9k^2+28k-31\right)+(k-4)\left(k^3-10k^2+36k-47\right)\newline &=&2k^3-18k^2+56k-62+(k-3)\left(k^3-10k^2+36k-47\right)-\left(k^3-10k^2+36k-47\right)\newline &=&k^3-8k^2+20k-15+(k-3)\left(k^3-10k^2+36k-47\right)\newline &=&k^3-3k^2-5k^2+15k+5k-15+(k-3)\left(k^3-10k^2+36k-47\right)\newline &=&(k-3)\left(k^2-5k+5\right)+(k-3)\left(k^3-10k^2+36k-47\right)\newline \ &=&(k-3)\left(k^3-9k^2+31k-42\right). \end{eqnarray*}