Chromatic polynomial
Assume that \(G=(V,E)\) is a simple non-directed graph. For positive integer \(k\) we denote by \(\chi_G(k)\) the number of ways in which the vertices of \(G\) can be colored with \(k\) colors such that no two vertices share the same color.
It can be proved by induction that \(\chi_G(k)\) is a polynomial in \(k\) for every graph \(G\). We will skip this proof. After seeing few examples this fact will not be surprising.
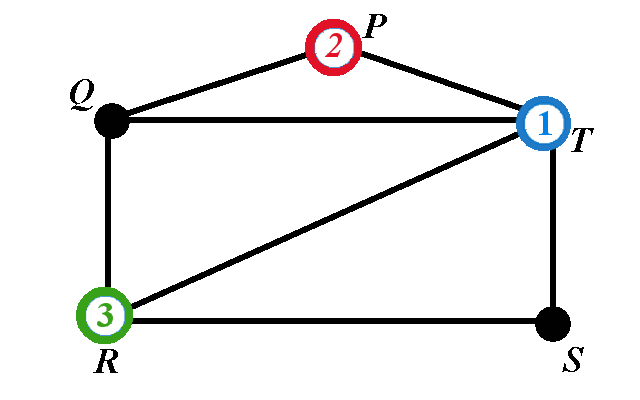
Determine the chromatic polynomial of the graph below
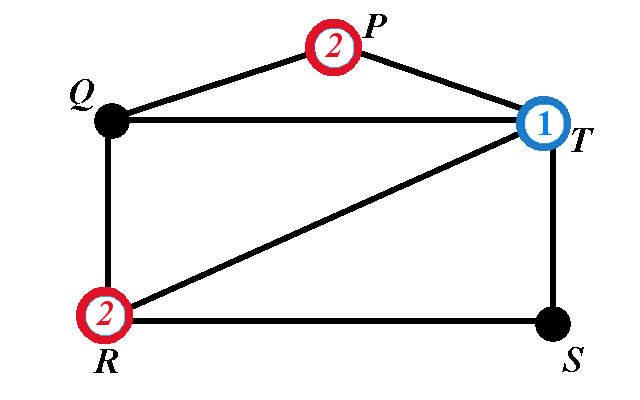
If the chromatic polynomial of a graph is \(\chi_G(x)=x(x-1)(x-2)\left(x^2-5x+6\right)\), determine the chromatic number of the graph.
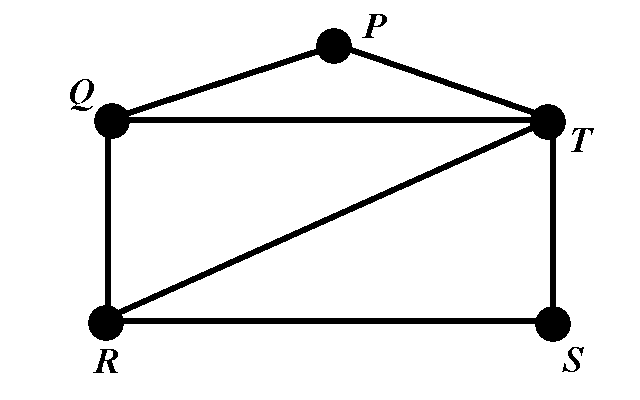
Determine the chromatic polynomial of the graph below
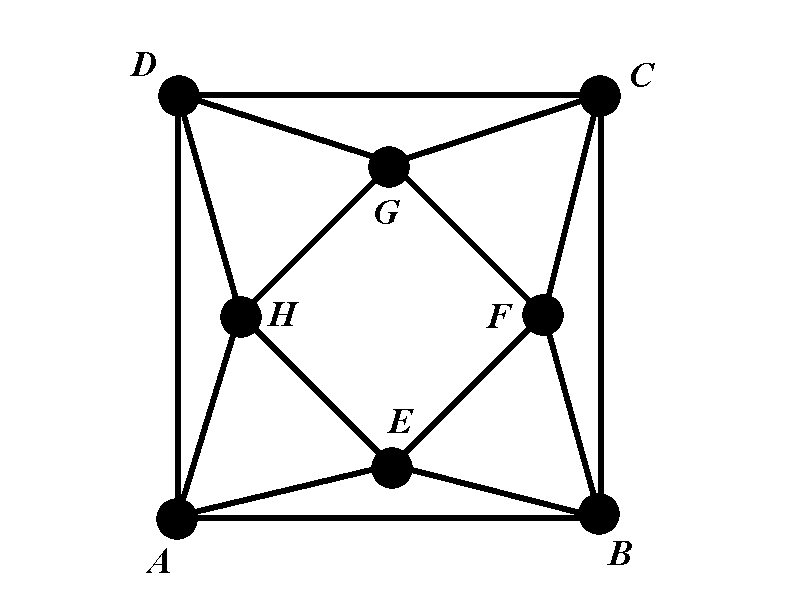
There are many ways to solve this problem. In each of them the calculation will be long and tedious and we need to consider numerous cases.
Let us denote by \(\Gamma\) the graph above. For given positive integer \(k\) the value of the chromatic polynomial \(\chi_{\Gamma}(k)\) is the number of ways in which the vertices of \(\Gamma\) can be colored with colors \(\{1,2,\dots, k\}\) so that no two adjacent vertices are of the same color.
We will consider two major cases: \(1^{\circ}\) vertices \(A\) and \(C\) are of the same color and \(2^{\circ}\) vertices \(A\) and \(C\) are of different colors. We formalize this division into two cases by defining the two polynomials \(\chi_{1^{\circ}}(k)\) and \(\chi_{2^{\circ}}(k)\) in the following way.
- \(1^{\circ}\) Denote by \(\chi_{1^{\circ}}(k)\) the number of proper colorings of \(\Gamma\) in which \(A\) and \(C\) have the same color.
- \(2^{\circ}\). Denote by \(\chi_{2^{\circ}}(k)\) the number of proper colorings of \(\Gamma\) in which \(A\) and \(C\) have different colors.
The chromatic polynomial \(\chi_{\Gamma}\) satisfies \[\chi_{\Gamma}(k)=\chi_{1^{\circ}}(k)+\chi_{2^{\circ}}(k).\]
Case 1: Calculation of \(\chi_{1^{\circ}}(k)\)
There are \(k\) ways to choose the color for the vertices \(A\) and \(C\). Thus \(\chi_{1^{\circ}}(k)\) is obtained when the number \(k\) is multiplied by the number of proper colorings in which the vertices \(A\) and \(C\) have the color \(1\). Assume thus that the vertices \(A\) and \(C\) are of color \(1\). The colors of the vertices \(D\), \(G\), and \(H\) must be different from each other and different from \(1\). The number of ways to choose a color for \(D\) is \(k-1\). For each of the choices of the color for \(D\) there are \(k-2\) available colors for \(H\). For each of the choices for colors for \(D\) and \(H\) there are \(k-3\) available colors for the vertex \(G\). Let us denote by \(P_{1^{\circ}}(k)\) the number of proper colorings of \(\Gamma\) in which the vertices \(A\), \(C\), \(D\), \(G\), and \(H\) have the colors \(1\), \(1\), \(2\), \(4\), and \(3\), respectively. Then we have the following relation between \(\chi_{1^{\circ}}(k)\) and \(P_{1^{\circ}}(k)\) \[\chi_1^{\circ}=k(k-1)(k-2)(k-3)P_{1^{\circ}}(k).\]
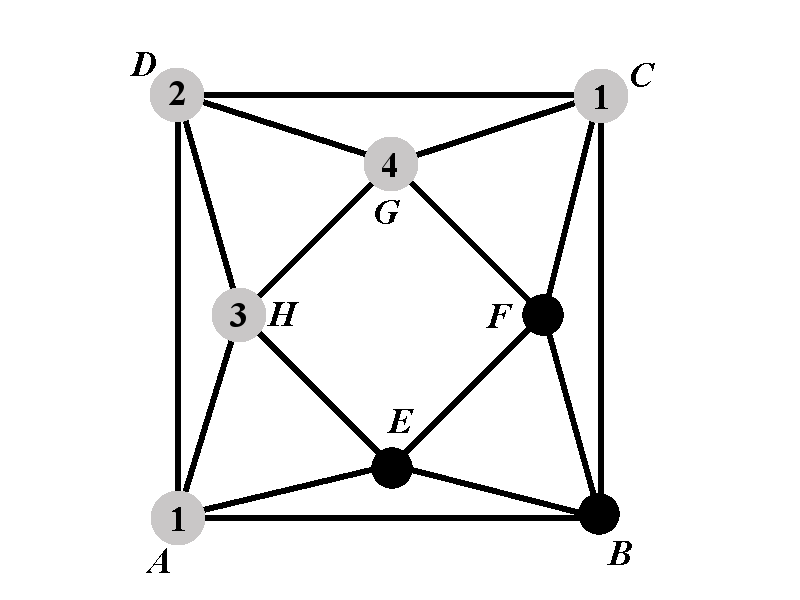
The vertex \(B\) cannot have the color \(1\). We will distinguish two sub-cases. Sub-case 1.1 is when the vertex \(B\) has one of the colors from \(\{3,4\}\). Sub-case 1.2 is when the vertex \(B\) has a color that is not in the set \(\{1,3,4\}\).
The consideration of the sub-case 1.1 is simplified one we notice that the number of proper colorings when \(B\) is of color \(3\) is equal to the number of proper colorings when \(B\) is of color \(4\). Let us denote by \(P_{1.1^{\circ}}(k)\) the number of proper colorings of \(\Gamma\) in which the vertices \(A\), \(B\), \(C\), \(D\), \(G\), and \(H\) have the colors \(1\), \(3\), \(1\), \(2\), \(4\), and \(3\), respectively. The number of colorings in sub-case 1.1 is \(2\cdot P_{1.1^{\circ}}(k)\).
We can do a similar simplification in the sub-case 1.2. There are \(k-3\) choices for the color of the vertex \(B\) - the colors that are not available are \(1\), \(3\), and \(4\). Let us denote by \(P_{1.2^{\circ}}(k)\) the number of proper colorings of \(\Gamma\) in which \(B\) has the color \(2\). In other words \(P_{1.2^{\circ}}(k)\) is the number of colorings in which the vertices \(A\), \(B\), \(C\), \(D\), \(G\), and \(H\) have the colors \(1\), \(2\), \(1\), \(2\), \(4\), and \(3\), respectively. Then the number of colorings in sub-case 1.2 is \((k-3)\cdot P_{1.2^{\circ}}(k)\).
The number \(P_{1^{\circ}}(k)\) satisfies \[ P_{1^{\circ}}(k)=2P_{1.1^{\circ}}(k)+(k-3)P_{1.2^{\circ}}(k).\]
- Calculation of \(P_{1.1^{\circ}}(k)\) shows that \(P_{1.1^{\circ}}(k)=(k-3)^2\).
- Calculation of \(P_{1.2^{\circ}}(k)\) shows that \(P_{1.2^{\circ}}(k)=k-3+(k-4)^2\).
We now obtain \begin{eqnarray*} P_{1^{\circ}}(k)&=&2P_{1.1^{\circ}}(k)+(k-3)P_{1.2^{\circ}}(k)\newline &=&2(k-3)^2+(k-3)\left(k-3+(k-4)^2\right)\newline &=&(k-3)\left(2(k-3)+(k-3)+(k-4)^2\right)\newline &=&(k-3)\left(k^2-5k+7\right). \end{eqnarray*}
The polynomial \(\chi_{1^{\circ}}(k)\) can now be obtained using \(P_{1^{\circ}}(k)\).
\begin{eqnarray*} \chi_1^{\circ}&=&k(k-1)(k-2)(k-3)P_{1^{\circ}}(k)\newline &=&k(k-1)(k-2)(k-3)\cdot (k-3)\left(k^2-5k+7\right)\newline &=&k(k-1)(k-2)(k-3)^2\left(k^2-5k+7\right). \end{eqnarray*}Case 2: Calculation of \(\chi_{2^{\circ}}(k)\)
Observe that the vertex \(D\) must have different color from \(A\) and \(C\). Let us denote by \(P_{2^{\circ}}(k)\) the number of colorings of the graph \(\Gamma\) in which the vertex \(A\) has color \(1\), the vertex \(C\) has color \(2\), and the vertex \(D\) has color \(3\). If we cacluate \(P_{2^{\circ}}(k)\) then the polynomial \(\chi_{2^{\circ}}(k)\) satisfies \[\chi_{2^{\circ}}(k)=k(k-1)(k-2)P_{2^{\circ}}(k),\] because there are \(k(k-1)(k-2)\) to pick different colors for the vertices \(A\), \(C\), and \(D\).
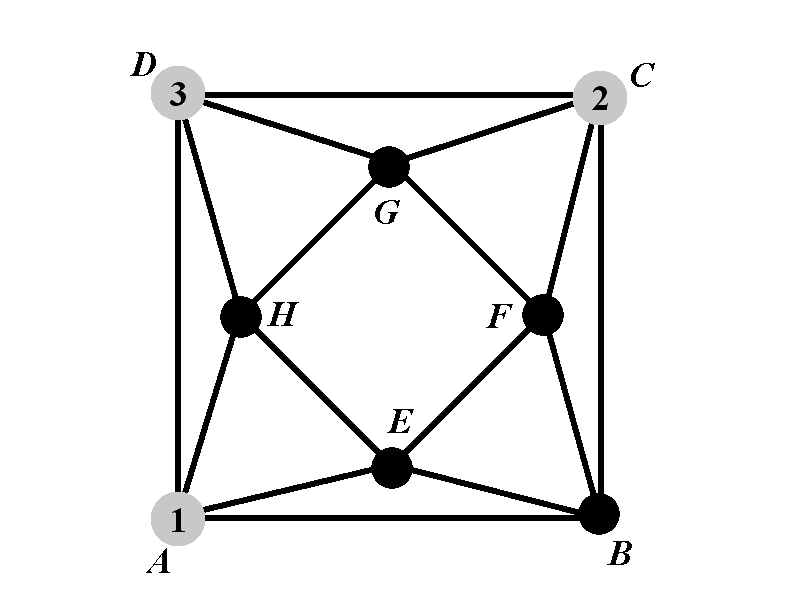
We will now consider two subcases: Subcase \(2.1^{\circ}\) in which the vertex \(B\) has the same color as \(D\) and subcase \(2.2^{\circ}\) in which the vertex \(B\) has color different from \(D\). To make it formal, we introduce the polynomials \(P_{2.1^{\circ}}(k)\) and \(P_{2.2^{\circ}}(k)\) in the following way.
- \(2.1^{\circ}\) Define \(P_{2.1^{\circ}}(k)\) to be the number of proper colorings of \(\Gamma\) with \(k\) colors such that the vertices \(A\), \(B\), \(C\), and \(D\) have colors \(1\), \(3\), \(2\), and \(3\), respectively.
- \(2.2^{\circ}\) Define \(P_{2.2^{\circ}}(k)\) the number of proper colorings of \(\Gamma\) with \(k\) colors such that the vertices \(A\), \(B\), \(C\), and \(D\) have colors \(1\), \(4\), \(2\), and \(3\), respectively.
The polynomial \(P_{2^{\circ}}(k)\) satisfies \[P_{2^{\circ}}(k)=P_{2.1^{\circ}}(k)+(k-3)P_{2.2^{\circ}}(k).\]
- Calculation of \(P_{2.1^{\circ}}(k)\) shows that \(P_{2.1^{\circ}}(k)=(k-3)\left(k^3-9k^2+29k-34\right)\).
- Calculation of \(P_{2.2^{\circ}}(k)\) shows that \(P_{2.2^{\circ}}(k)=(k-3)\left(k^3-9k^2+31k-42\right)\).
Therefore the polynomial \(P_{2^{\circ}}(k)\) satisfies \begin{eqnarray*}P_{2^{\circ}}(k)&=&P_{2.1^{\circ}}(k)+(k-3)P_{2.2^{\circ}}(k)\newline &=&(k-3)\left(k^3-9k^2+29k-34\right)+(k-3)^2\left(k^3-9k^2+31k-42\right)\newline &=&(k-3)\left(k^3-9k^2+29k-34+(k-3)\left(k^3-9k^2+31k-42\right)\right)\newline &=&(k-3)\left(k^4-11k^3+49k^2-106k+92\right). \end{eqnarray*}
The polynomial \(\chi_{2^{\circ}}(k)\) now satisfies \begin{eqnarray*} \chi_{2^{\circ}}(k)&=& k(k-1)(k-2)P_{2^{\circ}}(k)\newline &=&k(k-1)(k-2)(k-3)\left(k^4-11k^3+49k^2-106k+92\right). \end{eqnarray*}
Final Calculation
Now when we have obtained \(\chi_{1^{\circ}}\) and \(\chi_{2^{\circ}}\) we get \begin{eqnarray*}\chi_{\Gamma}(k)&=&\chi_{1^{\circ}}(k)+\chi_{2^{\circ}}(k)\newline &=&k(k-1)(k-2)(k-3)\left((k-3)\left(k^2-5k+7\right)+\left(k^4-11k^3+49k^2-106k+92\right)\right)\newline &=&k(k-1)(k-2)(k-3)\left(k^3-5k^2+7k-3k^2+15k-21+ k^4-11k^3+49k^2-106k+92 \right)\newline &=&k(k-1)(k-2)(k-3)\left(k^4-10k^3+41k^2-84k+71\right). \end{eqnarray*}