Back to: Chromatic Polynomial Case \(2.2^{\circ}\)
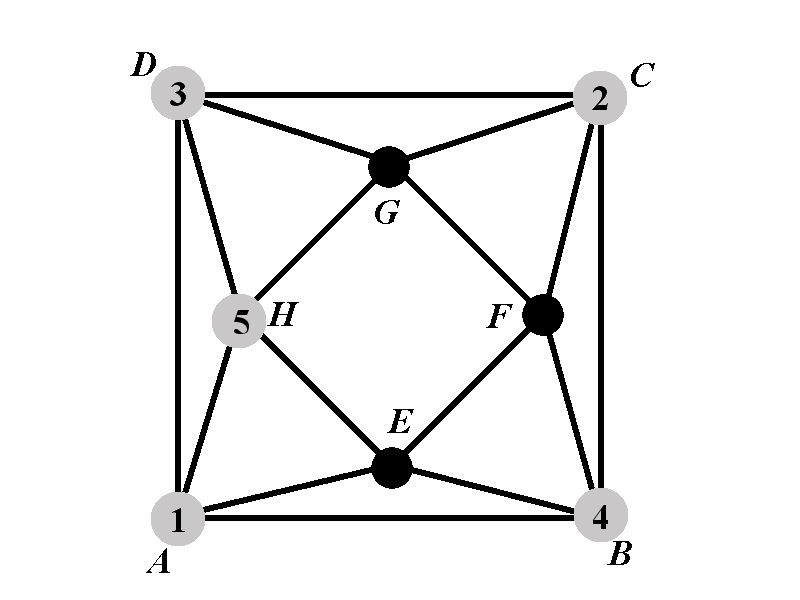
Case 2.2.2: Calculation of \(P_{2.2.2^{\circ}}(k)\)

We will consider cases based on the color of the vertex \(E\). We know that \(E\) can‘t have any of the colors \(1\), \(4\), and \(5\). We will consider 3 cases: Case \(2.2.2.1^{\circ}\) is the one in which \(E\) has color \(2\); Case \(2.2.2.2^{\circ}\) is the one in which \(E\) has color \(3\); and Case \(2.2.2.3^{\circ}\) is the one in which \(E\) has none of the colors from \(\{1,2,3,4,5\}\). We will introduce the following notation:
- \(2.2.2.1^{\circ}\) Denote by \(P_{2.2.2.1^{\circ}}(k)\) the number of proper colorings of \(\Gamma\) in which \(A\), \(B\), \(C\), \(D\), \(E\), and \(H\) have the colors \(1\), \(4\), \(2\), \(3\), \(2\), and \(5\), respectively.
- \(2.2.2.2^{\circ}\) Denote by \(P_{2.2.2.2^{\circ}}(k)\) the number of proper colorings of \(\Gamma\) in which \(A\), \(B\), \(C\), \(D\), \(E\), and \(H\) have the colors \(1\), \(4\), \(2\), \(3\), \(3\), and \(5\), respectively.
- \(2.2.2.3^{\circ}\) Denote by \(P_{2.2.2.3^{\circ}}(k)\) the number of proper colorings of \(\Gamma\) in which \(A\), \(B\), \(C\), \(D\), \(E\), and \(H\) have the colors \(1\), \(4\), \(2\), \(3\), \(6\), and \(5\), respectively.
The number \(P_{2.2.2^{\circ}}(k)\) satisfies \[P_{2.2.2^{\circ}}(k)=P_{2.2.2.1^{\circ}}(k)+P_{2.2.2.2^{\circ}}(k)+(k-5)P_{2.2.2.3^{\circ}}(k).\]
- Calculation of \(P_{2.2.2.1^{\circ}}(k)\) shows that \(P_{2.2.2.1^{\circ}}(k)=k-2+(k-3)(k-4)\).
- Calculation of \(P_{2.2.2.2^{\circ}}(k)\) shows that \(P_{2.2.2.2^{\circ}}(k)=k-3+(k-4)^2\).
- Calculation of \(P_{2.2.2.3^{\circ}}(k)\) shows that \(P_{2.2.2.3^{\circ}}(k)= 2(k-3)+(k-4)(k-5)\).
We can now complete the calculation of \(P_{2.2.2^{\circ}}(k)\).
\begin{eqnarray*} P_{2.2.2^{\circ}}(k)&=&P_{2.2.2.1^{\circ}}(k)+P_{2.2.2.2^{\circ}}(k)+(k-5)P_{2.2.2.3^{\circ}}(k)\newline &=&k-2+(k-3)(k-4)+k-3+(k-4)^2+(k-5)\left(2(k-3)+(k-4)(k-5)\right)\newline &=&k^3-10k^2+36k-47. \end{eqnarray*}