| No. | Title and link |
|---|---|
| 1. | Introduction to C++ |
| 2. | Variables, branching, and loops |
| 3. | Functions and recursions |
| 4. | Pointers |
| 5. | Linked lists |
| 6. | Stacks |
| 7. | Sequences |
| 8. | Pointers practice |
| 9. | References |
| 10. | Sorting |
| 11. | Object oriented programming |
| 12. | Trees in C++ |
| 13. | Balanced trees |
| 14. | Sets and maps: simplified |
| 15. | Sets and maps: standard |
| 16. | Dynamic programming |
| 17. | Multi core programming and threads |
| 18. | Representation of integers in computers |
| 19. | Floating point representation |
| 20. | Templates |
| 21. | Inheritance |
| 22. | Pointers to functions |
| 23. | Reading data from internet |
| 24. | Graphic cards and OpenCL |
| 25. | OpenCL on AWS |
| 26. | OpenCV and optical mark recognition |
12. Binary Search Tree
1. Definition and basic properties
The main ingredient of the tree is a node that has 3 components. The first component is the content. This component is used to store the data. The other two components are the pointers. One contains the addresses of the left child. The other is the address of the right child. We will denote these two addresses by aLeft and aRight.
Of course, these names aLeft and aRight are not mandatory. Often, we will use other names for the addresses of left and right child: aL and aR; or left and right; etc.
Our goal is to make it easy to search for values in the tree. We will make sure that for each node, its content is bigger than the content of every node in the the left sub-tree. Similarly, the content of each node will be smaller than the contents of the nodes in the right sub-tree.
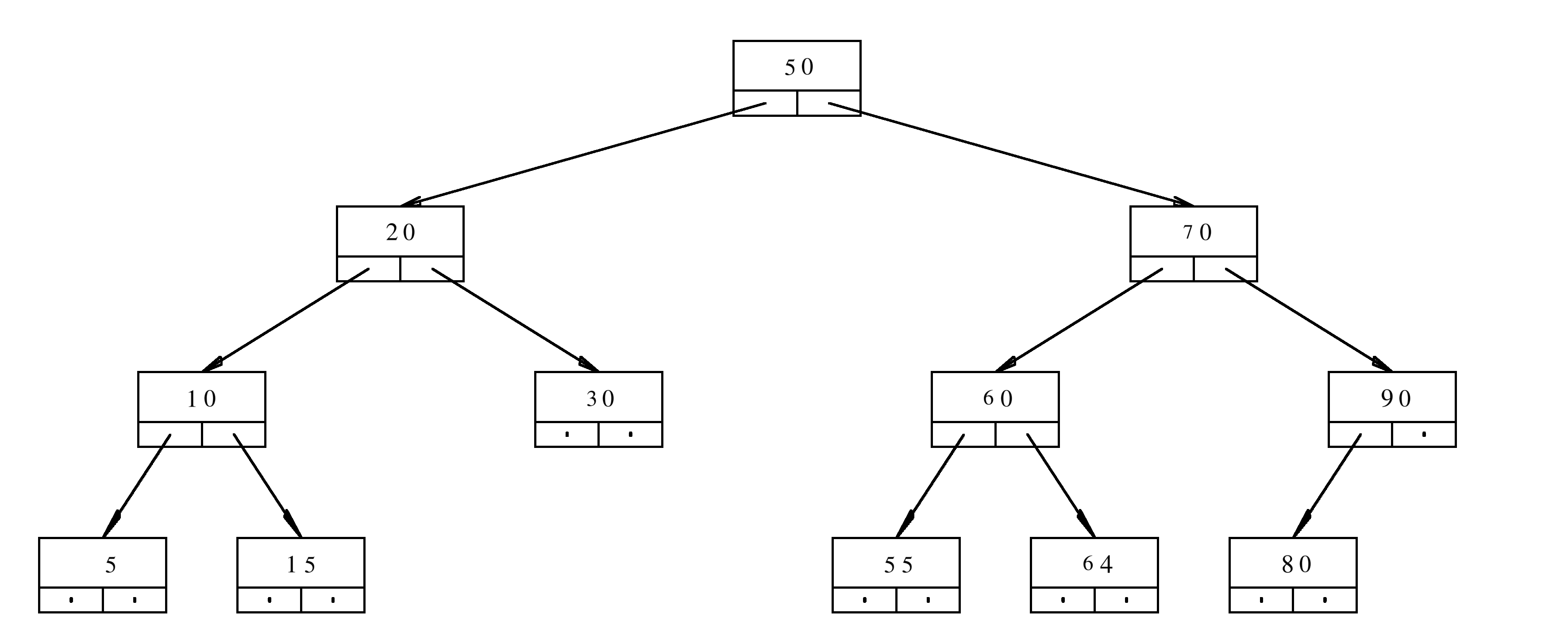
The nodes of the binary tree are declared in the following way:
struct TN{
public:
long cont;
TN* aL;
TN* aR;
};
In this problem you are asked to implement the function valueOfTheRightChild. The function receives the pointer to the root of the tree. The function should return the integer stored in the immediate right child of the root. If the root is nullptr, the function should return -10. If the root is not nullptr, but the right child is nullptr, then the function should return -1. Replace the text // ??? // in the code below to create the function that achieves the desired result.
long valueOfTheRightChild(TN* aRoot){
// ??? //
}
The nodes of the binary search tree are declared in the following way:
struct TN{
public:
long cont;
TN* aL;
TN* aR;
};
Create the function countEvenElements that counts the total number of elements of tree that are even.
Write the code that replaces the text // ??? // below.
long countEvenElements(TN* aRoot){
// ??? //
}
2. Fractions
We will create an example in which the components of the tree are fractions. First, we must create a class that implements the fractions. We will call it Frac. The objects of the class will have two private attributes: numerator and denominator. The class must have the public method operator< that would allow us to compare contents of different nodes. We will then be able to write code of the following nature
Frac a, b;
a.setNum(11); a.setDen(21); b.setNum(111); b.setDen(211);
if(a<b){
std::cout<<"The fraction 11/21 is smaller "
std::cout<<"than the fraction 111/211\n";
}
else{
std::cout<<"The fraction 11/21 is bigger ";
std::cout<<"than or equal to the fraction 111/211\n";
} The execution of the command if(a<b) is the same as the execution of
if( a.operator<(b) ). The method operator< will be applied to the object a. The argument of the method will be the object b
Once we have the comparison operator, we will be able to make a binary search tree whose nodes contain objects of type Frac.
class Frac{
private:
long num; long den;
public:
Frac(const long& =0, const long& =1);
long getNum() const; long getDen() const;
void setNum(const long &);
void setDen(const long &);
int operator< (const Frac& ) const;
};
Frac::Frac(const long & n, const long &d){
num=n;den=d;
if(den==0){den=1;}
if(den<0){den*=-1;num*=-1;}
}
long Frac::getNum() const{return num;}
long Frac::getDen() const{return den;}
void Frac::setNum(const long &n){num=n;}
void Frac::setDen(const long &d){
den=d;
if(den==0){den=1;}
if(den<0){num*=-1;den*=-1;}
}
int Frac::operator< (const Frac & b) const{
if(num*(b.den) < den*(b.num)){return 1;}
return 0;
}
Assume that the class Frac is implemented in the same way as in the notes. Create the function indexOfSmallestFraction with two parameters a and n. The parameter a is the pointer to a block of n consecutive memory locations that contain fractions. The function should return the index i for which the number a[i] is the smallest among the fractions a[0], a[1], ..., a[n-1]. Your code should replace the text // ??? // below.
long indexOfSmallestFraction(Frac* a, long n){
// ??? //
}
3. Implementation of trees
Now that we have created the class Frac we can implement the fundamental functions on the tree: search, insert, and removeElement.
3.1. Function search
3.1.1. Introductory remark
The function search is the easiest to implement. If you are learning trees on your own and implementing all the functions by yourself, then you will have to start with the function insert. Otherwise, you can't build basic trees and test your code.
The autograder will help us here. You will be able to solve some basic exercise before making the full implementation of the tree. These first exercises will ask for very simple tasks. The auto-grader will fill your code with the implementations of insert, search, printTree, and many other useful functions. Then you will be able to see how your submission works when complemented with additional functions provided by the autograder.
3.1.2. Implementation of the function search
The function search receives two arguments: The pointer to the root and the value x that is being searched for.
The function will compare x with the content of the root. If x is smaller, then we need to search the left sub-tree. If x is larger than the content of the root, then we need to search the right sub-tree. If x is neither smaller nor larger than the content of the root, then we have found the required value. The function will return the pointer to the node that contains x, if the value x is found in the tree. Otherwise, if x is not in the tree, then the function will return nullptr.
TNode* search(TNode* aR, const Frac& x){
if(aR==nullptr){
return nullptr;
}
if(x<(aR->content)){
return search(aR->aLeft,x);
}
if( (aR->content) < x){
return search(aR->aRight,x);
}
return aR;
}
Create an implementation of the function countFractionsWithNumerator12 whose parameters are the pointer to the root of the tree aRoot, and two positive integers \(a\) and \(b\) of type long that satisfy \(a< b\). The function should return the total number of fractions from the sequence
\[\frac{12}{a}, \frac{12}{a+1}, \frac{12}{a+2}, \dots, \frac{12}{b-2},\frac{12}{b-1}\] that belong to the tree.
Write the code that replaces the text // ??? // below.
long countFractionsWithNumerator12(TNode* aRoot, long a, long b){
// ??? //
}
The classes Frac and TNode are declared as in the notes. The function search is also implemented in the same way as described. In addition, you may assume that the function insert is implemented and that the pointer aRoot will contain an address to a properly constructed binary search tree.
3.2. Function insert
We will make a recursive function that inserts an element into a tree. Tree is a data structure where recursion is often the best approach. Inserting an element is a great example of why recursion is the best. When you are given a tree, and an element to insert, then you will always be inserting it into one of the subtrees. You will go to the left sub-tree if the value of the new element is smaller than the value in the root; otherwise, you would go to the right subtree.
Now we need to find out the details. Before we can construct the function insert, we must decide what should be the parameters and what should be the return value.
3.2.1. Parameters of the function insert
It is obvious what the parameters should be: The root of the tree and the value that needs to be inserted.
The declaration line of our function will look like this:
***TYPE_OF_THE_RETURN*** insert(TNode* aRoot, Frac value){
// ??? //
}
3.2.2. The return of the function insert
The function will return the address of the new root. Let us see the details by analyzing one example. We are dealing with tree of fractions where the values that are stored look like \(\frac{2}{5}\), \(\frac{1}{30}\), and \(\frac{30}{1}\). For simplicity, we are going to assume that we want to insert the value 30 in the following tree:
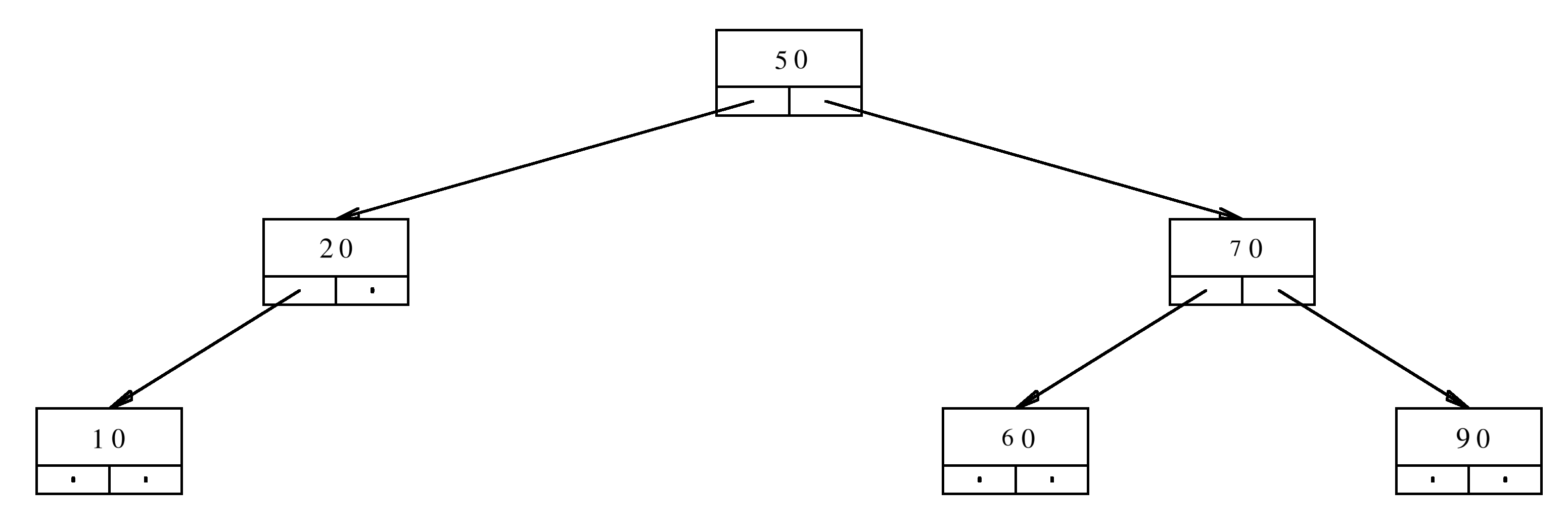
We are going to analyze a recursive call. We need to give the names to different calls of the function. The first call to the function will be labeled Insert 1
When the call Insert 1 is made, it receives the arguments
3.2.2.1. Arguments of Insert 1
aRoot = <address of the node that contains 50> value = 30
Insert 1 will make a call that we will name Insert 2. Since \(30< 50\), the function Insert 1 will pass the arguments aRoot->aLeft and value (which is still 30) to the function Insert 2.
3.2.2.2. Arguments of Insert 2
aRoot = <address of the node that contains 20> value = 30
Insert 2 makes a call that we will name Insert 3. Since \(30> 20\), the function Insert 2 will pass the arguments aRoot->aRight and value (which is still 30) to the function Insert 3.
3.2.2.3. Arguments of Insert 3
aRoot = nullptr value = 30
This time the function needs to insert the node \(30\) in an empty tree. We will create a tree with one node. When this new node is created, the function Insert 2 needs to receive its address. For the purposes of this discussion, let us label that address by addNew.
The address addNew of this newly created node will be used by function Insert 2. In the function Insert 2, the argument aRoot contains the address of the node 20. The right child aRoot->aRight contains nullptr. This value has to be changed from nullptr to addNew.
Consequently, Insert 2 must receive addNew from Insert 3. The easiest way to do this is through return statement. The function insert will always return the address of the root.
The function Insert 3 will transmit an extremely important information to the function Insert 2 with this mechanism. It will transmit the address of the newly created nodes.
Therefore, we the function insert will always return aRoot. The function Insert 2 will also return aRoot to Insert 1. The address that Insert 2 returns to Insert 1 is the same as what Insert 1 sent to Insert 2. Although this may not look like an important exchange of information, the return statement is essential for the deepest recursion in the nest of recursions. In this case, this is the call Insert 3. That call is transferring an essential information to Insert 2.
3.2.3. Implementation of the function insert
TNode* insert(TNode* oldR, const Frac & x){
if(oldR==nullptr){
TNode* nR;
nR=new TNode;
nR->aLeft=nullptr;nR->aRight=nullptr; nR->content=x;
return nR;
}
if(x<(oldR->content)){
oldR->aLeft=addTerm(oldR->aLeft,x);
}
if((oldR->content)<x){
oldR->aRight=addTerm(oldR->aRight,x);
}
return oldR;
}
Create a program that read three fractions a, b, and c, stores these fractions in the tree, and then prints the unique fractions among a, b, and c
Write the code that replaces the text // ??? // below.
int main(){
Frac a,b,c;
long n,d;
std::cin>>n>>d; a.setNum(n); a.setDen(d);
std::cin>>n>>d; b.setNum(n); b.setDen(d);
std::cin>>n>>d; c.setNum(n); c.setDen(d);
TNode* aRoot=nullptr;
// ??? //
printTree(aRoot);
deleteTree(aRoot);
return 0;
}
The classes Frac and TNode are declared as in the notes. The function insert is also implemented in the same way as described. In addition, you may assume that the functions printTree and deleteTree are properly implemented.
3.3. Function removeElement
Removing an element is slightly more challenging to implement than search and insert. We will solve this problem in three steps.
- Step 1. In the first step we will create a function that removes the minimum from the tree. We will call that function
deleteMinimum. - Step 2. In the second step we will create a less powerful function. We will create the function that removes the node only if it does not have the right child. If the node has the right child. We will give the name
removeIfThereIsNoRightChildto this function. If there is the right child of the node, then this function will not be able to achieve the goal. - Step 3. Finally, we will improve the function
removeIfThereIsNoRightChildand turn it into the functionremoveElement. The only modification that we need to make is in the part of the code where we identified thataRootis the node that containsxand thataRoothas the right child. Then we will find the minimum of the right sub-tree; replaceaRoot->contentwith the minimum of the right sub-tree, and then call the functiondeleteMinimumonaRoot->aRight.
Each of the individual steps 1-3 is easy to implement. The code auto-grader will guide you through making your own functions. The auto-grader will help you test your functions on several test cases. In the end of this document, you will be able to see the complete code.
3.3.1. Functions findMinimum and deleteMinimum
Create an implementation of the function findMinimum. The function should return the pointer to the node that contains the minimum of the tree.
Write the code that replaces the text // ??? // below.
TNode* findMinimum(TNode* aRoot){
// ??? //
}
The function should return the minimum of the tree.
Create an implementation of the function deleteMinimum.
Write the code that replaces the text // ??? // below.
TNode* deleteMinimum(TNode* aRoot){
// ??? //
}
The function should return the pointer to the root of the newly obtained tree.
3.3.2. Function removeIfThereIsNoRightChild
Create an implementation of the function removeIfThereIsNoRightChild. The parameters are the pointer aRoot to the root of the tree and the fraction x.
- If
xis not in the tree, the function should do nothing. The function should returnaRootin this case. - If
xis in the tree, and if the node that containsxhas no right child, then the node should be removed. The function should return the pointer to the root of the newly obtained tree. More precisely,xwas not in the root, then the root was unchanged and the function sould return the old root. If, however,xwas in the root, and ifaRoot->aRightwasnullptr, then the root of the tree changes fromaRoottoaRoot->aLeft. The function should return this new root. - If
xis in the tree, but the node that containsxhas the right child, then the function should do nothing. The function should return the address of the rootaRootthat it received.
Write the code that replaces the text // ??? // below.
TNode* removeIfThereIsNoRightChild(TNode* aRoot, Frac x){
// ??? //
}
3.3.3. Function removeElement
Create an implementation of the function removeElement. The parameters are the pointer aRoot to the root of the tree and the fraction x.
The code below already has the parts of the function that treat the cases when aRoot is a null pointer, and when x is not the same as aRoot->content. The code provided by auto-grader also includes the treatment of the cases in which the node with x has no right child.
Therefore, it only remains to write the code in which we are already certain that x is the same as aRoot->content and aRoot->aRight!=nullptr.
Write the code that replaces the text // ??? // below.
TNode* removeElement(TNode* aRoot, const Frac & x){
if(aRoot==nullptr){
return nullptr;
}
if(x<(aRoot->content)){
aRoot->aLeft=removeElement(aRoot->aLeft,x);
return aRoot;
}
if((aRoot->content)<x){
aRoot->aRight=removeElement(aRoot->aRight,x);
return aRoot;
}
// We found out that aRoot->content is equal to x
// Check if the right sub-tree is empty
if(aRoot->aRight==nullptr){
TNode* nR=aRoot->aLeft;
delete aRoot;
return nR;
}
// ??? //
}
You are allowed to use the functions deleteMinimum and findMinimum.
4. Complete implementation for tree of fractions
// treeExamples.cpp
// compile with
// c++ treeExamples.cpp -o tExamples -std=c++11
// execute with
// ./tExamples
//
#include<iostream>
// Place here the declaration and implementation of the class Frac
class TNode{
public:
Frac content;
TNode* aLeft;
TNode* aRight;
};
TNode* insert(TNode* oldR, const Frac & x){
if(oldR==nullptr){
TNode* nR;
nR=new TNode;
nR->aLeft=nullptr;nR->aRight=nullptr; nR->content=x;
return nR;
}
if(x<(oldR->content)){
oldR->aLeft=insert(oldR->aLeft,x);
}
if((oldR->content)<x){
oldR->aRight=insert(oldR->aRight,x);
}
return oldR;
}
TNode* search(TNode* aR, const Frac& x){
if(aR==nullptr){
return nullptr;
}
if(x<(aR->content)){
return search(aR->aLeft,x);
}
if( (aR->content) < x){
return search(aR->aRight,x);
}
return aR;
}
TNode* findMinimum(TNode* aR){
if(aR==nullptr){
return nullptr;
}
if(aR->aLeft==nullptr){
return aR;
}
return findMinimum(aR->aLeft);
}
TNode* deleteMinimum(TNode* aR){
if(aR==nullptr){
return nullptr;
}
if(aR->aLeft==nullptr){
TNode* nRoot;
nRoot=aR->aRight;
delete aR;
return nRoot;
}
aR->aLeft=deleteMinimum(aR->aLeft);
return aR;
}
TNode* removeElement(TNode* aRoot, const Frac & x){
if(aRoot==nullptr){
return nullptr;
}
if(x<(aRoot->content)){
aRoot->aLeft=removeElement(aRoot->aLeft,x);
return aRoot;
}
if((aRoot->content)<x){
aRoot->aRight=removeElement(aRoot->aRight,x);
return aRoot;
}
// We found out that aRoot->content is equal to x
// Check if the right sub-tree is empty
if(aRoot->aRight==nullptr){
TNode* nR=aRoot->aLeft;
delete aRoot;
return nR;
}
// If the right sub-tree is not empty, then pick the smallest
// member of the right subtree.
TNode* aMin=findMinimum(aRoot->aRight);
// Place aMin->content into aRoot->content
aRoot->content=aMin->content;
// Delete the minimum from the right subtree
aRoot->aRight=deleteMinimum(aRoot->aRight);
return aRoot;
}
void printTree(TNode* root,const int& height = 0){
if(root!=nullptr){
printTree(root -> aLeft,height+1);
std::cout << "\t" << (root->content).getNum();
std::cout << "/" << (root->content).getDen();
std::cout << " (" << height << ")";
printTree(root-> aRight,height+1);
if(height==0){
std::cout << std::endl;
}
}
}
void deleteTree(TNode* aRoot){
if(aRoot==nullptr){return;}
deleteTree(aRoot->aLeft);
deleteTree(aRoot->aRight);
delete aRoot;
}
Frac readFraction(){
std::cout << "Insert numerator and denominator. ";
Frac f;
long num,den;
std::cin >> num >> den;
f.setNum(num);f.setDen(den);
return f;
}
std::string menu(){
std::string m;
m+="-1.\t Exit.\n";
m+="0.\t Print menu.\n";
m+="1.\t Insert a fraction in the tree.\n";
m+="2.\t Check whether a fraction is in the tree.\n";
m+="3.\t Delete a fraction from the tree.\n";
m+="4.\t Print all elements of the tree from smallest to largest.\n";
return m;
}
int main(){
TNode* theRoot;
theRoot=nullptr;
std::string choice;
std::cout<<menu();
std::cout<<">> ";
std::cin>>choice;
while(choice!="-1"){
if(choice=="0"){
std::cout<<menu();
}
Frac frInput;
if((choice=="1")||(choice=="2")||(choice=="3")){
frInput=readFraction();
}
if(choice=="1"){
theRoot=insert(theRoot,frInput);
}
if(choice=="2"){
TNode* check=search(theRoot,frInput);
if(check==nullptr){
std::cout << "Not found.\n";
}
else{
std::cout << "The fraction "<< frInput.getNum()<<"/";
std::cout << frInput.getDen()<< " is in the tree.\n";
}
}
if(choice=="3"){
theRoot=removeElement(theRoot,frInput);
}
if(choice=="4"){
printTree(theRoot);
}
std::cout<<">> ";
std::cin>>choice;
}
deleteTree(theRoot);
theRoot=nullptr;
return 0;
}
5. Practice problems
Assume that the class Frac is implemented in the same way as in the notes. The tree node is declared with
class TNode{
public:
Frac content;
TNode* aLeft;
TNode* aRight;
};
Create the function printFromLargestToSmallest whose parameter is the root of the tree. The function should print all the fractions in decreasing order. The functions should be printed as num/den with single space character between them. Your code should replace the text // ??? // below.
void printFromLargestToSmallest(TNode* aRoot){
// ??? //
}
The nodes of the binary search tree are declared in the following way:
struct TN{
public:
long cont;
TN* aL;
TN* aR;
};
Create the function eraseRootAndSplit that removes the root of the binary search tree and splits the tree into two: left sub-tree and right sub-tree. The function has three parameters. The first parameter is aRoot that points to the root of the tree. The other two parameters are references to pointers. They are aLeftSubtree and aRightSubtree. The function should store the addresses of the roots of two subtrees in aLeftSubtree and aRightSubtree
Write the code that replaces the text // ??? // below.
void eraseRootAndSplit(TN* aRoot, TN*& aLeftSubtree, TN*& aRightSubtree){
// ??? //
}