| No. | Title and link |
|---|---|
| 1. | Introduction to C++ |
| 2. | Variables, branching, and loops |
| 3. | Functions and recursions |
| 4. | Pointers |
| 5. | Linked lists |
| 6. | Stacks |
| 7. | Sequences |
| 8. | Pointers practice |
| 9. | References |
| 10. | Sorting |
| 11. | Object oriented programming |
| 12. | Trees in C++ |
| 13. | Balanced trees |
| 14. | Sets and maps: simplified |
| 15. | Sets and maps: standard |
| 16. | Dynamic programming |
| 17. | Multi core programming and threads |
| 18. | Representation of integers in computers |
| 19. | Floating point representation |
| 20. | Templates |
| 21. | Inheritance |
| 22. | Pointers to functions |
| 23. | Reading data from internet |
| 24. | Graphic cards and OpenCL |
| 25. | OpenCL on AWS |
| 26. | OpenCV and optical mark recognition |
24. Parallel Programming on Graphic Cards Using C++ and OpenCL
Source codes
The source codes and classes are contained in the following archive
Installation of drivers and libraries
Although the computer hardware is capable for supporting OpenCL for majority of systems produced after 2010, it is sometimes necessary to install the appropriate drivers.
The following commands will install the necessary drivers and libraries on the official laptops for the course:
sudo apt install ocl-icd-libopencl1 sudo apt install opencl-headers sudo apt install clinfo sudo apt install ocl-icd-opencl-dev sudo apt install beignet
More details can be found at http://askubuntu.com/questions/850281/opencl-on-ubuntu-16-04-intel-sandy-bridge-cpu
Introduction
GPGPU
The abbreviation GPGPU refers to general purpose programming on graphics processing units. The graphic cards of modern computers can be used to do serious scientific calculations. They contain thousands of computing cores (that we will call processing elements), and as such they are ideal for parallel programming. The processing elements can be thought of as small CPUs that are numerous, but not as advanced as the central processors. High end CPUs can have speeds in range of 4GHz, but a quad-core system will have only four of these units. On the other hand, the graphic card can have 4000 processing elements each of which runs at 1GHz. In addition, not all operations are permitted and not all data structures are available to the processing elements of a typical graphic card.
Class GraphicCard
The interaction between GPU and the host platform is fairly complex for the beginners. This tutorial introduces the class GraphicCard written in C++ which does most of the work associated with memory management on GPU. The usage of this class removes the necessity of understanding completely the mechanisms on how platforms, contexts, devices, kernels, workgroups, and memory objects are related to each other.
Needless to say, the usage of this class is limited to building the basic codes only. It is unlikely that the class will be suitable for projects that need to harness the full power of parallel programming on GPUs. A comprehensive coverage of OpenCL is provided in the book "OpenCL Programming guide" by A. Munshi, B. Gaster, T.G. Mattson, J. Fung, and D. Ginsburgat.
CPU, GPU, RAM, and device memory
In the course of introducing the necessary terminology we will frequently refer to the first problem we have the intention to solve:
Read the sequence \(\overrightarrow a= (a[0]\), \(a[1]\), \(\dots\), \(a[n-1])\) from a file on the hard disk and update it to obtain \(a[k]:=2 \ast a[k]\) for each \(k\in\{0,1,\dots, n-1\}\).
The main idea in solving this problem is to assign each term of the sequence \(\overrightarrow a\) to a specific processing element on a graphic card. This way one processing element will perform the operation \(a[0]:=2\ast a[0]\). At the same time another element will perform \(a[1]:=2\ast a[1]\), and so on.
The programmer may always assume that the number of processing elements is as large as necessary. When the shortage of resources occurs, the compiler will simply assign a single processing element to multiple tasks that will not be performed in parallel. The C++/OpenCL code does not have to be aware of that.
Organization of the hardware
For the purposes of this tutorial the computer hardware can be thought to consist of the following two units:
- Host - A traditional computing system that consists of CPU and RAM memory. Host programs are written in C++.
- Device - A graphic card that consists of a GPU with thousands of processing elements, and its own memory that we will call device memory. Programs that can be run on processing elements are called kernels and are written in OpenCL.
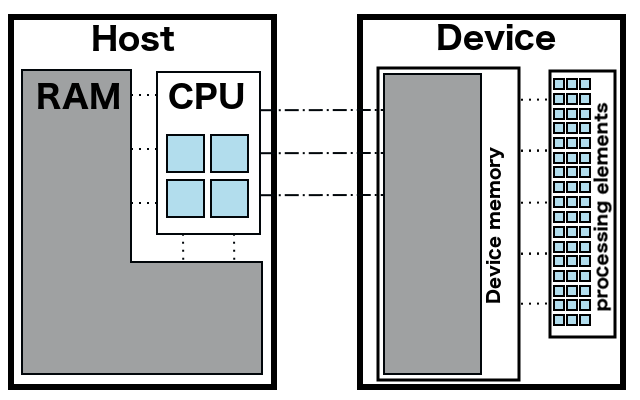
The processing elements have access to the device memory only. Specifically, they cannot access the RAM memory on the host. On the other hand, the CPU can access its RAM memory, and can perform basic copying of elements from RAM to device memory and vice versa. However, one should always keep in mind that communication between CPU and device memory is not as fast as the communication between the processing elements and the device memory.
Traditional programs written in C++ organize complicated data structures within the RAM memory. In contrast, sequences are the only data structures that are permitted on device memory.
Program organization
Each program that uses graphic cards has the following main components: Kernels, which are run on GPU processing elements and are written in OpenCL; and Host, which is run on CPU and is written in C++.
Solving our first problem consists of the following tasks:
- Reading the sequence \(\overrightarrow a\) from a file. This task must be performed by host. The processing elements do not have the ability to access the hard disk on which the file is located.
- Copying the sequence \(\overrightarrow a\) from RAM to device memory. This task has to be performed by host as well.
- Executing the kernels. The host will specify how many processing elements will be deployed in executing the kernel, and will synchronize the execution. The processing elements work in parallel on the same kernel code and have access to the same sequence on the device memory. The only differentiating factor between the kernels is their ID number. Each kernel will receive a different ID and our program will be designed to use this ID as an index of sequence. This way the kernel with ID \(27\) will perform the task \(a[27]=2\ast a[27]\), while the one with the ID \(17\) will perform the task \(a[17]=2\ast a[17]\).
- Reading the result from the device memory to the host memory. This operation will be performed by the host.
Reading sequences from files
Our goal is to get to OpenCL programming as soon as possible and in order to do this we will use a pre-made program that can read the sequence \(\overrightarrow a\) from the file input.txt and store it in the RAM memory. The code in generatingSequenceFromFile.cpp contains two important functions: readSequenceFromFile and printToFile.
Please go over the simple code from the file gcard_example00.cpp. It explains how the sequence is read from the input file, stored in the memory and the written to the hard-disk using printToFile.
The input file input00.txt contains the sequence that is to be read by the program. Integers (and minus signs) are treated as input, while everything else is ignored. The first number in the file is the length \(n\) of the sequence. The remaining numbers are the elements, until the number \(-9\) is reached. This number \(-9\) is not included in the sequence, but all the remaining terms (and there has to be a total of \(n\) terms) are generated at random.
Multiplying each term of sequence by 2
In this section we will develop our first program that solves Problem 1. We will multiply each term of the sequence \(\overrightarrow a\) by \(2\).
Designing the kernel
Our intention is for each processing element to work on one term of the sequence. get_global_id(0) is an OpenCL command that provides the processing element with the information on which ID number is assigned to it. Once this information is obtained the task is obvious, and we may summarize this with the following code:
myint index = get_global_id(0); a[index]=2*a[index];
There is one one unpleasant surprise coming from the design of the GPU hardware. The host program (run on CPU) cannot request any number of processing elements. The architecture of GPU groups these elements and the members of each group have to be invoked together. Typically, NVIDIA hardware has groups of size 32 while AMD has groups of size 64. These particular numbers are something that is supposed to be ignored by those wishing to write elegant programs. However, it is dangerous to forget the fact that the host is almost always going to receive more processing elements than it has asked for.
In particular, the previous two lines of code may result in a disaster: If the sequence \(\overrightarrow a\) has \(57\) terms and the host asks for the kernel to be run on \(57\) processing elements, the host will actually receive \(64\) of processing elements. One unfortunate processing element will receive the id \(60\) and consequently will try to access \(a[60]\), which is not a memory that should be accessed. One way to prevent the described difficulty is to supply each processing element with the information on the length of the sequence, and the code becomes:
myint index = get_global_id(0);
if(index<lengthOfTheSequence){
a[index]=2*a[index];
}
We have now finished designing the algorithm that will be run on device. It remains to create the file parallel01.cl with the following code:
// parallel01.cl
__kernel void eachTermGetsDoubled(__global myint* a,
__global myint* n)
{
myint index = get_global_id(0);
if(index<*n){
a[index]=a[index]*2;
}
}
The word __kernel must be used before the declaration of kernel. The kernel must not return anything because there is no mechanism for CPU to accept parallel returns of thousands of kernels. Thus, the function type must be \verb+void+. The name we have chosen for our kernel is eachTermGetsDoubled.
Then we list our arguments. The arguments are data structures that are located on the device memory. They must be sequences. In C++ sequences and pointers are related, and sequence a is a variable of type int*. The length of a has to be supplied to the processing elements and this task is accomplished by providing an additional argument to the kernel. Since this argument must be a sequence, we are forced to have n of type int*. We will not go into details on what does __global mean.
Designing the program on the host
The source of the host program is gcard_example01.cpp. The host first reads the input sequence from the file input01.txt in the way that was described above. The sequence will be stored in aRAM. The host will also learn the length of the sequence and this information will be kept by the variable nRAM. The host will then create an objectmyCard that will handle the communication with the graphic card and the synchronizations between processing elements. This is achieved with the command
GraphicCard myCard("parallel01.cl");
Immediately after its creation the object myCard allows us to create the memory on the device in which the sequence a will be stored.
myCard.writeDeviceMemory("a",aRAM,nRAM);
The function writeDeviceMemory creates a sequence on the device. The first argument specifies the name by which this sequence will be referred to in future. The kernel can now use this name in its arguments to access the sequence. The second argument is the sequence in RAM whose content will be copied to the device, and the third argument specifies the length of the sequence on the device.
The device memory also needs to contain the information on how long the sequence \(\overrightarrow a\) is, which is stored in nRAM. We will use the function writeDeviceMemory again. The first argument will be "n" since our kernel expects this name to be used for the length of the sequence. The second argument must be some kind of a sequence. The problem is that nRAM is not a sequence. It is an integer. However, &nRAM is a pointer to integer, which in C++ is the same as sequence of length 1. The last, third argument of writeDeviceMemory is the length of the sequence &nRAM and this length is \(1\). In summary, we will be calling the function by
myCard.writeDeviceMemory("n",&nRAM,1);
The kernel can be now executed using nRAM processing elements. This is accomplished with the command:
myCard.executeKernel("eachTermGetsDoubled",nRAM);
The execution will modify the sequence a. Each of its terms will be multiplied by 2, and the result will be stored in a again. However, the sequence a is located on the device, not in the RAM memory. The retrieval is obtained using the following code
myint* resultRAM;
resultRAM=new myint[nRAM];
myCard.readDeviceMemory("a",resultRAM,nRAM);
After these lines of code, the sequence resultRAM contains the desired outcome. We can summarize our code with the following listing
// gcard_example01.cpp
//A program that takes a sequence from the input file and doubles each of its elements.
// compile with
// c++ -o gcard_ex01 gcard_example01.cpp -lOpenCL -std=c++11
// execute with
// ./gcard_ex01
#define CL_USE_DEPRECATED_OPENCL_1_2_APIS
#include <iostream>
#include <fstream>
#include "GraphicCardOpenCL.cpp"
#include "generatingSequenceFromFile.cpp"
int main(){
myint *aRAM;
myint nRAM;
readSequenceFromFile("input01.txt", &aRAM, &nRAM );
// Allocate an object myGPU that is of the type GraphicCard
// myGPU object will contain the kernel written in parallel01.cl
GraphicCard myGPU("parallel01.cl");
// We will place the sequence aRAM to the device memory.
// The kernel will look for a sequence "a" on the device memory.
// We will create this sequence by copying the sequence aRAM from the host memory.
myGPU.writeDeviceMemory("a",aRAM,nRAM);
// Similarly, we need to place the variable "n" on the graphic card.
// Since the only allowed objects on the graphic cards are sequences, and n is
// a single element, it must be treated as an one-element sequence.
// Luckily, in C++ every pointer is an one-element sequence, and so is &nRAM.
myGPU.writeDeviceMemory("n",&nRAM,1);
// The GPU is given instruction to execute the kernel on at least nRAM processing elements.
// Caution: GPU may actually invoke more than nRAM elements, and you can‘t control this.
// Hardware design of GPU organizes the processing elements in groups and only the entire
// group can be called.
myGPU.executeKernel("eachTermGetsDoubled",nRAM);
// After the kernel execution we need to retrieve the new modified sequence "a".
// The sequence has to be copied from the device memory back to the RAM memory.
// We can accomplish this by first creating the space in RAM sufficient to store the new sequence.
myint * resultRAM;
resultRAM=new myint[nRAM];
// Now since the space is created, we call the function that reads the content of the
// device memory and stores it in the sequence resultRAM.
myGPU.readDeviceMemory("a",resultRAM,nRAM);
//The final step is to output the result in the file output.txt
std::ofstream fOutput;
fOutput.open("output01.txt");
myint mLen=nRAM;
if(mLen>30){mLen=30;}
for(myint i=0;i<mLen;i++){
fOutput<<resultRAM[i]<<" ";
}
fOutput<<std::endl;
fOutput.close();
delete [] aRAM;
delete [] resultRAM;
return 1;
}
Memory management
In this section we will consider a more advanced problem that will illustrate one famous trap that occurs in designing parallel algorithms. The difficulty is referred to as memory race and it appears when one processing element is attempting to write to a memory location that the other processing element is reading from. Let us consider the following problem:
The sequence \(\overrightarrow a= (a[0]\), \(a[1]\), \(\dots\), \(a[n-1])\) is stored in a file on the hard disk. The operation \(X\) is defined on sequences in such a way that it takes a sequence \(\overrightarrow s\) of length \(n\) as an input and produces an entire sequence \(\overrightarrow t = X\left(\overrightarrow s\right)\) of length \(n\) as an output. The terms of the sequence \(\overrightarrow t\) are defined as \(t[k]=s[k]+2\ast s[k+1]\) if \(k < n-1\), and \(t[n-1]=s[n-1]\). The operation \(X\) can be defined using precise mathematical language: \[X\left(\overrightarrow s\right)[k]=\left\{\begin{array}{rl}s[k]+2\ast s[k+1],&\mbox{if }k < n-1\newline s[k],&\mbox{if }k=n-1.\end{array}\right.\] Another operation \(Y\) is also defined on sequences in the following way: \[Y\left(\overrightarrow s\right)[k]=\left\{\begin{array}{rl}s[k]+3\ast s[k-1],&\mbox{if }k > 0\newline s[k],&\mbox{if }k=0.\end{array}\right.\] The sequence \(w[0]\), \(w[1]\), \(\dots\), \(w[m-1]\) is entered through standard input.
The goal of the program is to replace the sequence \(\overrightarrow a\) with a new sequence in each of \(m\) consecutive iterations. In the first iteration, if \(w[0]=0\) then \(\overrightarrow a\) should be replaced by \(X\left(\overrightarrow a\right)\). However, if \(w[0]=1\), then \(\overrightarrow a\) should be replaced by \(Y\left(\overrightarrow a\right)\). In the \(j\)-th iteration (for \(j\in\{0,1,\dots, m-1\}\)), the sequence \(\overrightarrow a\) should be replaced by \(X\left(\overrightarrow a\right)\) if \(w[j+1]=0\), or by \(Y\left(\overrightarrow a\right)\) if \(w[j+1]=1\). The output of the program should be the final state of \(\overrightarrow a\).
To make sure that the problem is correctly understood, let us consider the sequence \(\overrightarrow a\) of length \(5\) with the terms \((-2,3,0,1,1)\). Let us assume that there will be \(m=3\) iterations and that \(w[0]=0\), \(w[1]=1\), and \(w[2]=1\). Then in the first iteration, the value \(w[0]=0\) is used to determine that the sequence \(\overrightarrow a\) should be replaced by the sequence \begin{eqnarray*}X\left(\overrightarrow a\right)&=&X(-2,3,0,1,1)\newline&=& \left(a[0]+2\ast a[1], a[1]+2\ast a[2], a[2]+2\ast a[3], a[3]+2\ast a[4],a[4]\right)\newline &=&\left(4,3,2,3,1\right). \end{eqnarray*} In the next iteration we will use that \(w[1]=1\) and replace \(\overrightarrow a\) with \( Y\left(\overrightarrow a\right)=Y\left(4,3,2,3,1\right)= \left(4,15,11,9,10 \right). \) In the final iteration we will replace the new \(\overrightarrow a\) with \(Y\left(\overrightarrow a\right)\) because \(w[2]=1\). The final outcome of the described sequence of operations should be the sequence \(\overrightarrow a\) that contains the terms \(Y\left(\overrightarrow a\right)=Y \left(4,15,11,9,10 \right)=\left(4,27,56,42,37\right). \)
For solving this problem we will introduce two kernels: one for operation \(X\) and another for operation \(Y\). Then we will run a for loop on the host system and depending on whether the corresponding \(w[i]\) is \(0\) or \(1\) we will call either the kernel \(X\) or the kernel \(Y\).
An undesirable kernel that would result in a memory race
We will first implement a naive approach to building the kernel for the operation \(X\). If we try to recycle our old code and modify it slightly we would end up with something like:
__kernel void X(__global myint* aSeq, __global myint* n){
myint index = get_global_id(0);
if(index<*n){
if(index< (*n)-1){
aSeq[index]=aSeq[index]+2*aSeq[index+1];
}
}
}
We will now consider the effects of applying the previous kernel to the sequence \(\overrightarrow a=\left(-2,3,0,1,1\right)\). Let us analyze the behaviors of the processing elements that get assigned the IDs \(1\) and \(2\). We will label these two processing elements with \(PE1\) and \(PE2\). \begin{eqnarray*} \begin{array}{|c|c|c|c|c|c|} \hline \overrightarrow a & -2 & \;\;\;3 & \;\;\;0 & \; \;\;1 & \; \;\;1 \newline \hline X\left(\overrightarrow a\right) & &PE1&PE2 & & \newline \hline\end{array} \end{eqnarray*}
The processing element \(PE1\) is doing the operation \(a[1]:=a[1]+2a[2]\), and the correct result that \(PE1\) should obtain is \(3+2\cdot 0=3\). In the same kernel execution, the processing element \(PE2\) is calculating \(a[2]:=a[2]+2a[3]\). If by any chance the element \(PE2\) finishes the calculation before the element \(PE1\) has started, then the value stored in \(a[2]\) will no longer be \(0\), but \(2\) instead. The evaluation that \(PE1\) performs will end in tragedy. The value of \(a[1]\) will be \(3+2\cdot 2=7\), instead of \(3\).
One may ask "Is this really a problem?" -- the processing elements are working simultaneously. Well, this simultaneous work is not guaranteed. They may be working simultaneously, but there are many situations in which that would not be the case. For example, if the number of processing elements that the host requests is larger than the number of available elements, than some elements will get several tasks assigned to them. The order in which they choose to execute the tasks may not be the one that the programmer had in mind.
Memory race avoidance
We have to make sure that the processing elements are not writing to the locations from which some other processing elements could be reading. In this particular example this could be avoided by using another sequence \(\overrightarrow b\) to which the processing elements will write while executing the kernel \(X\). The updated kernel \(X\) becomes:
__kernel void X(__global myint* aSeq, __global myint* bSeq, __global myint* n){
myint index = get_global_id(0);
if(index<*n){
if(index< (*n)-1){
bSeq[index]=aSeq[index]+2*aSeq[index+1];
}
else{
bSeq[index]=aSeq[index];
}
}
}
In a similar way we construct the kernel \(Y\).
__kernel void Y(__global myint* aSeq, __global myint* bSeq, __global myint* n){
myint index = get_global_id(0);
if(index<*n){
if(index>0){
bSeq[index]=aSeq[index]+3*aSeq[index-1];
}
else{
bSeq[index]=aSeq[index];
}
}
}
These modifications in the kernel will have one consequence that would require a few more lines of code. The sequence \(\overrightarrow b\) will have the values that we intended to assign to \(\overrightarrow a\). One remedy for this small trouble is to add one more kernel that copies the sequence \(\overrightarrow b\) to sequence \(\overrightarrow a\). This new kernel will be called after each execution of \(X\) or \(Y\).
__kernel void copyBtoA(__global myint* aSeq, __global myint* bSeq, __global myint* n){
myint index = get_global_id(0);
if(index<*n){
aSeq[index]=bSeq[index];
}
}
If the previous three kernels are saved in the file parallel02.cl we can write the following program in gcard_example02.cpp:
// gcard_example02.cpp
// compile with
// c++ -o gcard_ex02 gcard_example02.cpp -lOpenCL -std=c++11
// execute with
// ./gcard_ex02
#define CL_USE_DEPRECATED_OPENCL_1_2_APIS
#include <iostream>
#include <fstream>
#include "GraphicCardOpenCL.cpp"
#include "generatingSequenceFromFile.cpp"
int main(){
std::ofstream fOutput;
fOutput.open("output02.txt");
myint *aR;
myint *wR;
myint nRAM;
myint m;
std::cout << "How long is the array w?" << std::endl;
std::cin >> m;
std::cout << "Enter array of "<<m <<" elements - 0 or 1 please" << std::endl;
wR = new myint[m];
for (int j=0; j<m; j++) {
std::cout<<"Enter the "<<j<<"th element. ";
std::cin >> wR[j];
}
readSequenceFromFile("input02.txt", &aR, &nRAM );
GraphicCard myCard("parallel02.cl");
myCard.writeDeviceMemory("aSeq",aR,nRAM);
myCard.writeDeviceMemory("bSeq",aR,nRAM);
myCard.writeDeviceMemory("n",&nRAM,1);
for (myint k=0; k < m; k++) {
if (wR[k] == 0) {
std::cout<<"Executing kernel X"<<std::endl;
myCard.executeKernel("X",nRAM);
myCard.executeKernel("copyBtoA",nRAM);
}
else {
std::cout<<"Executing kernel Y"<<std::endl;
myCard.executeKernel("Y",nRAM);
myCard.executeKernel("copyBtoA",nRAM);
}
}
myint * resultRAM;
resultRAM=new myint[nRAM];
myCard.readDeviceMemory("aSeq",resultRAM,nRAM);
myint mLen=nRAM;
if(mLen> 30){mLen=30;}
for(myint i=0;i< mLen;i++){
fOutput<< resultRAM[i]<< " ";
}
fOutput<< std::endl;
fOutput.close();
delete [] aR;
delete [] resultRAM;
return 1;
}