| 1. | Interview brainteasers 1 |
| 2. | Interview brainteasers 2 |
| 3. | Interview brainteasers 3 |
| 4. | Interview brainteasers 4 |
| 5. | Combinatorial geometry |
| 6. | Multiplayer games |
Brainteasers from Interviews - Part 1
150 Most Frequently Asked Questions on Quant Interviews
by Dan Stefanica, Rados Radoicic, and Tai-Ho Wang, second edition, FE Press 2019, 281 pages
Probability and Stochastic Calculus Quant Interview Questions
by Ivan Matic, Rados Radoicic, and Dan Stefanica, FE Press 2021, 334 pages
Challenging Brainteasers for Interviews
by Rados Radoicic, Ivan Matic, and Dan Stefanica, FE Press 2023, 345 pages
Problem 1. Bob is a witty trader who trades exotic fruit grown far away.
He travels from one place to another with three sacks which can hold \(30\) fruits each. None of the sacks can hold more than \(30\) fruits.
He starts with \(30\) fruits in each sack.
On his way, he must pass through \(30\) checkpoints,
and at each checkpoint he has to give one fruit for each sack to the authorities.
How many fruits remain after he goes through all the \(30\) checkpoints?
Problem 2. Four players sit in a circle on chairs numbered clockwise
from \(1\) to \(4\).
Each player has two hats, one black and one white,
and is wearing one and holding the other.
In the center sits a fifth player who is blindfolded.
That player designates the chair numbers
of those whose hats should be changed.
His goal is to get all four wearing a hat of the same color,
in which case the game stops.
Otherwise,
after each guess, the four walk clockwise past an arbitrary number of chairs (maintaining the same cyclic order),
then sit for the next guess.
Find a strategy that always works for the blindfolded player.
Problem 3. How many times do I have to roll a die on average until I roll the same number six times in a row?
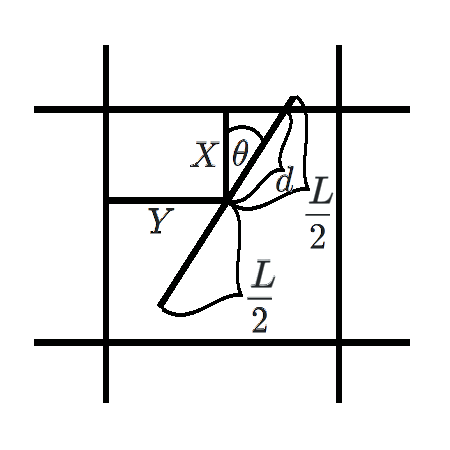
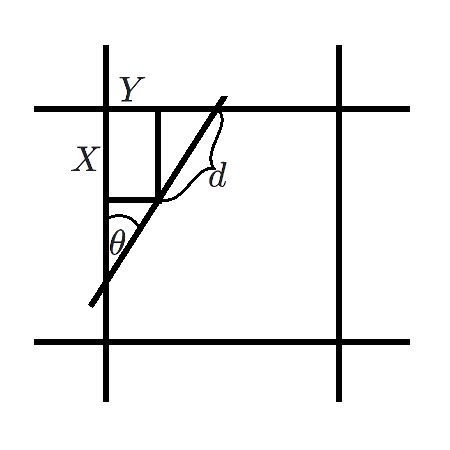
Problem 4. An infinite sheet of paper has inscribed on it a set of horizontal lines \(D\) units apart and a set of vertical lines \(D\) units apart. A needle of length \(L\) (where \(L < D\)) is twirled and tossed on the paper. What is the expected number of lines crossed by the needle? What is the probability that the needle crosses a line?
Problem 5. In how many ways can you divide \(7\) candies and \(14\) stickers among \(4\) children
such that each child gets at least one candy
and also gets more stickers than candies?