| 1. | Interview brainteasers 1 |
| 2. | Interview brainteasers 2 |
| 3. | Interview brainteasers 3 |
| 4. | Interview brainteasers 4 |
| 5. | Combinatorial geometry |
| 6. | Multiplayer games |
Puzzles in Geometry and Combinatorial Geometry
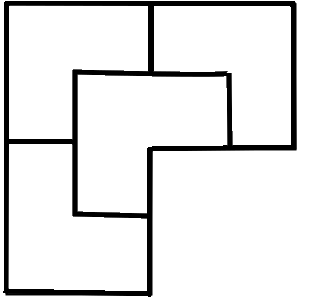
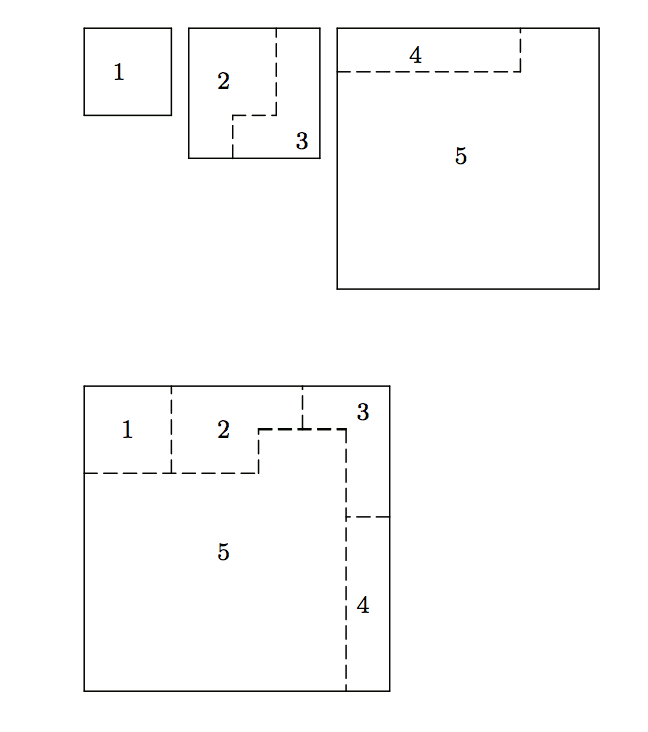
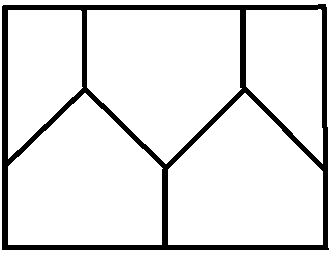
Divide the given region in four congruent pieces.

The figure is obtained by joining three squares.
Pieces are congruent if one can be obtained from the other using translations, rotations, and reflections (in other words, they have the same shape and same area).
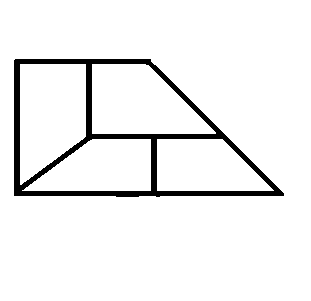
Divide the given region in four congruent pieces.
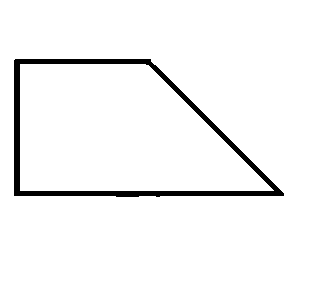
The given figure is a trapezoid obtained by gluing together a square and an isosceles right triangle.
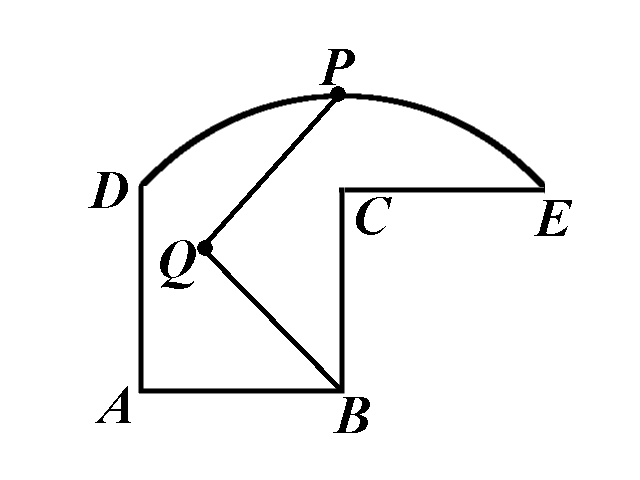
In the figure below, \(ABCD\) is a square, \(CE=BC\), and the arc \(DE\) is centered at \(B\).
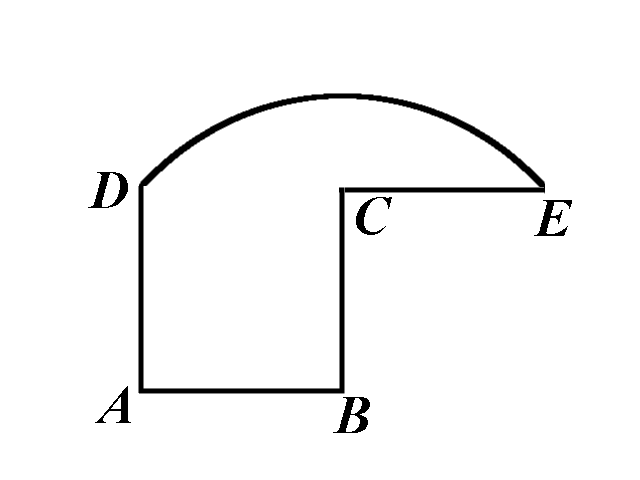
Divide the given region in two congruent pieces using a curve that has only two common points with the given figure.
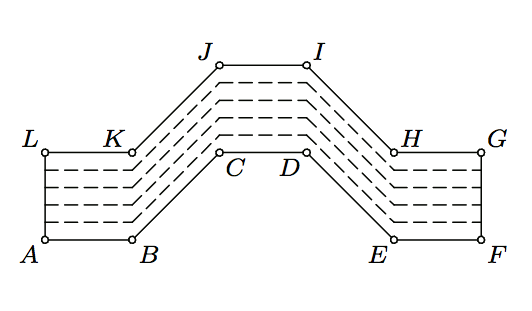
Divide the given region in five congruent pieces.
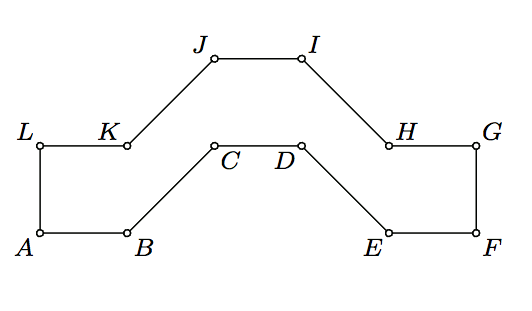
In the figure above \(ABKL\), \(CDIJ\), and \(EFGH\) are congruent squares and \(KBCJ\), \(DEHI\) are parallelograms with \(KB=BC=DE=EH\).
Given three squares of dimensions \(2\times 2\), \(3\times 3\), and \(6\times 6\), choose two of them and cut into two pieces each such that from the obtained \(5\) figures it is possible to assemble another square.
Does there exist a convex polygon that can be partitioned into non-convex quadrilaterals?
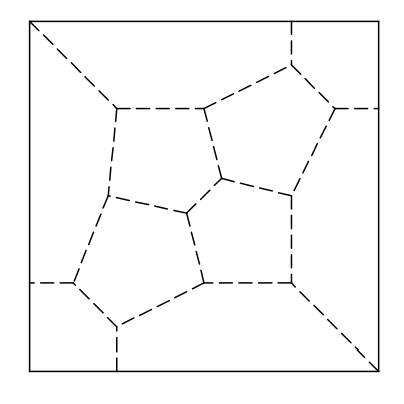
Is it possible to divide a square into \(10\) convex pentagons?
Remark. A polygon is convex if all its internal angles are less than \(180^{\circ}\).
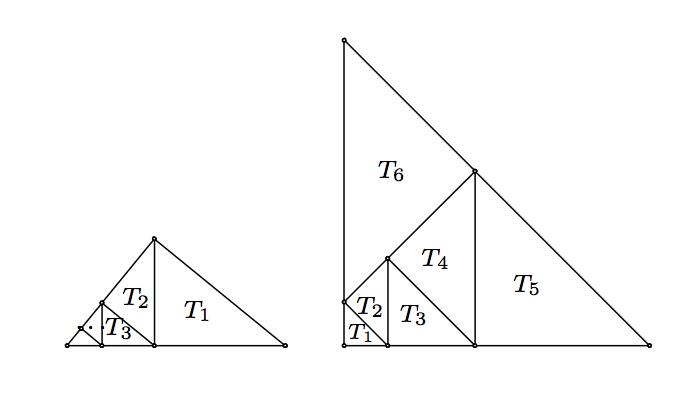
Let \(\triangle ABC\) be a triangle such that \(\angle A=90^{\circ}\). Determine whether it is possible to partition \(\triangle ABC\) into 2012 smaller triangles in such a way that the following two conditions are satisfied
- (i) Each triangle in the partition is similar to \(\triangle ABC\);
- (ii) No two triangles in the partition have the same area.
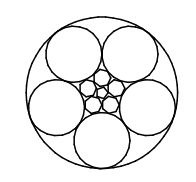
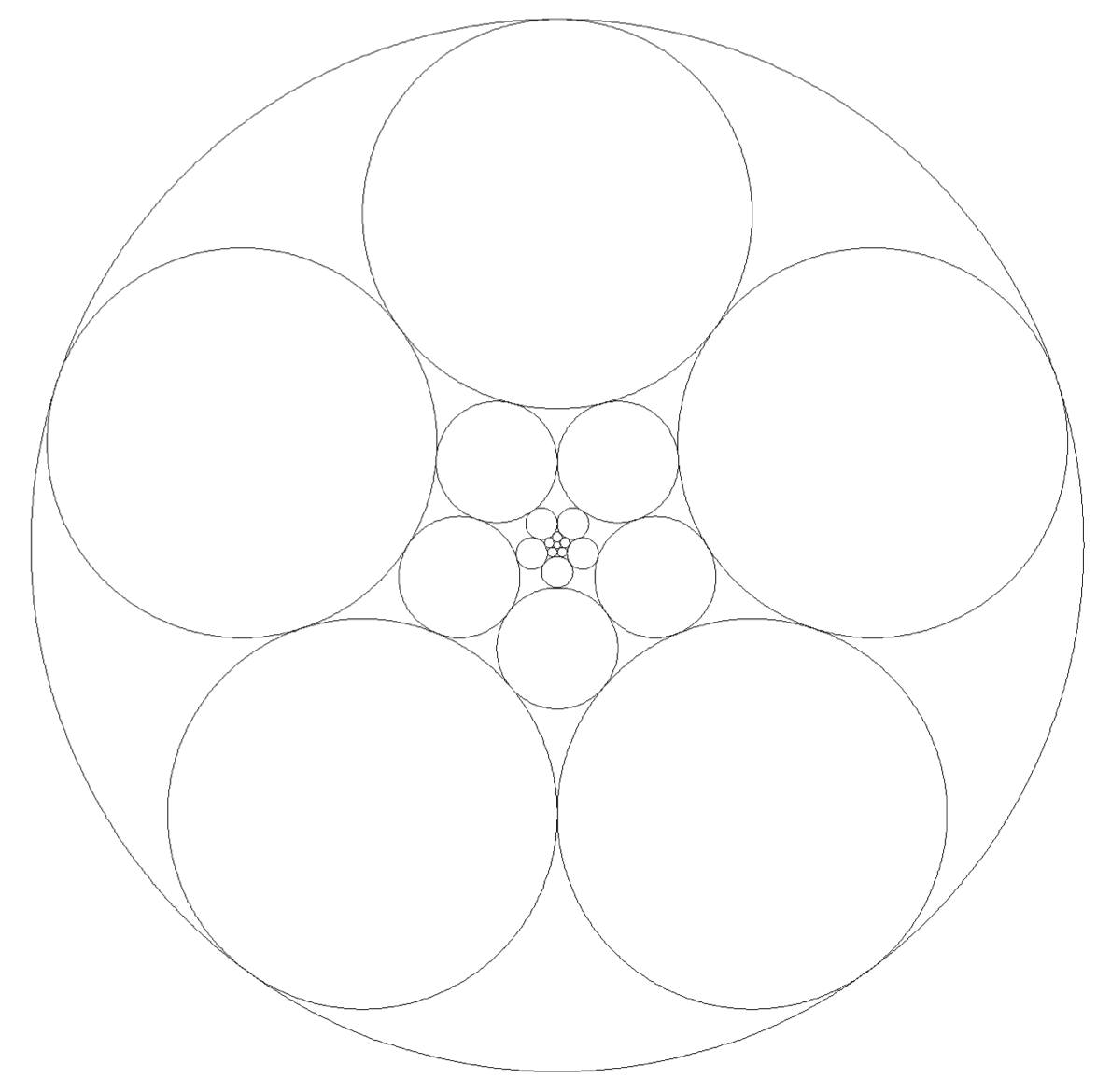
A finite set of circles in the plane is called nice if it satisfies the following three conditions:
- (i) No two circles intersect in more than one point;
- (ii) For every point \(A\) of the plane there are at most two circles passing through \(A\);
- (iii) Each circle from the set is tangent to exactly \(5\) other circles form the set.
Does there exist a nice set consisting of exactly
- (a) 2011 circles?
- (b) 2012 circles?
A finite set of unit circles is given in a plane such that the area of their union \(U\) is \(S\). Prove that there exists a subset of mutually disjoint circles such that the area of their union is greater than \(\frac{2S}9\).
(Vladimir Jankovic, IMO Shortlist 1981)