| 1. | Sets |
| 2. | Functions |
| 3. | Introduction to counting |
| 4. | Counting with bijections |
| 5. | Generating functions |
| 6. | Theory of generating functions (Milan Novaković) |
| 7. | Burnside's lemma |
| 8. | Polya's theorem |
Burnside's Lemma
Burnside’s lemma helps us solve the following problem:
Find the number of distinct cubes that can be made by painting each face of a given cube in one of the 5 given colors (not all of the colors have to be used). Cubes are distinct if they cannot be obtained from each other using rotations.
We will find this number by doing an extensive study of what makes two paintings the same. And before we can start doing that we need to make a mathematically precise notion for "painting of a cube."
Paintings of cubes
Let us denote our five colors by \(R\), \(G\), \(B\), \(Y\), and \(W\) (the letters stand for red, green, blue, yellow, and white). We will denote by \(C\) the set of all colors, i.e. \[C=\left\{R, G, B, Y, W\right\}.\]
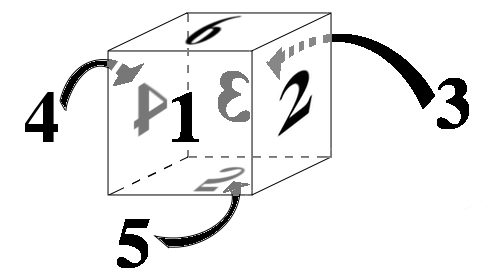
Let us fix one un-painted cube and label its faces with numbers 1, 2, 3, 4, 5, 6 as shown in the picture. The side 1 is facing us, 2 is to the left, 3 is in the back, 4 is to the right. The bottom face is 5 and the top is 6.
We will talk about colorings of this fixed cube.

Consider the cube from the picture above. The front face (face 1, as we decided to call it) is red but it is punctured so you can see inside the cube. Face 1 is red, 2 is blue, 3 is green, 4 is yellow, 5 is blue, and 6 is green. Each painting of a cube in 5 colors can be represented as a sequence of 6 elements. The elements of each sequence are the letters \(R\), \(G\), \(B\), \(Y\), and \(W\). The cube in our example will correspond to the sequence (\(R,B,G,Y,B,G\)). The set \(U\) of all paintings can be written as \[U=C^6.\]
The number of elements of \(U\) is \(5^6\) but that is not the number we are after. For example the paintings (\(R, B, B, B, B, B\)) and (\(B, R, B, B, B, B\)) can be obtained from each other using rotations. This is the reason why we define an equivalence relation among the paintings.
An equivalence relation on the set \(U\)
We will define a relation \(\sim\) on the set \(U\) of all colorings. We say that two colorings \((x_1,x_2,\) ..., \(x_6)\) and \((y_1,y_2,\) ..., \(y_6)\) are in relation \(\sim\) if they represent colorings of two cubes that can be obtained from one another using rotations. We write \[(x_1, x_2, \dots, x_6)\sim (y_1, y_2, \dots, y_6).\]
For example, we have: \[(R,B,G,Y,B,G)\sim (B, G, Y, R, B, G)\sim (G, Y, R, B, B, G)\sim (B,G,G,R,Y,B).\]
This relation \(\sim\) is an equivalence relation. It is determined by the action of the rotation group of cube on the set \(S\). The following section will further clarify this.
Permutation group of cube
Consider the cube whose faces are labeled by 1, 2, 3, 4, 5, 6 as before. Rotations of the cube induce permutations on the set {1,2,3,4,5,6}. For example, the rotation for \(90^{\circ}\) around the line connecting the centers of faces 5 and 6 induces the permutation \[\rho=\left(\begin{array}{cccccc} 1&2&3&4&5&6 \newline 2& 3& 4& 1& 5& 6\end{array}\right)\] The previous notation means that the face 1 is mapped to 2; 2 is mapped to 3; 3 to 4; 4 to 1; 5 goes to 5 (it is fixed under this rotation); and 6 goes to 6. We can also write \(\rho(1)=2\), \(\rho(2)=3\), \(\rho(3)=4\), etc.
Let us illustrate one rotation of the cube. We will first define the axis by defining two points \(X\) and \(Y\). Let \(X\) be the common vertex of thefaces \(1\), \(2\), and \(5\)t. Let \(Y\) be the common vertex of the faces \(3\), \(4\), and \(6\). The following animation shows the rotation of the cube with the axis \(XY\).
The following 24 permutations correspond to rotations of the cube:
\[ e=\left(\begin{array}{cccccc} 1&2&3&4&5&6 \newline 1& 2& 3& 4& 5& 6\end{array}\right)\;\;\; \rho_1=\left(\begin{array}{cccccc} 1&2&3&4&5&6 \newline 2& 3& 4& 1& 5& 6\end{array}\right)\;\;\; \rho_2=\left(\begin{array}{cccccc} 1&2&3&4&5&6 \newline 3& 4& 1& 2& 5& 6\end{array}\right)\] \[\rho_3=\left(\begin{array}{cccccc} 1&2&3&4&5&6 \newline 4& 1& 2& 3& 5& 6\end{array}\right)\;\;\; \rho_4=\left(\begin{array}{cccccc} 1&2&3&4&5&6 \newline 6& 2&5& 4& 1&3 \end{array}\right)\;\;\; \rho_5=\left(\begin{array}{cccccc} 1&2&3&4&5&6 \newline 3& 2&1& 4& 6&5 \end{array}\right)\] \[ \rho_6=\left(\begin{array}{cccccc} 1&2&3&4&5&6 \newline 5& 2&6& 4& 3&1 \end{array}\right)\;\;\; \rho_7=\left(\begin{array}{cccccc} 1&2&3&4&5&6 \newline 1& 6&3& 5&2&4 \end{array}\right)\;\;\; \rho_8=\left(\begin{array}{cccccc} 1&2&3&4&5&6 \newline 1& 4&3& 2&6&5 \end{array}\right)\] \[\rho_9=\left(\begin{array}{cccccc} 1&2&3&4&5&6\newline 1& 5&3& 6&4&2 \end{array}\right)\;\;\; \rho_{10}=\left(\begin{array}{cccccc} 1&2&3&4&5&6 \newline 5& 3&6& 1&4&2 \end{array}\right)\;\;\; \rho_{11}=\left(\begin{array}{cccccc} 1&2&3&4&5&6 \newline 4& 6&2& 5&1&3 \end{array}\right)\] \[ \rho_{12}=\left(\begin{array}{cccccc} 1&2&3&4&5& 6 \newline 2&5&4&6&1&3 \end{array}\right)\;\;\; \rho_{13}=\left(\begin{array}{cccccc} 1&2&3&4&5&6 \newline 5&1&6&3&2&4 \end{array}\right)\;\;\; \rho_{14}=\left(\begin{array}{cccccc} 1&2&3&4&5&6 \newline 6&3&5&1&2&4 \end{array}\right)\] \[ \rho_{15}=\left(\begin{array}{cccccc} 1&2&3&4&5&6 \newline 4&5&2&6&3&1 \end{array}\right)\;\;\; \rho_{16}=\left(\begin{array}{cccccc} 1&2&3&4&5&6 \newline 2&6&4&5&3&1 \end{array}\right)\;\;\; \rho_{17}=\left(\begin{array}{cccccc} 1&2&3&4&5&6 \newline 6&1&5&3&4&2 \end{array}\right)\] \[ \rho_{18}=\left(\begin{array}{cccccc} 1&2&3&4&5&6 \newline 5&4&6&2&1&3 \end{array}\right)\;\;\; \rho_{19}=\left(\begin{array}{cccccc} 1&2&3&4&5&6 \newline 3&5&1&6&2&4 \end{array}\right)\;\;\; \rho_{20}=\left(\begin{array}{cccccc} 1&2&3&4&5&6 \newline 6&4&5&2&3&1 \end{array}\right)\] \[\rho_{21}=\left(\begin{array}{cccccc} 1&2&3&4&5&6 \newline 3&6&1&5&4&2 \end{array}\right)\;\;\; \rho_{22}=\left(\begin{array}{cccccc} 1&2&3&4&5&6 \newline 4&3&2&1&6&5 \end{array}\right)\;\;\; \rho_{23}=\left(\begin{array}{cccccc} 1&2&3&4&5&6 \newline 2&1&4&3&6&5 \end{array}\right)\]Composition of permutations
Since permutations are functions, we can talk about their composition. For two permutations \(\rho\) and \(\sigma \) we will define their composition as a function \(\rho\circ\sigma: \{1,2,3,4,5,6\}\to\{1,2,3,4,5,6\}\). The precise definition is \(\rho\circ\sigma(i)=\rho(\sigma(i))\) for each \(i\in\{1,2,\dots, 6\}\).
To give an example we recall the previously defined permutation \(\rho\), and we define another permutation \(\sigma\) in the following way:
\[\sigma=\left(\begin{array}{cccccc} 1&2&3&4&5&6 \newline 5& 2& 6& 4& 3& 1\end{array}\right).\]Then we have \(\rho(\sigma(1))=\rho(5)=5\), \(\rho(\sigma(2))=\rho(2)=3\), \(\rho(\sigma(3))=\rho(6)=6\), \(\rho(\sigma(4))=\rho(4)=1\), \(\rho(\sigma(5))=\rho(3)=4\), and \(\rho(\sigma(6))=\rho(1)=2\), hence
\[\rho\circ\sigma= \left(\begin{array}{cccccc} 1&2&3&4&5&6 \newline 5& 3& 6& 1& 4& 2\end{array}\right).\]Cycles
Cycles are the simplest possible permutations. For example, the above defined permutation \(\rho\) is a cycle because it sends \(1\mapsto 2\), \(2\mapsto 3\), \(3\mapsto 4\), \(4\mapsto 1\) and keeps the remaining numbers fixed. Similarly, the permutation \(\sigma\) is a cycle because \(1\mapsto 5\mapsto 3\mapsto 6\mapsto 1\). We also write \(\rho=(1234)\) and \(\sigma=(1536)\).Decomposition into cycles
Each permutation can be decomposed into cycles. The given permutation \(\rho\) can be written as \(\rho=(1234)(5)(6)\), while \(\rho\circ\sigma=(154)(236)\).Group of permutations of the cube in cyclic representation
We can now put those 24 rotations of the cube in cyclic representation:This permutation group acts on the set \(U\) of all colorings in the following way: Each permutation, can be applied to a coloring and produce another coloring.
The set \(G=\{e, \rho_1,\dots, \rho_{23}\}\) forms a group with respect to composition of permutations. For each coloring \(s\in S\), consider the set \[G_s=\{g\in G: g(s)=s\}.\] The set \(G_s\) is called the stabilizer of \(s\), and denotes all the permutation that leave \(s\) invariant.
For each permutation \(g\in G\), denote by Inv(\(g\)) the set of all elements of \(S\) that are immune to \(g\). In correct mathematical language, we write
\[\mbox{Inv }(g)=\{s\in S: g(s)=s\}.\]\[|E(s)|\cdot |G_s|=|G|.\]
\[|E|=\frac1{|G|}\sum_{g\in G} \mbox{Inv }(g).\]
Solution to Example 1.
Consider the set \(S\) of all possible colorings. As indicated above, we write \(s\sim t\) if there is a permutation \(g\in G\) such that \(g(s)=t\). This \(\sim\) is an equivalence relation on \(S\) and equivalence classes are precisely the colorings of the cube that can’t be obtained using rotations from one another. Burnside’s lemma provides a way to calculate the number of equivalence classes. Denote by \(E\) the set of all equivalence classes. We have
\[|E|=\frac1{|G|}\sum_{g\in G} |\mbox{Inv }(g)|=\frac{1}{24}\cdot \sum_{g\in G} |\mbox{Inv }(g)|.\]
We now need to evaluate |Inv(\(e\))|, |Inv(\(\rho_1\))|, |Inv(\(\rho_2\))|, ..., |Inv(\(\rho_{23}\))| and to add these numbers.
\(1^{\circ}\) The set Inv(\(e\)) consists of all colorings that are not changed by \(e\). These are all colorings, hence |Inv(\(e\))|=\(5^6\).
\(2^{\circ}\) Let us consider now the set Inv(\(\rho_1\)). A coloring \(s\) = \((s_1, s_2, \cdots, s_6)\) belongs to this set if it is immune to \(\rho_1\). This will happen if and only if \(s_1=s_2=s_3=s_4\). The number of such coloring is \(5^3\) (because for the faces 1, 2, 3, 4 we have to use the same color, which can be chosen in 5 ways. For each choice of that color there are 5 choices for the face 5, and for each coloring of 1, 2, 3, 4, 5 there are 5 choices for the coloring of the face 6).
Similarly, we get that \(|\mbox{Inv }(\rho_3)|=|\mbox{Inv }(\rho_4)|=|\mbox{Inv }(\rho_6)|=|\mbox{Inv }(\rho_7)|=|\mbox{Inv }(\rho_9)|=5^3\). Thus
\[|\mbox{Inv }(\rho_1)|+|\mbox{Inv }(\rho_3)|+|\mbox{Inv }(\rho_4)|+|\mbox{Inv }(\rho_6)|+|\mbox{Inv }(\rho_7)|+|\mbox{Inv }(\rho_9)|=6\cdot 5^3.\]
\(3^{\circ}\) Since each of \(\rho_2\), \(\rho_5\), \(\rho_8\) consists of 4 cycles we get |Inv(\(\rho_2\))|= |Inv(\(\rho_5\))|= |Inv(\(\rho_8\))|=\(5^4\) and
\[|\mbox{Inv }(\rho_2)|+|\mbox{Inv }(\rho_5)|+|\mbox{Inv }(\rho_8)|=3\cdot 5^4.\]
\(4^{\circ}\) Similarly to the previous reasoning we get
\[|\mbox{Inv }(\rho_{10})|+|\mbox{Inv }(\rho_{11})|+\cdots +|\mbox{Inv }(\rho_{17})|=8\cdot 5^2,\;\;\mbox{ and }\]
\(5^{\circ}\)
\[|\mbox{Inv }(\rho_{18})|+|\mbox{Inv }(\rho_{19})|+\cdots+|\mbox{Inv }(\rho_{23})|=6\cdot 5^3.\]
Therefore \[|E|=\frac1{24}\cdot \left(5^6+12\cdot 5^3+3\cdot 5^4+8\cdot 5^2\right).\]