Case 2.2.2.2: Calculation of \(P_{2.2.2.2^{\circ}}(k)\)
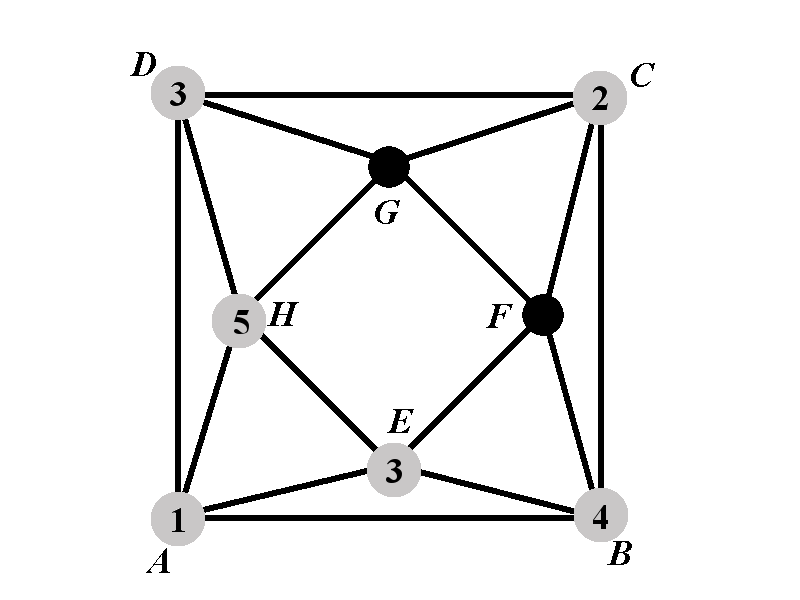
The vertex \(G\) cannot have any of the colors \(2\), \(3\), \(5\). We will consider two cases: Case 2.2.2.2.1 in which the vertex \(G\) has the color \(4\) and case 2.2.2.2.2 in which the vertex \(G\) has none of the colors from \(\{2,3,4,5\}\).
Let us denote by \(P_{2.2.2.2.1^{\circ}}(k)\) the number of proper colorings of \(\Gamma\) in which the vertices \(A\), \(B\), \(C\), \(D\), \(E\), \(G\), and \(H\) have the colors \(1\), \(4\), \(2\), \(3\), \(3\), \(4\), and \(5\), respectively. Let us denote by \(P_{2.2.2.2.2^{\circ}}(k)\) the number of proper colorings of \(\Gamma\) in which the vertices \(A\), \(B\), \(C\), \(D\), \(E\), \(G\), and \(H\) have the colors \(1\), \(4\), \(2\), \(3\), \(3\), \(1\), and \(5\), respectively.
The quantity \(P_{2.2.2.2^{\circ}}(k)\) satisfies \[P_{2.2.2.2^{\circ}}(k)=P_{2.2.2.2.1^{\circ}}(k)+(k-4)P_{2.2.2.2.2^{\circ}}(k).\]
Case 2.2.2.2.1: Calculation of \(P_{2.2.2.2.1^{\circ}}(k)\)
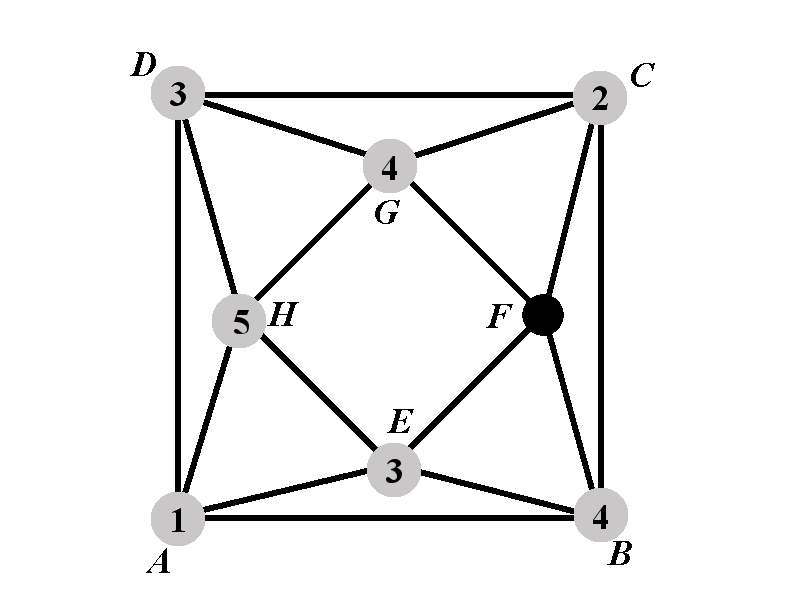
It remains to find the number of colorings for the vertex \(F\). The vertex \(F\) cannot have any of the colors \(2\), \(3\), \(4\). Hence there are \(k-3\) available colors for \(F\) and \[P_{2.2.2.2.1^{\circ}}(k)=k-3.\]
Case 2.2.2.2.2: Calculation of \(P_{2.2.2.2.2^{\circ}}(k)\)
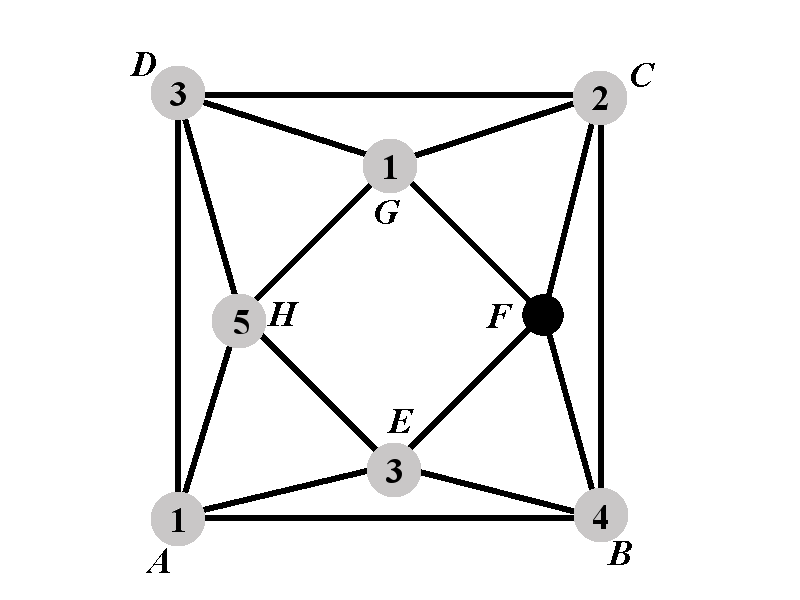
The vertex \(F\) cannot have any of the colors \(1\), \(2\), \(3\), \(4\). Hence there are \(k-4\) available colors for \(F\) and \[P_{2.2.2.2.2^{\circ}}(k)=k-4.\]
Therefore \begin{eqnarray*}P_{2.2.2.2^{\circ}}(k)&=&P_{2.2.2.2.1^{\circ}}(k)+(k-4)P_{2.2.2.2.2^{\circ}}(k)\newline &=&k-3+(k-4)\cdot (k-4)=k-3+(k-4)^2. \end{eqnarray*}