Case 2.1: Calculation of \(P_{2.1^{\circ}}(k)\)
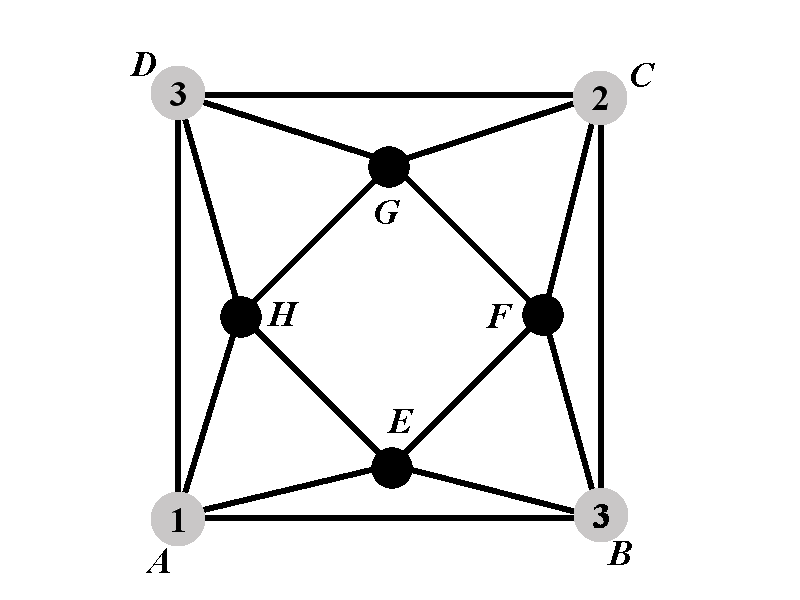
Observe that none of the vertices \(E\) and \(H\) can have color \(1\) or color \(3\). We will consider two sub-cases: Sub-case 2.1.1 is when one of the vertices \(E\) and \(H\) has the color \(2\). The sub-case 2.1.1 is when none of \(E\) and \(H\) has a color from \(\{1,2,3\}\).
In the case 2.1.1 the number of colorings in which \(E\) has the color \(2\) is equal to the number of colorings in which \(H\) has the color \(2\). If the vertex \(E\) has the color \(2\) then there are \(k-3\) choices for the color of \(H\). Let us denote by \(P_{2.1.1^{\circ}}(k)\) the number of proper colorings of \(\Gamma\) in which \(A\), \(B\), \(C\), \(D\), \(E\), and \(H\) have the colors \(1\), \(3\), \(2\), \(3\), \(2\), and \(4\). The total number of colorings in the case 2.1.1 is \(2\cdot (k-3)\cdot P_{2.1.1^{\circ}}(k)\).
In the case 2.1.2 the vertices \(E\) and \(H\) cannot have any of the colors from \(\{1,2,3\}\). In addition, the vertices \(E\) and \(H\) must be of mutually different colors. There are \(k-3\) choices for the color of \(E\) and for each of those choices there are \(k-4\) available colors for \(H\). Let us denote by \(P_{2.1.2^{\circ}}(k)\) the number of proper colorings of \(\Gamma\) in which \(A\), \(B\), \(C\), \(D\), \(E\), and \(H\) have the colors \(1\), \(3\), \(2\), \(3\), \(4\), and \(5\), respectively. The total number of colorings in the case 2.1.2 is \((k-3)(k-4)P_{2.1.2^{\circ}}(k)\).
Therefore the polynomial \(P_{2.1^{\circ}}(k)\) satisfies \[P_{2.1^{\circ}}=2(k-3)P_{2.1.1^{\circ}}(k)+(k-3)(k-4)P_{2.1.2^{\circ}}(k).\]
Case 2.1.1: Calculation of \(P_{2.1.1^{\circ}}(k)\)
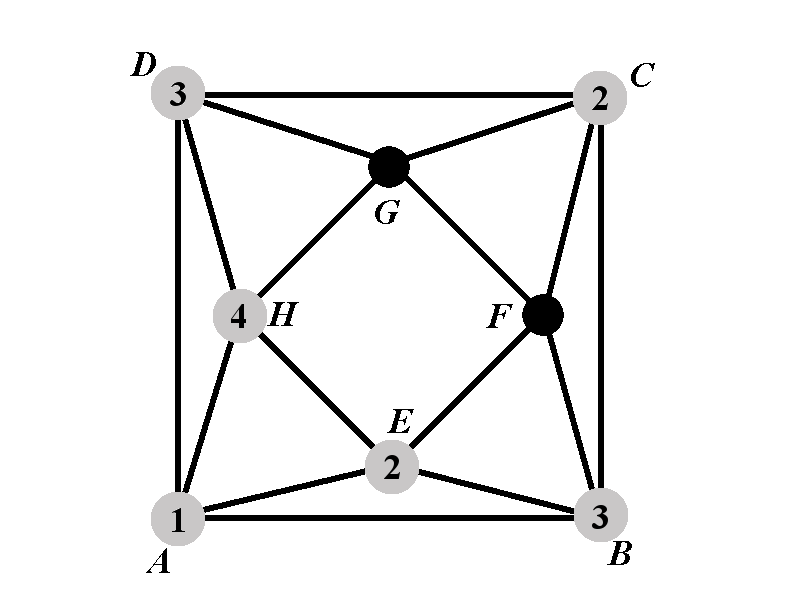
The vertex \(G\) cannot have any of the colors \(2\), \(3\), and \(4\). There are \(k-3\) colors available for \(G\). For any of those \(k-3\) choices there are exactly \(k-3\) colors available for \(F\) (the color \(4\) is back as an option for \(F\), but the color that \(G\) took is out). Therefore \[P_{2.1.1^{\circ}}(k)=(k-3)^2.\]
Case 2.1.2: Calculation of \(P_{2.1.2^{\circ}}(k)\)
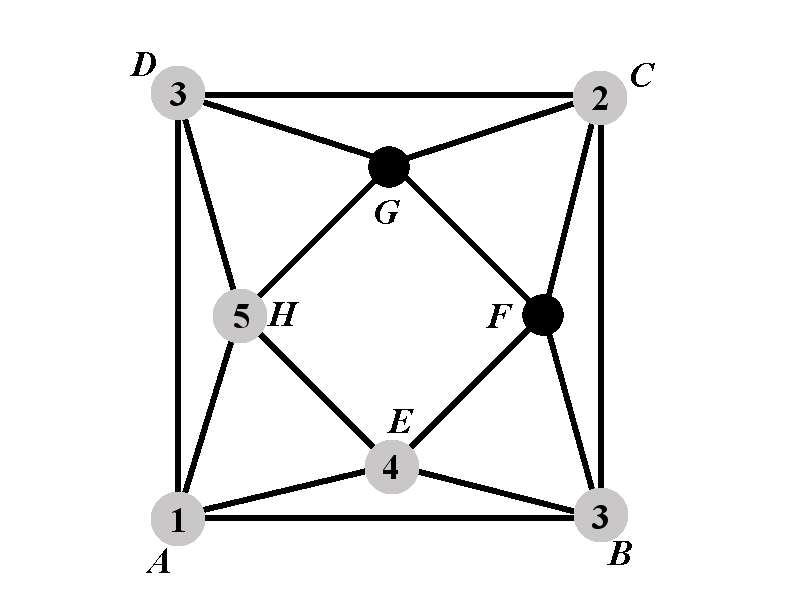
The case 2.1.2 further brakes into two sub-cases. Let us observe the vertex \(F\). The vertex \(F\) cannot have any of the colors from the set \(\{2,3,4\}\). We will consider the sub-case 2.1.2.1 in which the vertex \(F\) has the color 5, and the sub-case 2.1.2.2 in which the vertex \(F\) has a color outside of the set \(\{2,3,4,5\}\). In the sub-case 2.1.2.2 there are \(k-4\) possibilities for \(F\).
Denote by \(P_{2.1.2.1^{\circ}}(k)\) the number of proper colorings of \(\Gamma\) such that the vertices \(A\), \(B\), \(C\), \(D\), \(E\), \(F\), and \(H\) have the colors \(1\), \(3\), \(2\), \(3\), \(4\), \(5\), and \(5\), respectively. Denote by \(P_{2.1.2.2^{\circ}}(k)\) the number of proper colorings of \(\Gamma\) such that the vertices \(A\), \(B\), \(C\), \(D\), \(E\), \(F\), and \(H\) have the colors \(1\), \(3\), \(2\), \(3\), \(4\), \(1\), and \(5\), respectively.
The number \(P_{2.1.2^{\circ}}(k)\) satisfies \[P_{2.1.2^{\circ}}(k)=P_{2.1.2.1^{\circ}}(k)+(k-4)P_{2.1.2.2^{\circ}}(k).\]
Case 2.1.2.1: Calculation of \(P_{2.1.2.1^{\circ}}(k)\)

It remains to count the number of ways to color the vertex \(G\) that would complete the proper coloring of \(\Gamma\). The vertex \(G\) cannot have any of the colors from the set \(\{2,3,5\}\). Therefore there are \(k-3\) available colors for \(G\). Hence \[P_{2.1.2.1^{\circ}}(k)=k-3.\]
Case 2.1.2.2: Calculation of \(P_{2.1.2.2^{\circ}}(k)\)
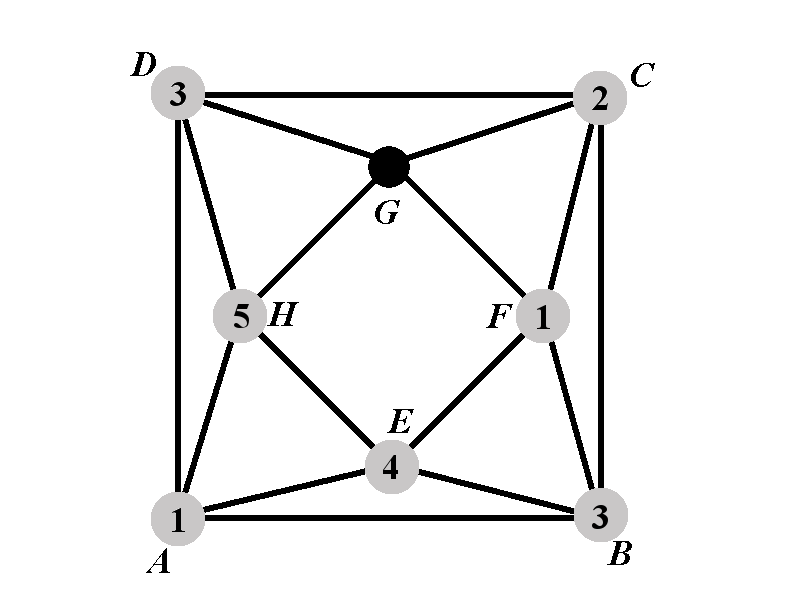
The vertex \(G\) cannot have any of the colors from the set \(\{1,2,3,5\}\). Therefore there are \(k-4\) available colors for \(G\) and \[P_{2.1.2.2^{\circ}}(k)=k-4.\]
Final Calculation of \(P_{2.1^{\circ}}(k)\)
We now have all the ingredients to complete the calculation of \(P_{2.1^{\circ}}(k)\). \begin{eqnarray*}P_{2.1^{\circ}}(k)&=&2(k-3)P_{2.1.1^{\circ}}(k)+(k-3)(k-4)P_{2.1.2^{\circ}}(k)\newline &=&2(k-3)\cdot (k-3)^2+(k-3)(k-4)\left(P_{2.1.2.1^{\circ}}(k)+(k-4)P_{2.1.2.2^{\circ}}(k)\right)\newline &=&2(k-3)^3+(k-3)(k-4)\left(k-3+(k-4)\cdot(k-4)\right)\newline &=&(k-3)\left[2(k-3)^2+(k-3)(k-4)+(k-4)^3\right]\newline &=&(k-3)\left(k^3-9k^2+29k-34\right). \end{eqnarray*}