Convex Functions
To prove some of the fundamental results we will need to
use convexity of certain functions. Proofs of the theorems
of Young, Minkowski, and Holder will require us to use
very basic facts -- you should be fine if you just read the
definition of convexity and the example in which some famous convex functions are listed. However,
the section on Karamata’s inequality will require some
deeper knowledge which you can find here.
Definition (Convexity)
The function \(f:[a,b]
\rightarrow \mathbb R\) is convex if for any \(x_1,x_2\in[a,b]\) and
any \(\lambda \in (0,1)\) the following inequality holds:
\begin{eqnarray*}
f(\lambda x_1+(1-\lambda)x_2)\leq \lambda f(x_1)+(1-\lambda)f(x_2).
\quad\quad\quad\quad\quad (1)
\end{eqnarray*}
Function is called concave if \(-f\) is convex.
If the inequality
in (1) is strict then the function is called
strictly convex.
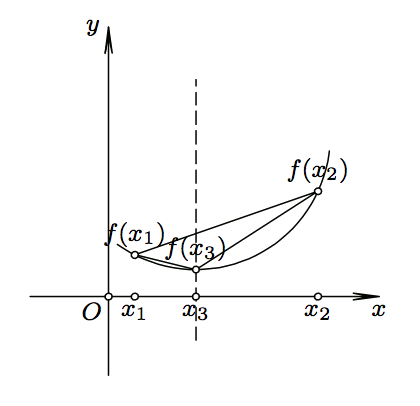
Now we will give a geometrical interpretation of
convexity. Take any \(x_3\in(x_1,x_2)\).
There is \(\lambda\in(0,1)\) such that
\(x_3=\lambda x_1+(1-\lambda) x_2\). Let’s paint in
green the
line passing through \(x_3\) and
parallel to the \(y\) axis.
Let’s paint in red the chord connecting the points
\((x_1,f(x_1))\) and \((x_2, f(x_2))\). Assume that the green
line and the red chord intersect at the yellow point.
The \(y\) coordinate
(also called the height)
of the yellow point
is:
\[\lambda f(x_1)+(1-\lambda)f(x_2).\]
The inequality (1) means exactly that the
the green line intersects the graph of a
function below the red chord. If \(f\)
is strictly convex then the equality can hold in (1)
if and only if \(x_1=x_2\).
ExampleThe following functions are
convex: \(e^x\), \(x^p\) (for \(p\geq 1\), \(x > 0\)),
\(\frac1x\) (\(x\neq 0\)),
while the functions \(\log x\) (\(x > 0\)), \(\sin x\) (\(0\leq x\leq \pi\)) ,
\(\cos x\) (\(-\pi/2\leq x\leq \pi/2\)) are concave.
All functions mentioned in the previous example are elementary
functions, and proving the convexity/concavity for them would
require us to go to the very basics of their foundation, and
we will not do that. In many of the examples and problems
respective functions are slight modifications of elementary
functions. Their convexity (or concavity) is something we
don’t have to verify.
However, we will develop some criteria
for verifying the convexity of more complex combinations
of functions.
Let us take another
look at our picture above and compare the slopes
of the three drawn lines. The line connecting \((x_1, f(x_1))\)
with \((x_3, f(x_3))\) has the smallest slope, while the line
connecting \((x_3, f(x_3))\) with \((x_2, f(x_2))\) has the
largest slope. In the following theorem we will state and
prove that the convex function has always an increasing slope.
Theorem 1. Let \(f:[a,b]\rightarrow \mathbb R\) be a
convex function and \(a\leq x_1 < x_3 < x_2\leq b\). Then
\begin{eqnarray}
\frac{f(x_3)-f(x_1)}{x_3-x_1}\leq
\frac{f(x_2)-f(x_1)}{x_2-x_1} \leq \frac{f(x_2)-f(x_3)}
{x_2-x_3}. \quad\quad\quad\quad\quad (2)
\end{eqnarray}
We can write \(x_3=\lambda x_1+(1-\lambda)x_2\)
for some \(\lambda\in(0,1)\). More precisely
\(\lambda=\frac{x_2-x_3}{x_2-x_1}\), and
\(1-\lambda=\frac{x_3-x_1}{x_2-x_1}\). From (0) we
get
\begin{eqnarray*}
f(x_3)\leq \frac{x_2-x_3}{x_2-x_1}f(x_1)+\frac{x_3-x_1}
{x_2-x_1}f(x_2).\end{eqnarray*} Subtracting \(f(x_1)\) from both
sides of the last inequality
yields \(f(x_3)-f(x_1)=
-\frac{x_3-x_1}{x_2-x_1}f(x_1)+\frac{x_3-x_1}
{x_2-x_1}f(x_2)\) giving immediately the first inequality of
(2). The second inequality of (2)
is obtained in an analogous way.
The rest of this chapter is using some of the properties of
limits, continuity and differentiability. If you are not
familiar with basic calculus, you may skip that part, and
you will be able to understand most of what follows. Theorem
3 is a tool for verifying
the convexity for differentiable functions that we mentioned
before. The theorem 3 will
be used it in the proof of Karamata’s inequality.
Theorem 2 If \(f: (a,b)\rightarrow
\mathbb R\) is a convex function, then \(f\) is continuous and
at every point \(x\in(a,b)\) it has both left and right
derivative \(f^{\prime}_-(x)\) and \(f^{\prime}_+(x)\). Both \(f^{\prime}_-\) and \(f^{\prime}_+\)
are increasing functions on \((a,b)\) and \(f^{\prime}_-(x)\leq f^{\prime}_+(x)\).
Theorem 1 implies that for fixed \(x\) the
function
\(\varphi(t)=\frac{f(t)-f(x)}{t-x}\), \(t\neq x\) is an increasing function
bounded both by below and above. More precisely, if
\(t_0\) and \(t_1\) are any two numbers from \((a,b)\) such that
\(t_0 < x < t_1\) we have: \[\frac{f(x)-f(t_0)}{x-t_0}\leq
\varphi(t)\leq \frac{f(t_1)-f(x)}{t_1-x}.\]
This specially means that there are \(\lim_{t\rightarrow x-}
\varphi(t)\) and \(\lim_{t\rightarrow x+} \varphi(t)\). The first one
is precisely the left, and the second one -- the right
derivative of
\(\varphi\) at \(x\). Since the existence of both left and right
derivatives implies the continuity, the statement is proved.
Theorem 3
If \(f: (a,b)\rightarrow \mathbb R\) is a twice
differentiable function. Then \(f\) is convex on \((a,b)\)
if and
only if \(f^{\prime\prime}(x)\geq 0\) for every
\(x\in(a,b)\). Moreover, if \(f^{\prime\prime}(x) > 0\) then \(f\) is strictly
convex.
This theorem is the immediate consequence of
the previous one.
