| 1. | Introduction |
| 2. | Geometric substitution |
| 3. | Important results in geometry |
| 4. | Inequalities in triangle geometry |
| 5. | Erdos-Mordell Inequality |
| 6. | Brunn-Minkowski inequality |
| 7. | Problems |
Important Results in Geometry
In the sequel, we will write \(BM\) as the length of the vector \(\overrightarrow{BM}\). The result of the previous theorem can be also expressed as \[\overrightarrow{AM}=\frac{{MC}}{ {BC}}\cdot \overrightarrow {AB}+\frac{ {BM}}{ {BC}}\cdot \overrightarrow {AC}.\]
Let \(ABC\) be a triangle whose side lengths are \(AB=c\), \(BC=a\), \(CA=b\). Denote by \(A^{\prime\prime}\) the point where the internal bisector intersects the side \(BC\). Let \(p\) be the semi-perimeter of the triangle \(ABC\).
- (a) Prove that \(BA^{\prime\prime}:A^{\prime\prime}C=AB:AC\).
- (b) Prove that \(l_a=AA^{\prime\prime}=\frac{2}{b+c}\cdot \sqrt{bcp(p-a)}\).
Let \(O\) be the circumcenter of the triangle \(ABC\) and \(G\) its centroid. Prove that \(OG^2=R^2-\frac19(a^2+b^2+c^2)\).
If \(a\), \(b\), \(c\) are the lengths of the sides of \(\triangle ABC\) and \(R\) its circumradius prove that \[9R^2\geq a^2+b^2+c^2.\]
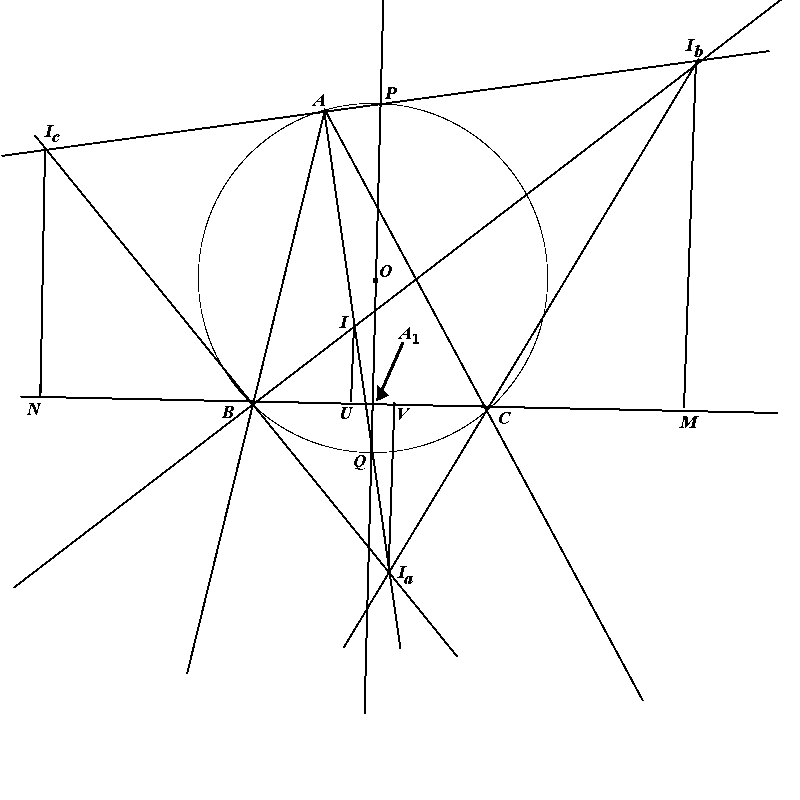
Let \(ABC\) be the given triangle and let \(O\) be its circumcenter, \(I\) its incenter, \(I_a\), \(I_b\), \(I_c\) the centers of the excircles \(k_a\), \(k_b\), \(k_c\) (corresponding to the sides \(BC\), \(CA\), \(AB\)), and \(G\) its centroid. Denote by \(a\), \(b\), \(c\) the side lengths, \(R\) the circumradius, and by \(r\) the inradius or \(\triangle ABC\). Denote by\(r_a\), \(r_b\), \(r_c\) be the exradii. Let \(p\) be the semi-perimeter of \(\triangle ABC\). Then the following statements hold:
- (a) \(AI\) intersects the circumcircle at the midpoint \(Q\) of the arc \(BC\). \(I_bI_c\) contains the point \(A\) and the midpoint \(P\) of the arc \(BC\) that contains \(A\). The point \(O\) belongs to \(PQ\).
- (b) If \(M\) and \(N\) are the points of tangency of \(k_b\) and \(k_c\) with \(BC\), then \(P\) is the midpoint of \(I_aI_b\), \(A_1\) is the midpoint of \(MN\) and \(PA_1=\frac{r_b+r_c}2\).
- (c) Denote by \(U\) the point of tangency of the incircle with \(BC\) and by \(V\) the point of tangency of \(k_a\) with \(BC\). Then \(A_1\) is the midpoint of \(UV\), \(Q\) is the midpoint of \(II_a\), and \(QA_1=\frac{r_a-r}2\).
- (d) (Heron’s formula) \(S_{ABC}=\sqrt{p(p-a)(p-b)(p-c)}\).
Prove that \[p^2\leq m_a^2+m_b^2+m_c^2.\]