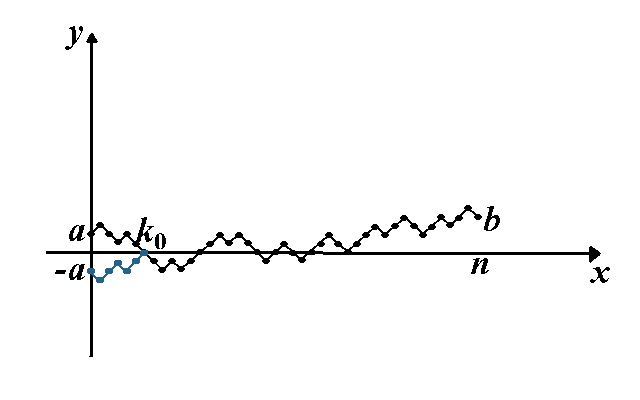Barrier Options
Random walks on integers
Let \(\Omega=\{-1,1\}^n\). Each element of \(\omega\in\Omega\) can be seen as \(\omega=(\omega_1, \dots, \omega_n)\), where \(\omega_i\in\{-1,1\}\). Let \(W_0=a\) and \(W_k(\omega)= a+\sum_{i=1}^k\omega_i\), for \(k\in\{1,2,\dots, n\}\).
Every fixed \(\omega\) uniquely determines the sequence \(W_0(\omega)\), \(W_1(\omega)\), \(W_2(\omega)\), \(\dots\), \(W_n(\omega)\) that can be graphically represented as a path in the coordinate plane.
A simple symmetric random walk is the one in which all outcomes have the same probability. The cardinality of the set \(\Omega\) is \(2^n\), i.e. \(|\Omega|=2^n\) hence for each \(\omega\in \Omega\) we have \(\mathbb P(\{\omega\})=\frac1{2^n}\).
Let us for a moment study the distribution of the endpoint \(W_n(\omega)\). Obviously, \(W_n\in\{a,a\pm 1, a\pm 2, \dots, a\pm n\}\). However, we can reduce the set of possibilities for \(W_n\) if we know whether \(n\) is even or odd. If \(2\mid n\) then there exists a positive integer \(m\) such that \(n=2m\). We then have \[W_n=W_{2m}\in\{a, a\pm 2, a\pm 4, \dots, a\pm 2m\}.\] If \(2\nmid n\) then there exists a non-negative integer \(m\) such that \(n=2m+1\). In this case we can conclude that \[W_{n}=W_{2m+1}\in\{a\pm 1, a\pm 3, a\pm 5, \dots, a\pm (2m+1)\}.\]
Recall that the definition of binomial coefficient \(\binom mr=\frac{m(m-1)\cdots (m-r+1)}{r!}\) can be extended to include \(m\in \mathbb R\) and \(n\in\mathbb N_0\). Specifically, if \(m < r\) and \(m\in\mathbb N\) then \(\binom mr=0\).
Distribution of endpoints of \(W_n(\omega)\)
Theorem 1. For every \(b\in\mathbb Z\) that satisfies \(-n+a\leq b\leq n+a\) the following identity holds:
\[\mathbb P(W_n=b)=\binom{n}{\frac12(n+b-a)}\cdot 2^{-n}.\]
Notice that each path from \(a\) to \(b\) has exactly \(n\) steps. Assume that \(u\) of these steps are \(+1\) and \(d\) of these steps are \(-1\). Then we have \begin{eqnarray*}u+d&=&n\newline
u-d&=&b-a.\end{eqnarray*}
Solving the last system gives us \(u=\frac{n+b-a}2\). Thus the total number of paths is \(\binom{n}{\frac12(n+b-a)}\) and since the probability of each of them is \(\frac1{2^n}\) we obtain the desired result.
Reflection principle
Let \(N_n(a,b)\) be the number of paths from \((0,a)\) to \((n,b)\). Let \(N_n^0(a,b)\) be the number of paths from \((0,a)\) to \((n,b)\) that contain at least one point on the \(x\)-axis (i.e. \(W_k=0\) for some \(k\in\{0,1,2,\dots, n\}\)).
Theorem 2. (Reflection principle)
For any two positive integers \(a\) and \(b\) the following holds:
\[N_n^0(a,b)=N_n(-a,b).\]
Let us denote by \(\mathcal A\) the set of all paths from \((0,a)\) to \((n,b)\) that contain points on the \(x\) axis. Let us denote by \(\mathcal B\) the set of all paths from \((0,-a)\) to \((n,b)\). The formal definitions of the sets \(\mathcal A\) and \(\mathcal B\) are:
\begin{eqnarray*}\mathcal A&=&\left\{\omega\in\Omega:\; W_0(\omega)=a,\, W_n(\omega)=b,\, \mbox{there exists }k \in\{1,2,\dots, n\}\mbox{ such that }W_k(\omega)=0\right\}.\newline
\mathcal B&=&\left\{\omega\in\Omega:\;W_0(\omega)=-a,\, W_n(\omega)=b\right\}.\end{eqnarray*}
Then we have \(N_n^0(a,b)=|\mathcal A|\) and \(N_n(-a,b)=|\mathcal B|\).
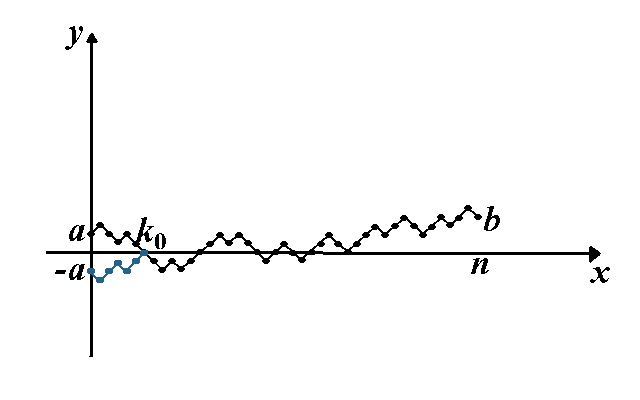
We will now construct a bijection \(\varphi:\mathcal A\to\mathcal B\). This will prove that \(|\mathcal A|=|\mathcal B|\) which would complete the proof of the lemma.
Consider \(\omega\in \mathcal A\). We know that there exists \(k\) such that \(W_k(\omega)=0\). Let us denote by \(K\) the set of all such \(k\)‘s, i.e.
\[K=\left\{k\in\{1,2,\dots, n\}:\; W_k(\omega)=0\right\}.\] Since \(K\neq \emptyset\) there is the smallest number \(k_0\) from the set \( K\), i.e. \(k_0=\min K\).
We now define
\[\varphi(\omega)=\left(-\omega_1, -\omega_2,\dots, -\omega_{k_0},\omega_{k_0+1},\omega_{k_0+2},\dots, \omega_n\right).\]
We will now prove that \(\varphi(\omega)\in \mathcal B\), and we will prove that \(\varphi\) defined in this way is one-to-one and onto.
Our first task is to establish the fact that \(\varphi(\omega)\) belongs to the set \(\mathcal B\). We need to prove that if a walk starts at \(-a\), and follows \(\varphi(\omega)\) it will end in \(b\).
It suffices to prove that \(-a-\omega_1-\cdots-\omega_{k_0}+\omega_{k_0+1}+\cdots+\omega_n=b\). The walk that starts at \(a\) and follows \(\omega\) ends at \(0\) by time \(k_0\). Also, after visiting \(0\) at time \(k_0\) the walk ends at \(b\) at time \(n\). Therefore we have that \(a+\omega_1+\cdots+\omega_{k_0}=0\) and \(\omega_{k_0+1}+\cdots+\omega_n=b\), hence
\(-a-\omega_1-\cdots-\omega_{k_0}+\omega_{k_0+1}+\cdots+\omega_n=0+\omega_{k_0+1}+\cdots+\omega_n\).
We will now prove that \(\varphi\) is one-to-one. Assume that \(\omega^1,\omega^2\in \mathcal A\) and that \(\varphi(\omega^1)=\varphi(\omega^2)\). For \(i\in\{1,2\}\), let us denote by \(k_i\) the first time that the walk starting at \(a\) and following \(\omega^i\) hits \(0\). Then we have
\(\varphi\left(\omega^i\right)=\left(-\omega^i_1,\dots, -\omega^i_{k_i},\omega^i_{k_i+1},\dots, \omega^i_n\right)\) for \(i\in\{1,2\}\). Assume that \(k_1 < k_2\). Then we have \(W_0\left(\omega^1\right)=W_0\left(\omega^2\right)\),
\(W_1\left(\omega^1\right)=W_1\left(\omega^2\right)\), \(\dots\), \(W_{k_1}\left(\omega^1\right)=W_{k_2}\left(\omega^2\right)\). Since \(W_{k_1}\left(\omega^1\right)=0\) we conclude
that \(W_{k_1}(\omega^2)=0\) which cannot happen since we assumed that \(k_2 > k_1\) is the first time that the walk hits \(0\). This contradiction proves that we can‘t have \(k_1 < k_2\). Similarly we prove that we can‘t have \(k_2 > k_1\) and we must have \(k_1=k_2\). We now have that
\[\left(-\omega^1_1,-\omega^1_2,\dots, -\omega^1_{k_1},\omega^1_{k_1+1},\dots, \omega^1_n\right)=\left(-\omega^2_1,-\omega^2_2,\dots, -\omega^2_{k_1},\omega^2_{k_1+1},\dots, \omega^2_n\right).\]
Therefore \(\omega^1_1=\omega^2_1\), \(\omega^1_2=\omega^2_2\), \(\dots\), \(\omega^1_n=\omega^2_2\) which implies that \(\omega^1=\omega^2\). This completes the proof of injectivity of \(\varphi\).
We will now prove that \(\varphi\) is surjective.
Assume that \(\hat \omega=\left(\hat\omega_1, \hat\omega_2, \dots, \hat\omega_n\right)\in \mathcal B\). We need to find \(\omega\in\mathcal A\) such that \(\varphi(\omega)=\hat \omega\). Since the walk that starts at \(-a < 0\) and follows \(\hat\omega\) ends at \(b > 0\), there must exist \(k\) such that \(W_{k}(\hat\omega)=0\). Let us denote by \(k_0\) the smallest \(k\) for which \(W_k(\hat\omega)=0\). If we denote \(\omega=\left(-\hat\omega_1, -\hat\omega_2,\dots, -\hat \omega_{k_0},\hat\omega_{k_0+1},\dots, \hat\omega_n\right)\) we can easily show that \(\varphi(\omega)=\hat\omega\).
This completes the proof of the theorem.
Corollary.
Let \(a\) and \(b\) be positive integers and \(W_m\) for \(m\in\{0,1,\dots, n\}\) a symmetric random walk.
Then
\[\mathbb P_a\left(\min_{0\leq m\leq n}W_m\leq 0, W_n=b\right)=\frac1{2^n}N(-a,b)=\mathbb P_{-a}\left(W_n=b\right),\]
where \(\mathbb P_x\) is the probability when \(W_0=x\).
Theorem 3. (Ballot theorem) Let \(b > 0\). The number of paths from \((0,0)\) to \((n,b)\) which do not visit the \(x\)-axis (apart from the starting point) is equal to \(\frac{b}nN_n(0,b)\).
We will calculate the number \(N\) of paths from \((0,0)\) to \((n,b)\) that do not visit \(0\) other than at the start. The first step of the path must be to \((1,1)\). Therefore the required number of paths is equal to the number of paths from \((1,1)\) to \((n,b)\) that do not visit \(0\). This is the same as the number of paths from \((0,1)\) to \((n-1,b)\) that do not visit \(x\) axis and can be represented as
\begin{eqnarray*}N&=&N_{n-1}(1,b)-N_{n-1}^0(1,b)=N_{n-1}(1,b)-N_{n-1}(-1,b)=\binom{n-1}{\frac12(n-1+b-1)}-\binom{n-1}{\frac12(n+b)}\newline
&=&\frac{(n-1)!}{\left(\frac{n+b-2}2\right)!\cdot \left(\frac{n-b}2\right)!}-\frac{(n-1)!}{\left(\frac{n+b}2\right)!\cdot \left(\frac{n-b-2}2\right)!}\newline
&=&\frac{(n-1)!}{\left(\frac{n-b}2\right)!\cdot \left(\frac{n+b}2\right)!}\left(\frac{n+b}2-\frac{n-b}2\right)=\frac bn \cdot \binom n{\frac{n+b}2}\newline&=&\frac bn\cdot N_n(0,b).
\end{eqnarray*}
This completes the proof of the Ballot Theorem.
Interpretation: In a city with population \(n\) everyone votes independently for one of the two candidates \(A\) or \(C\). Suppose that \(A\) scores \(a\) votes and \(C\) scores \(c\) votes (\(a+c=n\)), where \(a > c\). What is the probability that \(A\) was always in the lead.?
In this case we take \(W_0=\), vote for \(A\) is an _quot_up_quot_ movement in the random walk and vote for \(C\) is a down movement of the random walk. The final position is \(W_n=a-c=b\). We apply the ballot theorem:
\[\mathbb P\left(\left. A \mbox{ always in the lead}\right| A\mbox{ gets }a \mbox{ votes}\right)=\frac{\frac{a-c}nN_n(0,a-c)}{N_n(0,a-c)}=\frac{a-c}n=\frac{a-c}{a+c}.\]
Binomial asset pricing model
Let \(X_i\) be the random variable that is \(1\) if the stock went up in the \(i\)-th period, and \(0\) otherwise. Then the price of the stock can be expressed in terms of \(X_i\)s in the following way:
\[S_n=S\cdot u^{\sum_{i=1}^nX_i}\cdot d^{n-\sum_{i=1}^nX_i}.\]
In order to reduce the problem to the study of the random walk, let us recall that \(\Omega=\{-1,1\}^n\) and let us assume that \[\mathbb P(\omega)=p^{k_{\omega}}(1-p)^{n-k_{\omega}},\] where \(k_{\omega}\) is the number of \(+1\)‘s in \(\omega\).
We can now set \(X_i=\frac{\omega_i+1}2\), and obtain
\begin{eqnarray*}S_n&=&S\cdot u^{\frac12W_n+\frac n2}\cdot d^{\frac n2-\frac{W_n}2}=S\left(\frac ud\right)^{\frac12W_n}\cdot \left(ud\right)^{\frac n2}\newline&=&
Se^{W_n\cdot\frac{\ln u-\ln d}2+\frac{n(\ln u+\ln d)}2}.\end{eqnarray*}
For simplicity, let us assume that \(ud=1\). Then \(S_n=Se^{\ln uW_n}\).
We will consider up-and-out call option with maturity time \(n\) with the payoff:
\[\mbox{Payoff} = \left(S_n-K\right)^+\cdot 1_{S_n^* < B},\]
where \(K\) is the strike, \(B\) is the barrier, and \(S_n^*=\max_{0\leq m\leq n}S_m\).
We will use two methods to price such an option.
- \(1^{\circ}\) First method. This is a forward method based on _quot_path counting._quot_ This method uses reflection principle and allows for closed form formulas. It can be extended to continuous setting into Black-Scholes model.
- \(2^{\circ}\) Second method. This is a backward recursive method. It does not result in closed formulas but in an algorithm. This method can be used for a variety of options, including the American options. Continuous time generalizations lead to the principle of dynamic programming in optimization.
We will consider the following numeric example. Let \(u=1.25\), \(d=0.8\), \(S=60\), \(r=0.05\), \(n=4\), \(K=90\), \(B=115\).
Then the stock price tree and the payoffs of the option are given in the following table:
\[
\begin{array}{llllll}
&&&&146.484375&0\newline
&&&117.1875&&\newline
&&93.75&&93.75&3.75\newline
&75&&75&&\newline
60&&60&&60&0\newline
&48&&48&&\newline
&&38.4&&38.4&0\newline
&&&30.72&&\newline
&&&&24.576&0\end{array}
\]
Then we obtain \(p_*=\frac{1+r-d}{u-d}=0.555555556\).
- \(1^{\circ}\) First method. The price is given by:
\begin{eqnarray*}
\mbox{Price}&=&\frac1{(1+r)^4}\mathbb E_*\left[\mbox{Payoff}\right]\newline&=&\frac1{1.05^4}\cdot 3.75\cdot \left(p_*\right)^3\cdot \left(1-p_*\right)^1\cdot \left(\mbox{Number of paths that end up at }93.75\mbox{ and stay below }115\right)\newline
&=&\frac1{1.05^4}\cdot 3.75\cdot \left(0.555555556\right)^3\cdot 0.444444444\cdot 3\newline&=&0.705334769.
\end{eqnarray*}
- \(2^{\circ}\) Second method. Let \(\Pi_{i,j}\) denote the value of the option after \(i\) periods if the stock went up \(j\) times. We have that
\(\Pi_{4,0}=\Pi_{4,1}=\Pi_{4,2}=0\), \(\Pi_{4,3}=3.75\), \(\Pi_{4,4}=0\). We now calculate backwards the price of the option. The option price tree is now given by the following table
\[
\begin{array}{lllll}
&&&&0\newline
&&&0&\newline
&&0.83984211&&3.75\newline
&0.888721809&&1.984126984&\newline
0.705334769&&1.049802637&&0\newline
&0.555451131&&0&\newline
&&0&&0\newline
&&&0&\newline
&&&&0
\end{array}
\]
Let us point out that \(\Pi_{3,3}=0\) because the stock hits the barrier at time \(3\) if it went up in each of the periods. For every other cell in the table, the price is calculated in the standard way.
We will now explain how in general the method 1 can be used to calculate the price of the option. The price is given by
\[\mbox{Price}= \frac1{(1+r)^n}\mathbb E_*\left[\left(S_n-K\right)^+\cdot 1_{S_n^* < B}\right].\] The expectation can be now calculated in the following way:
\begin{eqnarray*}
\mathbb E_*\left[\left(S_n-K\right)^+\cdot 1_{S_n^* < B}\right]&=&\sum_{b:K < b < B}(b-K)\cdot\mathbb P_*\left(S_n^* < B,S_n=b\right).
\end{eqnarray*}
Let us now use that \(S_n=Se^{\ln uW_n}\). Therefore \(S_n=b\) can be re-written as \(W_n=\frac{\ln b-\ln S}{\ln u}\). Similarly, \(S_n < B\) can be written in an equivalent form as \(W_n^* < \frac{\ln B-\ln S}{\ln u}\). Thus
\[\mbox{Price}= \frac1{(1+r)^n}\cdot \sum_{K < b < B}(b-K)\mathbb P_*\left(W_n^* < \frac{\ln B-\ln S}{\ln u}, W_n=\frac{\ln b-\ln S}{\ln u}\right).\]
Problem 1.
Assume that the stock price follows binomial model with \(n=50\) steps. The initial price of the stock at time \(0\) is \(S_0=1024\) and in each step the price of the stock goes up by the factor \(u=1.25\) or down by the factor \(d=0.8\). The simple interest rate in each period is \(r=10\%\). Determine the price of the derived security that pays USD \(1\) if the price of the stock at time \(n\) is exactly \(2500\) and during the entire time interval \([0,50]\) the stock has never reached the level \(3125\) or gone over the level \(3125\).
The risk-neutral probabilities are \(p_*=\frac{1+r-d}{u-d}=\frac23\) and \(q_*=\frac{u-(1+r)}{u-d}=\frac13\).
\[P_0=\frac1{(1+r)^{n}}\mathbb E_*\left[\mbox{Payoff}\right]=\frac1{1.1^{50}}\cdot\mathbb E_*\left[\mbox{Payoff}\right].\]
In order for the payoff to be non-zero the price of the stock has to be exactly \(2500=S_0\cdot u^4\) which means that the stock must make exactly \(27\) up movements, and \(23\) down movements. In addition, at no time should the stock price raise to or above the level \(B=3125= S_0\cdot u^5\). The last condition means that for every \(k\in\left\{1,2,\dots, 50\right\}\) the difference between the number of up movements by time \(k\) and the number of down movements by time \(k\) should be less than \(b=5\).
Let us denote by \(G\) the set of all paths from \((0,0)\) to \((50,4)\) that stay below the level \(5\). We know that by reflection principle we have \(|G|=\binom{50}{27}-\binom{50}{28}\).
Therefore \[P_0=\frac1{1.1^{50}}\cdot\left(\binom{50}{27}-\binom{50}{28}\right)\cdot {p_*}^{{27}}\cdot {q_*}^{{23}}=
\frac1{1.1^{50}}\cdot\left(\binom{50}{27}-\binom{50}{28}\right)\cdot \frac{2^{27}}{3^{50}}.
\]