Geometry
If \(ABCD\) is a parallelogram, prove that \[AB^2+BC^2+CD^2+DA^2=AC^2+BD^2.\]
Let \(ABC\) be a triangle such that \(\angle CAB=\angle CBA=\alpha\). Assume that the incircle of the triangle touches the sides \(AB\) and \(AC\) in \(C^{\prime}\) and \(B^{\prime}\) respectively. Assume that \(I\) is the incenter of \(\triangle ABC\) and that \(AC’=x\). Find an expression, in terms of \(x\) and \(\alpha\), for the area of the curvilinear triangle bounded by the lines \(AB\) and \(AC\) and the arc of the incircle between \(C’\) and \(B’\).
Assume that a square is inscribed in a triangle such that all three vertices of the square belong to the edges of the triangle. Show that the area of the square is at most half of the area of the triangle.
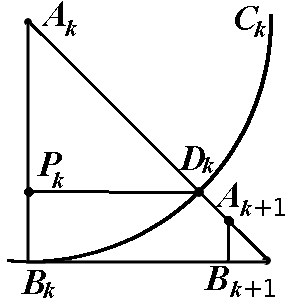
Consider an infinite sequence of circles \((C_k)_{k=0}^{\infty}\) defined in the following way: The circle \(C_0\) has center \((1,1)\) and is tangent to the \(x\) and \(y\) axis. For \(k\geq 0\) the circle \(C_{k+1}\) is defined to be the circle externally tangent to \(C_k\), tangent to the \(x\) axis, and with the center on the segment connecting \((1,1)\) to \((2,0)\). Denote by \(d_k\) the radius of \(C_k\). Evaluate \(\displaystyle \sum_{k=0}^{\infty} d_k\).
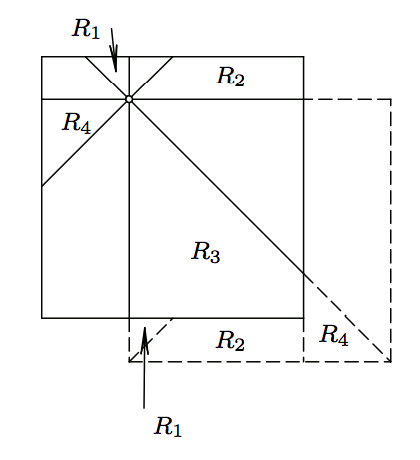
Every point in the plane is painted in blue or red. Show that there are either two blue points at the distance exactly one, or four colinear red points \(R_1\), \(R_2\), \(R_3\), and \(R_4\) such that \(R_1R_2=R_2R_3=R_3R_4=1\).
Let \(ABCD\) be a rectangle. Let \(E\) be the foot of perpendicular from \(A\) to \(BD\). Let \(F\) be an arbitrary point of the diagonal \(BD\) between \(D\) and \(E\). Let \(G\) be the intersection of the line \(CF\) with the perpendicular from \(B\) to \(AF\). Let \(H\) be the intersection of the line \(BC\) with the perpendicular from \(G\) to \(BD\). Prove that \(\sphericalangle EGB=\sphericalangle EHB\).
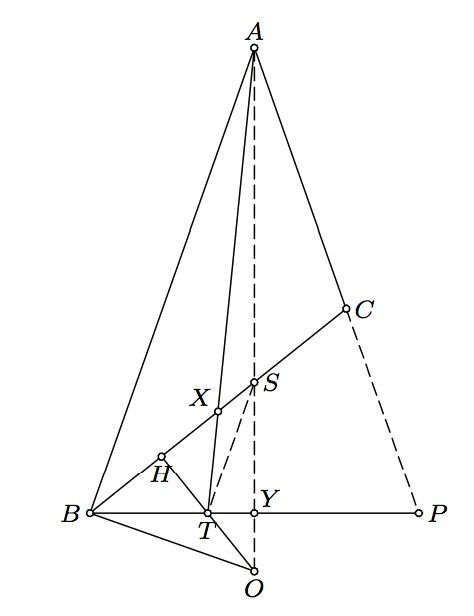
Given a triangle \(ABC\), consider a circle \(k\) that is tangent to the lines \(AB\) and \(AC\) at \(B\) and \(P\). Let \(H\) be the foot of perpendicular from the center \(O\) of \(k\) to the line \(BC\), and let \(T\) be the intersection of \(OH\) and \(BP\). Prove that \(AT\) bisects the segment \(BC\).
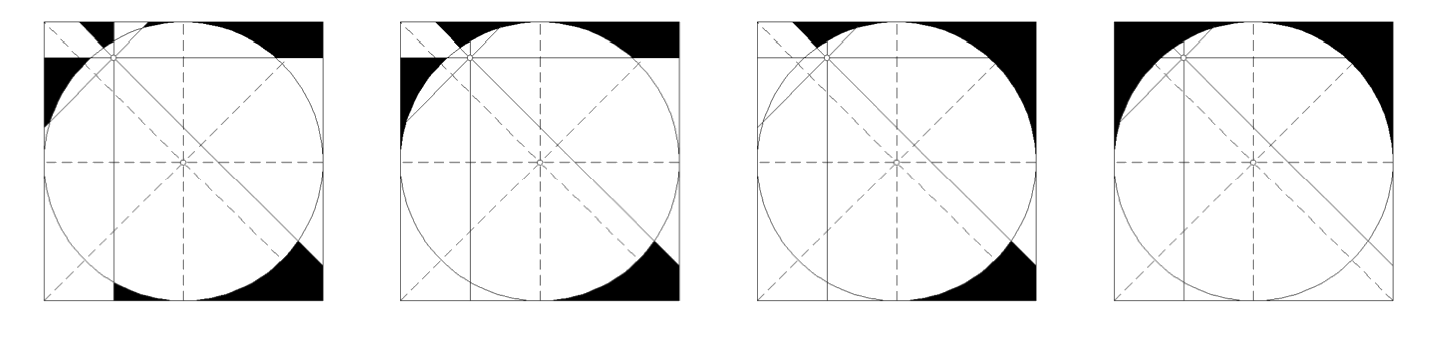
Let \(K\) be the point \(K\) in the interior of the unit circle. The circle is divided into \(8\) regions using four lines passing through \(K\) such that each two adjacent lines form an angle of \(45^{\circ}\), as shown in the picture. Four of these regions are colored such that no two colored regions share more than one point. Prove that the area of the colored regions is exactly half the area of the circle.