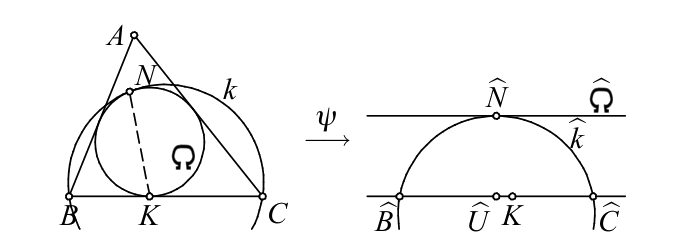Olympiad training materials (main page)
Inversion
Dušan Đukić
Introduction
An
inversion with respect to a given circle (sphere) is the map sending each point \(A\) other than the center \(O\) of the circle to the point \(A'\) on ray \(OA\) such that \(OA '=r^2/OA\). What makes this map useful is the fact that it preserves angles and maps lines and circles onto lines or circles. Thus appropriate inversions can reduce the number of unpleasant circles (mapping them to lines) and often even turn a difficult problem into a quite simple one, as we show on a number of solved problems. Problems range from Ptolemy's inequality, to Feuerbach's theorem, and some of the hardest problems appearing on math competitions.
General properties
Inversion \(\Psi\) is a map of a plane or space without a fixed
point \(O\) onto itself, determined by a circle \(k\) with center \(O\)
and radius \(r\), which takes point \(A\neq O\) to the point
\(A' =\Psi(A)\) on the ray \(OA\) such that \(OA\cdot OA' =r^2\).
From now on, unless noted otherwise, \(X' \) always denotes the image
of object \(X\) under a considered inversion.
Clearly, map \(\Psi\) is continuous and inverse to itself, and maps
the interior and exterior of \(k\) to each other, which is why it is
called ``inversion_quot_. The next thing we observe is that \(\triangle
P' OQ' \sim\triangle QOP\) for all point \(P,Q\neq O\)
(for \(\angle P' OQ' =\angle QOP\) and \(OP' /OQ' =(r^2/OP)/(r^2/OQ)=
OQ/OP\)), with the ratio of similitude \(\frac{r^2}{OP\cdot OQ}\). As
a consequence, we have \[\angle OQ' P' =\angle OPQ\quad\mbox{and}
\quad P' Q' =\frac{r^2}{OP\cdot OQ}PQ.\]
What makes inversion attractive is the fact that it maps lines and
circles into lines and circles. A line through \(O\) (\(O\) excluded)
obviously maps to itself. What if a line \(p\) does not contain \(O\)?
Let \(P\) be the projection of \(O\) on \(p\) and \(Q\in p\) an arbitrary
point of \(p\). Angle \(\angle OPQ=\angle OQ' P' \) is right, so \(Q' \)
lies on circle \(k\) with diameter \(OP' \). Therefore \(\Psi(p)=k\) and
consequently \(\Psi(k)=p\). Finally, what is the image of a circle
\(k\) not passing through \(O\)? We claim that it is also a circle; to
show this, we shall prove that inversion takes any four concyclic
points \(A,B,C,D\) to four concyclic points \(A' ,B' ,C' ,D' \). The
following angles are regarded as oriented. Let us show that
\(\angle A' C' B' =\angle A' D' B' \). We have \(\angle A' C' B' =\angle OC' B'
-\angle OC' A' =\angle OBC-\angle OAC\) and analogously \(\angle
A' D' B' =\angle OBD-\angle OAD\), which implies \(\angle A' D' B' -\angle
A' C' B' =\angle CBD-\angle CAD=0\), as we claimed. To sum up:
- A line through \(O\) maps to itself.
- A circle through \(O\) maps to a line not
containing \(O\) and vice-versa.
- A circle not passing through \(O\) maps to a circle
not passing through \(O\) (not necessarily the same).
Remark. Based on what we have seen, it can be noted that
inversion preserves angles between curves, in particular circles or
lines. Maps having this property are called
conformal.
When should inversion be used? As always, the answer comes with
experience and cannot be put on a paper. Roughly speaking,
inversion is useful in destroying ``inconvenient_quot_ circles and
angles on a picture. Thus, some pictures ``cry_quot_ to be inverted:
- There are many circles and lines through the same
point \(A\). Invert through \(A\).
Example (IMO 2003, Shortlist)
Let \(\Gamma_1,\Gamma_2,\Gamma_3,\Gamma_4\) be distinct circles such
that \(\Gamma_1,\Gamma_3\) are externally tangent at \(P\), and
\(\Gamma_2,\Gamma_4\) are externally tangent at the same point \(P\).
Suppose that \(\Gamma_1\) and \(\Gamma_2\); \(\Gamma_2\) and \(\Gamma_3\);
\(\Gamma_3\) and \(\Gamma_4\); \(\Gamma_4\) and \(\Gamma_1\) meet at
\(A,B,C,D\), respectively, and that all these points are different
from \(P\). Prove that
\[\frac{AB\cdot BC}{AD\cdot DC}=\frac{PB^2}{PD^2}.
\]
Apply the inversion with center
at \(P\) and radius \(r\); let \(\widehat{X}\) denote the image of \(X\).
The circles \(\Gamma_1,\Gamma_2,\Gamma_3,\Gamma_4\) are transformed
into lines
\(\widehat{\Gamma_1},\widehat{\Gamma_2},\widehat{\Gamma_3},
\widehat{\Gamma_4}\), where \(\widehat{\Gamma_1}\parallel\widehat
{\Gamma_3}\) and \(\widehat{\Gamma_2}\parallel\widehat{\Gamma_4}\), and
therefore \(\widehat{A}\widehat{B}\widehat{C}\widehat{D}\) is a
parallelogram. Further, we have \( AB=\frac{r^2}{P\widehat{A}
\cdot P\widehat{B}}\widehat{A}\widehat{B}\), \( PB=\frac{r^2}
{P\widehat{B}}\), etc. The equality to be proven becomes
\[\frac{P\widehat{D}^2}{P\widehat{B}^2}\cdot\frac
{\widehat{A}\widehat{B}\cdot\widehat{B}\widehat{C}}
{\widehat{A}\widehat{D}\cdot\widehat{D}\widehat{C}}=
\frac{P\widehat{D}^2}{P\widehat{B}^2},\] which holds because
\(\widehat{A}\widehat{B}=\widehat{C}\widehat{D}\) and
\(\widehat{B}\widehat{C}=\widehat{D}\widehat{A}\).
- There are many angles \(\angle AXB\) with fixed
\(A,B\). Invert through \(A\) or \(B\).
Example (IMO 1996, problem 2)
Let \(P\) be a point inside \(\triangle ABC\) such that \(\angle
APB-\angle C=\angle APC-\angle B\). Let \(D,E\) be the incenters of
\(\triangle APB,\triangle APC\) respectively. Show that \(AP\), \(BD\),
and \(CE\) meet in a point.
Apply an inversion with center
at \(A\) and radius \(r\). Then the given condition becomes \(\angle
B' C' P' = \angle C' B' P' \), i.e., \(B' P' =P' C' \). But \(P' B' =\frac{r^2}
{AP\cdot AB}PB\), so \(AC/AB=PC/PB\).
Caution: Inversion may also bring new inconvenient circles and
angles.
Problems
Problem 1 Circles \(k_1,k_2,k_3,k_4\) are such that \(k_2\) and \(k_4\) each
touch \(k_1\) and \(k_3\). Show that the tangency points are collinear
or concyclic.
Let \(k_1\) and \(k_2\), \(k_2\) and \(k_3\), \(k_3\) and
\(k_4\), \(k_4\) and \(k_1\) touch at \(A,B,C,D\), respectively. An
inversion with center \(A\) maps \(k_1\) and \(k_2\) to parallel lines
\(k_1' \) and \(k_2' \), and \(k_3\) and \(k_4\) to circles \(k_3' \) and \(k_4' \)
tangent to each other at \(C' \) and tangent to \(k_2' \) at \(B' \) and to
\(k_4' \) at \(D' \). It is easy to see that \(B' ,C' , D' \) are collinear.
Therefore \(B,C,D\) lie on a circle through \(A\).
Problem 2
Prove that for any points \(A,B,C,D\), \(AB\cdot CD+BC\cdot DA
\geq AC\cdot BD\), and that equality holds if and only if \(A,B,C,D\)
are on a circle or a line in this order. (Ptolemy's
inequality)
Applying the inversion with center \(A\) and radius \(r\) gives
\(AB=\frac{r^2}{AB' }\), \(CD=\frac{r^2}{AC' \cdot AD' } C' D' \), etc. The
required inequality reduces to \(C' D' +B' C' \geq B' D' \).
Problem 3
Let \(\omega\) be the semicircle with diameter \(PQ\). A circle
\(k\) is tangent internally to \(\omega\) and to segment \(PQ\) at \(C\).
Let \(AB\) be the tangent to \(k\) perpendicular to \(PQ\), with \(A\) on
\(\omega\) and \(B\) on segment \(CQ\). Show that \(AC\) bisects the angle
\(\angle PAB\).
Invert through \(C\). Semicircle \(\omega\) maps to the
semicircle \(\omega' \) with diameter \(P' Q' \), circle \(k\) to the tangent
to \(\omega' \) parallel to \(P' Q' \), and line \(AB\) to a circle \(l\)
centered on \(P' Q' \) which touches \(k\) (so it is congruent to the
circle determined by \(\omega' \)). Circle \(l\) intersects \(\omega' \) and
\(P' Q' \) in \(A' \) and \(B' \) respectively. Hence \(P' A' B' \) is an isosceles
triangle with \(\angle PAC=\angle A' P' C= \angle A' B' C=\angle BAC\).
Problem 4
Points \(A,B,C\) are given on a line in this order.
Semicircles \(\omega,\omega_1,\omega_2\) are drawn on \(AC,AB\), \(BC\)
respectively as diameters on the same side of the line. A sequence
of circles \((k_n)\) is constructed as follows: \(k_0\) is the circle
determined by \(\omega_2\) and \(k_n\) is tangent to \(\omega,\omega_1,
k_{n-1}\) for \(n\geq1\). Prove that the distance from the center of
\(k_n\) to \(AB\) is \(2n\) times the radius of \(k_n\).
Under the inversion with center \(A\) and squared radius
\(AB\cdot AC\) points \(B\) and \(C\) exchange positions, \(\omega\) and
\(\omega_1\) are transformed to the lines perpendicular to \(BC\) at \(C\)
and \(B\), and the sequence \((k_n)\) to the sequence of circles
\((k_n' )\) inscribed in the region between the two lines. Obviously,
the distance from the center of \(k_n' \) to \(AB\) is \(2n\) times its
radius. Since circle \(k_n\) is homothetic to \(k_n' \) with respect to
\(A\), the statement immediately follows.
Problem 5
A circle with center \(O\) passes
through points \(A\) and \(C\) and intersects the sides \(AB\) and \(BC\)
of the triangle \(ABC\) at points \(K\) and \(N\), respectively. The
circumscribed circles of the triangles \(ABC\) and \(KBN\) intersect
at two distinct points \(B\) and \(M\). Prove that \(\measuredangle
OMB=90^{\circ}.\) (IMO 1985-5.)
Invert through \(B\). Points \(A' ,C' ,M' \) are collinear and so are
\(K' ,N' ,M' \), whereas \(A' ,C' ,N' \), \(K' \) are on a circle. What does the
center \(O\) of circle \(ACNK\) map to? Inversion does not preserve
centers. Let \(B_1\) and \(B_2\) be the feet of the tangents from \(B\)
to circle \(ACNK\). Their images \(B_1' \) and \(B_2' \) are the feet of the
tangents from \(B\) to circle \(A' C' N' K' \), and since \(O\) lies on the
circle \(BB_1B_2\), its image \(O' \) lies on the line \(B_1' B_2' \) - more
precisely, it is at the midpoint of \(B_1' B_2' \). We observe that \(M' \)
is on the polar of point \(B\) with respect to circle \(A' C' N' K' \),
which is nothing but the line \(B_1B_2\). It follows that \(\angle
OBM=\angle BO' M' =\angle BO' B_1' =90^{\circ}\).
Problem 6
Let \(p\) be the semiperimeter of a triangle \(ABC\). Points
\(E\) and \(F\) are taken on line \(AB\) such that \(CE=CF=p\). Prove that
the circumcircle of \(\triangle EFC\) is tangent to the excircle
of \(\triangle ABC\) corresponding to \(AB\).
The inversion with center \(C\) and radius \(p\) maps points \(E\)
and \(F\) and the excircle to themselves, and the circumcircle of
\(\triangle CEF\) to line \(AB\) which is tangent to the excircle. The
statement follows from the fact that inversion preserves tangency.
Problem 7
Prove that the nine-point circle of triangle \(ABC\) is
tangent to the incircle and all three excircles. (Feuerbach's
theorem)
We shall show that the nine-point circle \(\epsilon\) touches the
incircle \(k\) and the excircle \(k_a\) across \(A\). Let \(A_1,B_1,C_1\) be
the midpoints of \(BC,CA,AB\), and \(P,Q\) the points of tangency of \(k\)
and \(k_a\) with \(BC\), respectively. Recall that \(A_1P=A_1Q\); this
implies that the inversion with center \(A_1\) and radius \(A_1P\) takes
\(k\) and \(k_a\) to themselves. This inversion also takes \(\epsilon\) to
a line. It is not difficult to prove that this line is symmetric to
\(BC\) with respect to the angle bisector of \(\angle BAC\), so it also
touches \(k\) and \(k_a\).
Problem 8
The incircle of a triangle \(ABC\) is tangent to \(BC,CA,AB\) at
\(M,N\) and \(P\), respectively. Show that the circumcenter and
incenter of \(\triangle ABC\) and the orthocenter of \(\triangle MNP\)
are collinear.
The incenter of \(\triangle ABC\) and the orthocenter of
\(\triangle MNP\) lie on the Euler line of the triangle
\(ABC\). The
inversion with respect to the incircle of \(ABC\) maps points \(A,B,C\)
to the midpoints of \(NP,PM,MN\), so the circumcircle of \(ABC\) maps to
the nine-point circle of \(\triangle MNP\) which is also centered on
the Euler line of \(MNP\). It follows that the center of circle \(ABC\)
lies on the same line.
Problem 9
Points \(A,B,C\) are given in this order on a line. Semicircles
\(k\) and \(l\) are drawn on diameters \(AB\) and \(BC\) respectively, on
the same side of the line. A circle \(t\) is tangent to \(k\), to \(l\)
at point \(T\neq C\), and to the perpendicular \(n\) to \(AB\) through
\(C\). Prove that \(AT\) is tangent to \(l\).
An inversion with center \(T\) maps circles \(t\) and \(l\) to
parallel lines \(t' \) and \(l' \), circle \(k\) and line \(n\) to circles
\(k' \) and \(n' \) tangent to \(t' \) and \(l' \) (where \(T\in n' \)), and line
\(AB\) to circle \(a' \) perpendicular to \(l' \) (because an inversion
preserves angles) and passes through \(B' ,C' \in l' \); thus \(a' \) is the
circle with diameter \(B' C' \). Circles \(k' \) and \(n' \) are congruent and
tangent to \(l' \) at \(B' \) and \(C' \), and intersect \(a' \) at \(A' \) and \(T\)
respectively. It follows that \(A' \) and \(T\) are symmetric with
respect to the perpendicular bisector of \(B' C' \) and hence
\(A' T\parallel l' \), so \(AT\) is tangent to \(l\).
Problem 10
Let \(A_1A_2A_3\) be a nonisosceles triangle with
incenter \(I\). Let \(C_i\), \(i=1,2,3\), be the smaller circle through
\(I\) tangent to \(A_iA_{i+1}\) and \(A_iA_{i+2}\) (the addition of
indices being mod 3). Let \(B_i\), \(i=1,2,3\), be the second point of
intersection of \(C_{i+1}\) and \(C_{i+2}\). Prove that the
circumcenters of the triangles \(A_1B_1I,A_2B_2I,A_3B_3I\) are
collinear. (IMO 1997 Shortlist)
The centers of three circles passing through the same point
\(I\) and not touching each other are collinear if and only if they
have another common point. Hence it is enough to show that the
circles \(A_iB_iI\) have a common point other than \(I\). Now apply
inversion at center \(I\) and with an arbitrary power. We shall denote
by \(X' \) the image of \(X\) under this inversion. In our case, the
image of the circle \(C_i\) is the line \(B_{i+1}' B_{i+2}' \) while the
image of the line \(A_{i+1}A_{i+2}\) is the circle \(IA_{i+1}' A_{i+2}' \)
that is tangent to \(B_i' B_{i+2}' \), and \(B_i' B_{i+2}' \). These three
circles have equal radii, so their centers \(P_1,P_2,P_3\) form a
triangle also homothetic to \(\triangle B_1' B_2' B_3' \). Consequently,
points \(A_1' ,A_2' ,A_3' \), that are the reflections of \(I\) across the
sides of \(P_1P_2P_3\), are vertices of a triangle also homothetic to
\(B_1' B_2' B_3' \). It follows that \(A_1' B_1' ,A_2' B_2' ,A_3' B_3' \) are
concurrent at some point \(J' \), i.e., that the circles \(A_iB_iI\) all
pass through \(J\).
Problem 11
If seven vertices of a hexahedron lie on a sphere, then so
does the eighth vertex.
Let \(AYBZ,AZCX,AXDY,WCXD,WDYB,WBZC\) be the faces of the
hexahedron, where \(A\) is the ``eighth_quot_ vertex. Apply an inversion
with center \(W\). Points \(B' ,C' ,D' \), \(X' ,Y' ,Z' \) lie on some plane
\(\pi\), and moreover, \(C' ,X' ,D' \); \(D' ,Y' ,B' \); and \(B' ,Z' ,C' \) are
collinear in these orders. Since \(A\) is the intersection of the
planes \(YBZ,ZCX,XDY\), point \(A' \) is the second intersection point of
the spheres \(WY' B' Z' ,WZ' C' X' ,WX' D' Y' \). Since the circles
\(Y' B' Z' ,Z' C' X' \), \(X' D' Y' \) themselves meet at a point on plane \(\pi\),
this point must coincide with \(A' \). Thus \(A' \in\pi\) and the
statement follows.
Problem 12
A sphere with center on the plane of the face \(ABC\) of a
tetrahedron \(SABC\) passes through \(A,B\) and \(C\), and meets the
edges \(SA,SB,SC\) again at \(A_1,B_1,C_1\), respectively. The planes
through \(A_1,B_1,C_1\) tangent to the sphere meet at a point \(O\).
Prove that \(O\) is the circumcenter of the tetrahedron \(SA_1B_1C_1\).
Apply the inversion with center \(S\) and squared radius \(SA
\cdot SA_1=SB\cdot SB_1=SC\cdot SC_1\). Points \(A\) and \(A_1\), \(B\) and
\(B_1\), and \(C\) and \(C_1\) map to each other, the sphere through
\(A,B,C,A_1,B_1,C_1\) maps to itself, and the tangent planes at
\(A_1,B_1,C_1\) go to the spheres through \(S\) and \(A\), \(S\) and \(B\),
\(S\) and \(C\) which touch the sphere \(ABCA_1B_1C_1\). These three
spheres are perpendicular to the plane \(ABC\), so their centers lie
on the plane \(ABC\); hence they all pass through the point
\(\overline{S}\) symmetric to \(S\) with respect to plane \(ABC\).
Therefore \(\overline{S}\) is the image of \(O\). Now since \(\angle
SA_1O=\angle S\overline{S}A=\angle\overline{S}SA=\angle OSA_1\), we
have \(OS=OA_1\) and analogously \(OS=OB_1=OC_1\).
Problem 13
Let \(KL\) and \(KN\) be the tangents from a point \(K\) to a
circle \(k\). Point \(M\) is arbitrarily taken on the extension of
\(KN\) past \(N\), and \(P\) is the second intersection point of \(k\)
with the circumcircle of triangle \(KLM\). The point \(Q\) is the
foot of the perpendicular from \(N\) to \(ML\). Prove that
\(\angle MPQ=2\angle KML\).
Apply the inversion with center \(M\). Line \(MN' \) is tangent to
circle \(k' \) with center \(O' \), and a circle through \(M\) is tangent to
\(k' \) at \(L' \) and meets \(MN' \) again at \(K' \). The line \(K' L' \)
intersects \(k' \) at \(P' \), and \(N' O' \) intersects \(ML' \) at \(Q' \). The
task is to show that \(\angle MQ' P' = \angle L' Q' P' =2\angle K' ML' \).
Let the common tangent at \(L' \) intersect \(MN' \) at \(Y' \). Since the
peripheral angles on the chords \(K' L' \) and \(L' P' \) are equal (to
\(\angle K' L' Y' \)), we have \(\angle L' O' P' =2\angle L' N' P' =2\angle
K' ML' \). It only remains to show that \(L' ,P' ,O' ,Q' \) are on a circle.
This follows from the equality \(\angle O' Q' L' =90^{\circ}- \angle
L' MK' =90^{\circ}-\angle L' N' P' =\angle O' P' L' \) (the angles are
regarded as oriented).
Problem 14
The incircle \(\Omega\) of the acute-angled triangle
\(ABC\) is tangent to \(BC\) at \(K\). Let \(AD\) be an altitude of
triangle \(ABC\) and let \(M\) be the midpoint of \(AD\). If \(N\) is the
other common point of \(\Omega\) and \(KM\), prove that \(\Omega\) and
the circumcircle of triangle \(BCN\) are tangent at \(N\).
(IMO 2002 Shortlist)
Let \(k\) be the circle through \(B,C\) that is tangent
to the circle \(\Omega\) at point \(N' \). We must prove that \(K,M,N' \)
are collinear. Since the statement is trivial for \(AB=AC\), we may
assume that \(AC > AB\). As usual, \(R,r,\alpha,\beta,\gamma\) denote the
circumradius and the inradius and the angles of \(\triangle ABC\),
respectively.
We have \(\tan\angle BKM=DM/DK\). Straightforward calculation gives
\( DM=\frac12AD=R\sin\beta\sin\gamma\) and \(
DK=\frac{DC-DB}2-\frac
{KC-KB}2=R\sin(\beta-\gamma)-R(\sin\beta-\sin\gamma)=4R\sin\frac
{\beta-\gamma}2\sin\frac{\beta}2\sin\frac{\gamma}2\), so we obtain
\[\tan\angle BKM=\frac{\sin\beta\sin\gamma}
{4\sin\frac{\beta-\gamma}2\sin\frac{\beta}2\sin\frac{\gamma}2}=
\frac{\cos\frac{\beta}2\cos\frac{\gamma}2}{\sin\frac{\beta-\gamma}
2}.\]
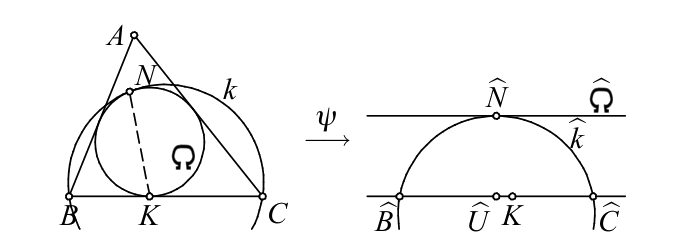
To calculate the angle
\(BKN' \), we apply the inversion \(\psi\) with center at \(K\) and power
\(BK\cdot CK\). For each object \(X\), we denote by \(\widehat{X}\) its
image under \(\psi\). The incircle \(\Omega\) maps to a
line \(\widehat{\Omega}\) parallel to
\(\widehat{B}\widehat{C}\), at distance \(\frac{BK\cdot CK}{2r}\)
from \(\widehat{B}\widehat{C}\). Thus the point \(\widehat{N' }\) is the
projection of the midpoint \(\widehat{U}\) of \(\widehat{B}
\widehat{C}\) onto \(\widehat{\Omega}\). Hence \[ \tan\angle BKN' =\tan
\angle\widehat{B}K\widehat{N' }=\frac{\widehat{U}\widehat{N' }}
{\widehat{U}K}=\frac{BK\cdot CK}{r(CK-BK)}.\] Again, one easily
checks that \(KB\cdot KC=bc\sin^2\frac{\alpha}2\) and \(
r=4R\sin\frac{\alpha}2\cdot \sin\frac{\beta}2\cdot
\sin\frac{\gamma}2\), which implies \begin{eqnarray*}\tan\angle
BKN' &=&\frac{bc\sin^2\frac{\alpha}2}{r(b-c)}\&=&\frac{4R^2\sin
\beta\sin\gamma\sin^2\frac{\alpha}2}{4R\sin\frac{\alpha}2\sin
\frac{\beta}2\sin\frac{\gamma}2\cdot2R(\sin\beta-\sin\gamma)}=
\frac{\cos\frac{\beta}2\cos\frac{\gamma}2}{\sin\frac{\beta-\gamma}
2}.\end{eqnarray*} Hence \(\angle BKM=\angle BKN' \), which implies
that \(K,M,N' \) are indeed collinear; thus \(N' \equiv N\).