Midterm 2 (Practice 4)
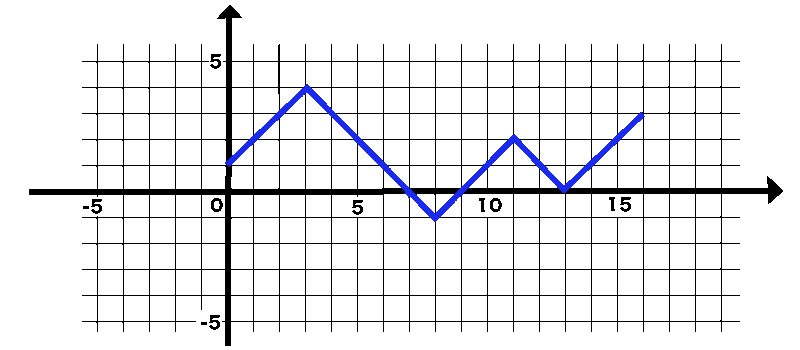
Consider the path of the random walk that starts from the point \( (0,1) \) and corresponds to the sequence \[ \omega=\left(+1,+1,+1,-1,-1, -1,-1, -1, +1,+1,+1,-1,-1,+1,+1,+1\right).\]
- (a) Sketch the described path.
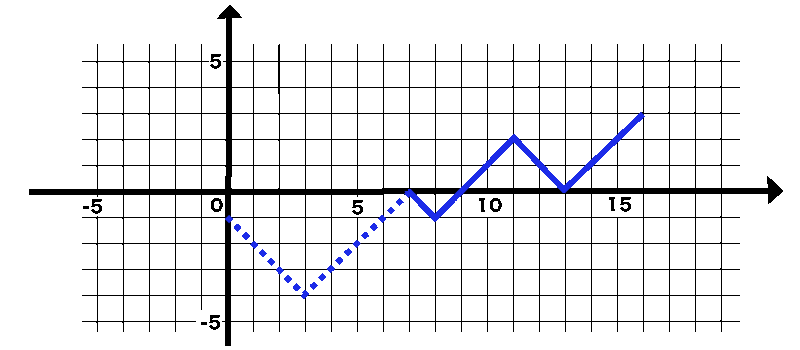
- (b) Determine the path \( \hat\omega \) that is obtained from the path \( \omega \) using the reflection principle.
- (c) Draw the path that corresponds to \( \hat\omega \).
Assume an one period binomial model in which the initial stock price is \( S=80 \) and in each period the stock price can go either up by a factor of \( u=\frac{7}{4} \) or down by a factor of \( d=\frac{3}{4} \). Assume that the simple interest rate over one time period is \( r=\frac{1}{4} \).
- (a) Determine the fair price of the European call option with strike \( K=80 \).
- (b) Assume that instead of the price determined in part (a), the European call option is trading at \( 18 \). Prove that there is an arbitrage and explain how the arbitrage can be achieved.
There are two portfolios \( A \) and \( B \) consisting of European put and call options written on the same underlying asset and with the same expiration.
- The portfolio \( A \) consists of \( 5 \) European put options with strike \( {USD} 145 \), \( 9 \) European call options with strike \( {USD} 145 \), and 7 European put options with strike \( {USD} 125 \).
- The portfolio \( B \) consists of \( 7 \) European put options with strike \( {USD} 135 \), \( 9 \) European call options with strike \( {USD} 135 \), and \( 5 \) European put options with strike \( {USD} 155 \).
For each \( k\in\{0,1,2,\dots, 30\} \) the symbol \( S(k) \) denotes the price of the stock at time \( k \). A European call option with strike \( {USD} 90 \) and expiration \( n=30 \) costs \( {USD} 15 \). A European put option with strike \( {USD} 100 \) and expiration \( 30 \) costs \( {USD} 11 \). Both options have the same stock as their underlying security. What is the price of the security whose payoff structure is \begin{eqnarray*} \mbox{Payoff} &=&\left\{\begin{array}{rl} 7 S(30)-{USD} 630,&\mbox{if }S(30)> {USD} 100,\newline \;S(30)-{USD} 30,& \mbox{if }{USD} 90\leq S(30)\leq {USD} 100,\newline {USD} 600-6 S(30),&\mbox{if }S(30)< {USD} 90?\end{array}\right. \end{eqnarray*}
Assume that the stock price follows a binomial model with \( n=30 \) steps. The initial price of the stock at time \( 0 \) is \( S_0={USD} 8 \) and in each step the price of the stock goes up by the factor \( u=\frac{5}{2} \) or down by the factor \( d=\frac{2}{5} \). The interest rate is assumed to be \( 0 \). Consider the derived security that pays \( {USD} 1 \) if the price of the stock at time \( n \) is exactly \( {USD} 50 \) and during the time interval \( [0,30] \) the price has reached the level \( B={USD} 125 \) or went above \( B={USD} 125 \). Determine the price of the described security.
Determine the number of sequences \( \left(X_1, X_2, \dots, X_{100}\right) \) with terms in \( \{-1,1\} \) such that \begin{eqnarray*}X_1+X_2+\cdots+ X_{100}=0&&\quad\mbox{and} \newline -32 < X_1+X_2+\cdots+X_k < 18& & \quad \mbox{for each }k\in\{1,2,\dots, 100\}.\end{eqnarray*}