MTH 4300: Practice problems
The user provides integers through the standard input. The first of the numbers is the number k, and is assumed to be non-negative. After this number, the user provides a sequence of non-negative integers, followed by a single negative integer which indicates that the user will not provide any more numbers. Create a program that properly reads the numbers provided by the user, ignores the first k numbers, and among the remaining numbers (if there are any remaining) calculates the sum of those that are odd.
Print the obtained sum to the standard output. If there are no odd numbers to be summed, then the program should print 0.
Example 1:
Input:
8 3 8 5 6 92 84 7 4 2 3 7 2 -9
Output:
10
Explanation: The first number 8, is k. It tells us to ignore the first 8
numbers. Hence we will ignore the numbers 3 8 5 6 92 84 7 4.
Among the remaining numbers, which are 2, 3, 7, 2 we add those that are odd.
Thus we are calculating the sum 3+7=10.
Example 2:
Input:
8 3 8 5 6 92 84 7 4 2 -9
Output:
0
Explanation: The first number 8, is k. It tells us to ignore the first 8
numbers. Hence we will ignore the numbers 3 8 5 6 92 84 7 4.
Among the remaining numbers (and 2 is the only remaining number in this case),
we need to make a sum of those that are odd. Since there is no odd number, the
sum of all odd numbers is 0.
Use recursion to create a program that calculates x[n] if x is a sequence defined as
x[0]=a, x[1]=b, x[n+1]=(x[n]*x[n-1]+x[n-1]+7)%p for n>=1
The user input includes the numbers n, p, a, and b and the program should print x[n] on the standard output.
What happens when the following code is executed? Provide a detailed explanation for your answer.
// fun_with_pointers.cpp
// compile with
// c++ -o f_p fun_with_pointers.cpp -std=c++11
// execute with
// ./f_p
#include<iostream>
int main(){
int *x,*y;
x= new int[5];
y=x;
for(int i=0;i<5;++i){
x[i]=2*i+20;
}
std::cout<<*(y+2)<<std::endl;
delete[] x;
return 0;
}
What happens when the following code is executed? Provide a detailed explanation for your answer.
// abused_pointer.cpp
// compile with
// c++ -o a_p abused_pointer.cpp -std=c++11
// execute with
// ./a_p
#include<iostream>
void pointerAbuse(int *x){
*(x+1)=-2;
}
int main(){
int *x;
x= new int[3];
for(int i=0;i<3;++i){
x[i]=i+5;
}
pointerAbuse(x);
std::cout<<x[0]*x[1]*x[2]<<std::endl;
delete[] x;
return 0;
}
Find the maximal element of a given linked list.
Your code should replace // ??? in the text below in such a way that the obtained c++ source file accomplishes the described task.
// list_maximum.cpp
// compile with
// c++ -o l_max list_maximum.cpp -std=c++11
// execute with
// ./l_max
#include<iostream>
#include"mth4300_list_basics.cpp"
int listMax(ListNode *head){
// ???
}
int main(){
ListNode *head;
head=getListFromTheInput();
std::cout<<listMax(head)<<std::endl;
deleteList(head);
return 0;
}
Two non-empty lists are given with the pointers head1 and head2 to their heads. Create a function
void mergeLists(ListNode *head1, ListNode *head2, const int &location)
that places the list 2 in list 1 after the first occurrence of the number location.
If the list 1 does not contain the number location, then append the list 2 to the end of the list 1.
Example 1: The list1 has content 5,9,2,4,7; the list2 has
the content 6,3,2,6,8; and the value for location is 9. After the application
of mergeLists(head1,head2,location) the list 1 should have the content
5,9,6,3,2,6,8,2,4,7.
Your code should replace // ??? in the text below in such a way that the obtained c++ source file accomplishes the described task.
// merge_lists.cpp
// compile with
// c++ merge_lists.cpp -o merge_l -std=c++11
// execute withfinds a maximal number in the list.
// ./merge_l
#include<iostream>
#include"mth4300_list_basics.cpp"
void mergeLists(ListNode *head1, ListNode *head2, const int &location){
// ???
}
int main(){
ListNode *head1, *head2;
int location;
std::cin>>location;
head1=getListFromTheInput();
head2=getListFromTheInput();
mergeLists(head1,head2,location);
printListToOutput(head1);
deleteList(head1);
return 0;
}
What will be printed on the standard output if the following code is executed? Provide a detailed explanation for your answer.
// classes_move.cpp
// compile with
// c++ -o c_move classes_move.cpp -std=c++11 -fno-elide-constructors
// execute with
// ./c_move
#include<iostream>
class Gandalf{
public:
Gandalf();
Gandalf(const Gandalf &);
Gandalf(Gandalf &&);
void operator=(const Gandalf &);
void operator=(Gandalf &&);
~Gandalf();
};
Gandalf::Gandalf(){
std::cout<<"1";
}
Gandalf::Gandalf(const Gandalf & copyFrom){
std::cout<<"2";
}
Gandalf::Gandalf(Gandalf && moveFrom){
std::cout<<"3";
}
void Gandalf::operator=(const Gandalf & copyFrom){
std::cout<<"4";
}
void Gandalf::operator=(Gandalf&& moveFrom){
std::cout<<"5";
}
Gandalf::~Gandalf(){
std::cout<<"6";
}
Gandalf uselessFunction(Gandalf G){
return G;
}
void gandalfPrints(){
Gandalf G;
std::cout<<"7";
G=uselessFunction(G);
std::cout<<"8";
}
int main(){
gandalfPrints();
std::cout<<std::endl;
return 0;
}
What will be printed on the standard output if the following code is executed? Provide a detailed explanation for your answer.
// strange_recursion.cpp
// compile with
// c++ -o stRec strange_recursion.cpp -std=c++11
// execute with
// ./stRec
#include<iostream>
int strangeRec(int *x){
int result=0;
if(*x>0){
result=*x+strangeRec(x+1);
}
return result;
}
int main(){
int* seq;
seq=new int[6];
seq[0]=8;seq[1]=7;seq[2]=-3;seq[3]=5;seq[4]=-2;seq[5]=12;
std::cout<<strangeRec(seq)<<std::endl;
delete[] seq;
return 0;
}
Given two positive integers n and k and a sequence a[0], a[1], ..., a[k-1] of positive integers, consider the following game played between players A and B that involves a pile of coins. Originally, the pile contains n coins. The player A starts the game and the players alternate the moves. In each move a player must take from the pile either a[0], a[1], ..., or a[k-1] coins. The player who cannot make a move is the loser.
Write a program that takes from the standard input the numbers n, k, and the sequence a[0], a[1], ..., a[k-1] and on the standard output prints the name of the player who has the winning strategy. In addition, if A has the winning strategy, the program should print a number of coins that the player A takes in the first turn.
For given \(n\), find all possible tilings of the \(2\times n\) table with the figures shown in the picture below.

The first figure is the rectangle \(1\times 2\); the second is the rectangle \(2\times 1\); the last figure is obtained by removing a corner from a rectangle \(2\times 2\).
The user input consists of the integer \(n\). The output should be the number of tilings, and in the case that \(n\leq 10\) the output should first list all the tilings. Each tiling is represented as a \(2\times n\) matrix \(A\) whose entry \(A_{ij}\) is one of the numbers \(1\), \(2\), or \(3\), depending on which of the figures (\(1\), \(2\), or \(3\) from above) covers the cell \((i,j)\) of the table.
For example, when \(n=5\), these are some (but not all) of the tilings of the board \(2\times n\):
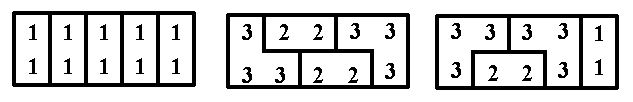
These three tilings should be written on the standard output as
11111 11111 ----- 32233 33223 ----- 33331 32231 -----
Example:
Input:
3
Output:
111 111 --- 122 122 --- 221 221 --- 333 333 --- 333 333 --- 5