MTH4300 Home

MTH 4300: Final Practice 7

Problem 1.

Create program that generates the following sequence \(M\) with a total of 10000 terms:

\[M=\left(\underbrace{\underbrace{9,7,5,-2,3}_{5},\underbrace{9,7,5,-2,3}_{5}, \dots,\underbrace{9,7,5,-2,3}_{5}}_{10000}\right).\] Your code should replace // ??? so that the obtained function 
int* generateSequence(){
  // ???
}
creates the desired sequence when called from the main function with the command 
int* M=generateSequence();

Problem 2.

What happens when the following program is executed? Provide a rigorous justification for your answer. 

// myCode.cpp
 // compile with 
 // c++ myCode.cpp -o myProgam -std=c++11
 // execute with 
 // ./myProgram
 #include<iostream>
class Mountain{
 public:
     int height;
     Mountain();
     Mountain(const Mountain & );
 };
 Mountain::Mountain(){
     height=6;
 }
 Mountain::Mountain(const Mountain & c){
     height=c.height+14;
 }
 int solve(Mountain x){
     return x.height;
 }
 int get(Mountain & x){
     return x.height;
 }
 int main(){
     Mountain lassen; 
     std::cout<<2*solve(lassen) + 10*get(lassen)<<"\n";
     return 0;
}

Problem 3.

Assume that cats and dogs are two objects of the type std::set<int> and that they satisfy \begin{eqnarray*}\mbox{cats} &=&\left\{17,18,19,20,21,22,23,24,25,26,27,28,29,30,31\right\},\newline \mbox{dogs}&=&\left\{29,30,31,32,33,34,35,36,37,38,39,40,41,42,43\right\}. \end{eqnarray*} What is printed on the standard output when the following block of code is executed? 

for(int i=38;i<48;++i){
     if(dogs.find(i)!=dogs.end()){
          cats.insert(i);
     }
 }
 std::cout<<cats.size()<<std::endl;

Problem 4.

How many times is the letter y printed on the standard output when the following program is executed? Provide a rigorous justification for your answer. 

 // myProg.cpp
 // compile with
 // c++ myProg.cpp -o myP -std=c++11 -fno-elide-constructors
 // execute with 
 // ./myP
 #include<iostream>
 class Queen{
 public:
     Queen();
     Queen(const Queen&);
     Queen(Queen&&);
     void operator=(const Queen&);
     void operator=(Queen&&);
     ~Queen();
 };
 Queen::Queen(){
     std::cout<<"y";
 }
 Queen::Queen(const Queen& k){
     std::cout<<"yy";
 }
 Queen::Queen(Queen&& k){
     std::cout<<"yyy";
 }
 void Queen::operator=(const Queen& k){
     std::cout<<"yy";
 }
 void Queen::operator=(Queen&& k){
     std::cout<<"y";
 }
 Queen::~Queen(){
     std::cout<<"y\n";
 }
 Queen slowFun(Queen& k){
     Queen a=k;
     return a;
 }
 int main(){
     Queen k,b;
     b=k;
     for(int i=0;i<5;++i){
          b=slowFun(k);
     }
     return 0;
 }

Problem 5.

The node of the binary tree is defined in the following way

class TN{
 public:
    long content;
    TN* aLeft;
    TN* aRight;
};

The implementation of the function f is given below

long f(TN* a, long h){
    if(a==nullptr){
        return 1;
    }
    long c=a->content;
    return (c%10)+(h%2)*f(a->aLeft,h+1)+(c%2)*f(a->aRight,h+1);
 }

Assume that aRoot is the pointer to the root of the tree

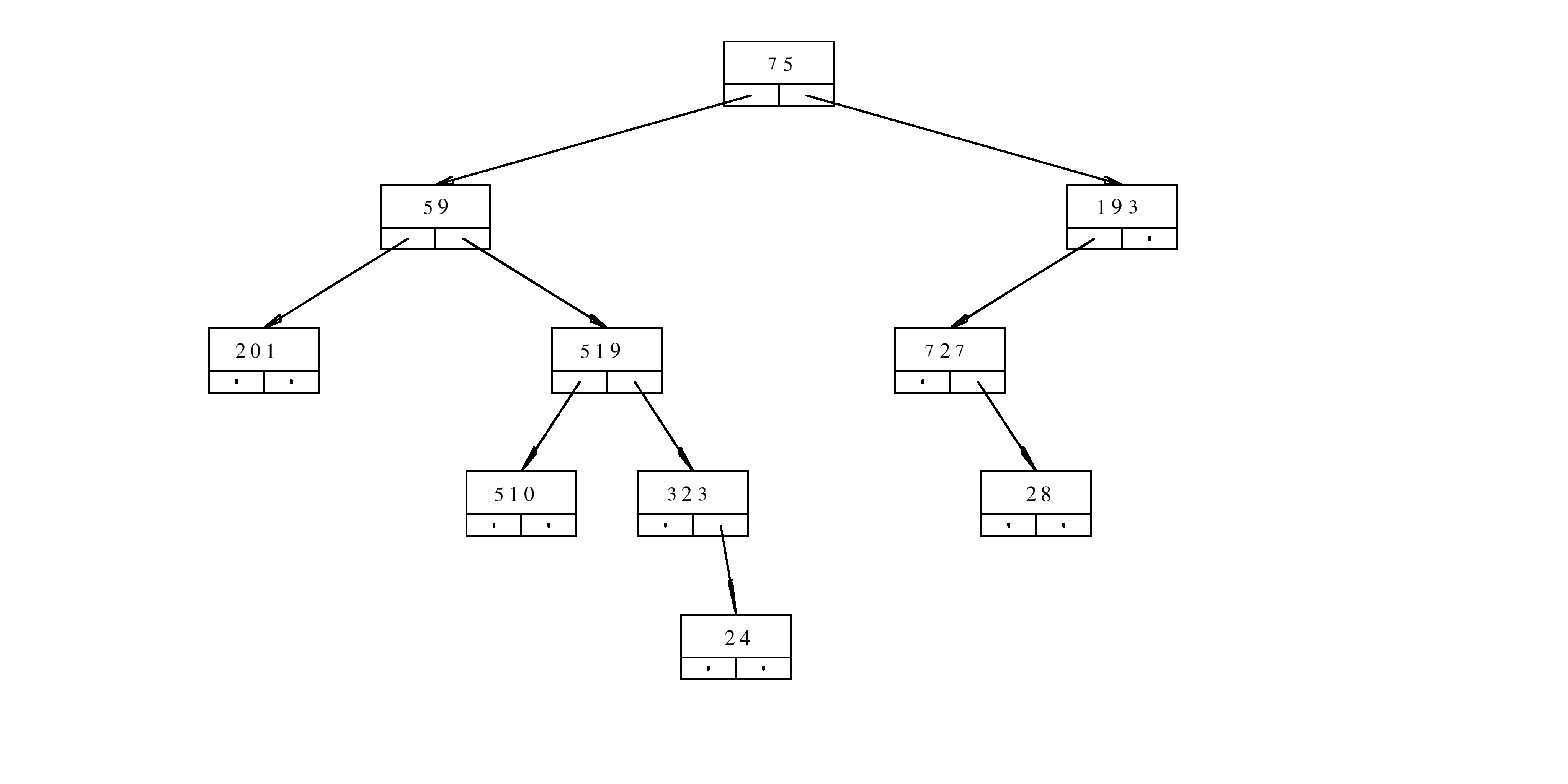
This image provides a visual illustration of content discussed nearby.

What is the result of the evaluation f(aRoot,3)? Provide a rigorous justification for your answer.

Problem 6.

The user input consists of a positive integer \(n\) followed by a sequence of \(n\) integers \(x_0\), \(x_1\), \(\dots\), \(x_{n-1}\). Create the program that calculates the total number of different outcomes that can be obtained as the results of the expressions \[\pm x_0\pm x_1\pm x_2\pm\cdots\pm x_{n-1}\] for all choices of signs \(+\) and \(-\).

Example :

Input:
 3 
5 5 -5 
 Output:
 4

Explanation: There are \(4\) possible results. They are \(-15\), \(-5\), \(5\), and \(15\) and can be obtained in the following way: \begin{eqnarray*} -15&=&-x_0-x_1+x_2\newline -5&=& -x_0+x_1+x_2=+x_0-x_1+x_2=-x_0-x_1-x_2\newline 5&=&+x_0-x_1-x_2=-x_0+x_1-x_2=+x_0+x_1+x_2\newline 15&=&+x_0+x_1-x_2. \end{eqnarray*}