MTH 4300: Final Practice 6
15, 17, 19, 22, and 24, then prints all the numbers in this linked list, and then deletes the list and prevents memory leak.
R is given below
class R{
private:
int m;
public:
int n;
void setM(int );
void setN(int );
int getM();
getN();
};
void R::setM(int vvv){m=vvv;}
void R::setN(int vvv){n=vvv;}
int R::getM(){return m;}
int R::getN(){return n;}
Which of the following lines must not appear in the main() function of a program?
(A)
R r; r.setN(37); (B) R r; r.setN(r.m+37); (C) R r; r.setM(37); (D) R r; r.n=37; (E) R r; r.setM(r.n+37);
(A) \(11.256\) (B) \(12.27\) (C) \(14.125\) (D) \(16.1\) (E) \(17.2\) (F) \(18.14\) (G) \(20.95\)
Consider the following AVL tree.
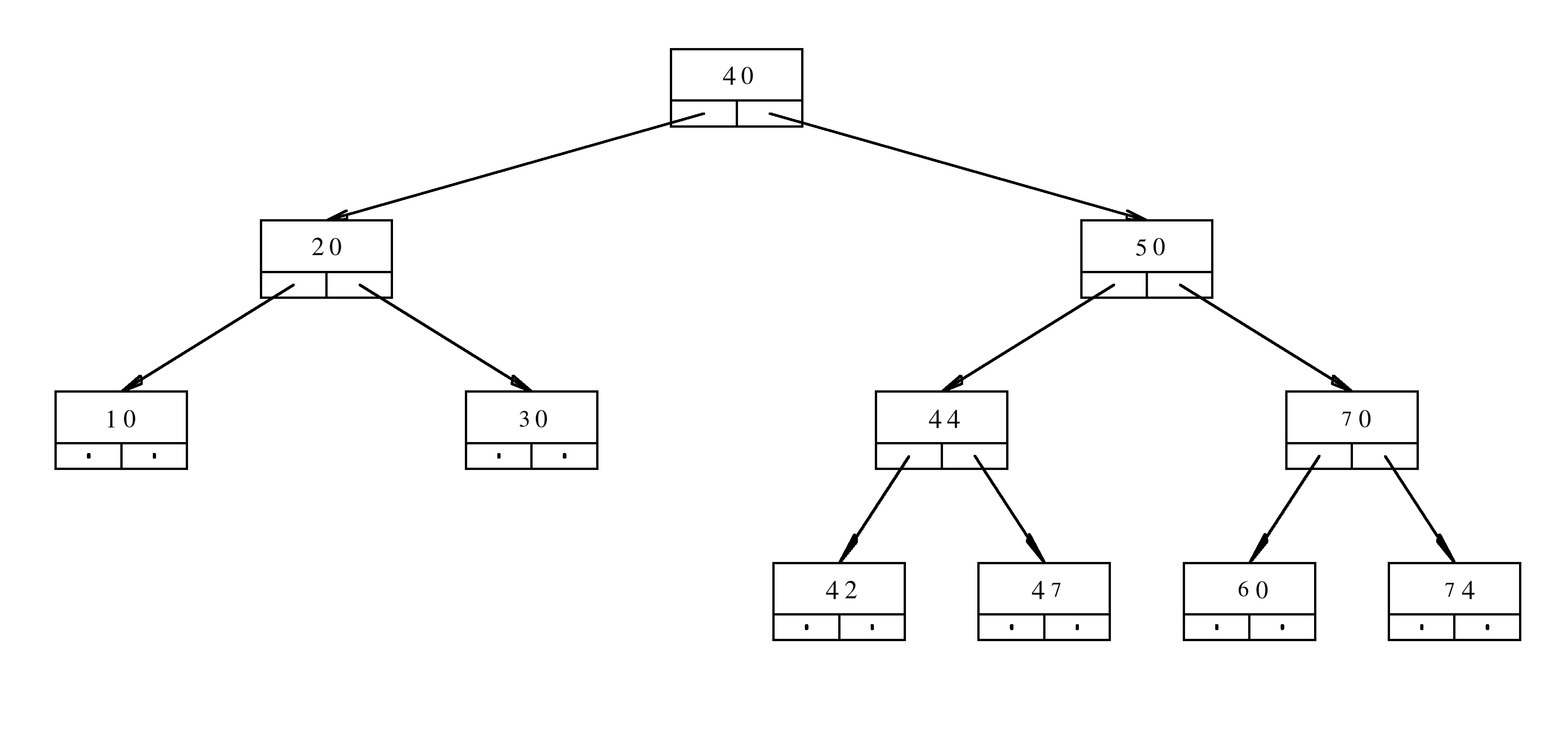
Determine a positive integer \(x\) that satisies the following condition: If \(x\) is inserted into the given AVL tree, then exactly one "double rotation" must be applied to maintain the AVL structure.
Remark: There could be more than one such \(x\). You need to determine one of them and explain why it has the desired property.
The user input consists of a positive integer \(n\), \(n\) pairs of strings and real numbers, and an integer \(k\) from the set \(\{1\), \(2\), \(\dots\), \(n\}\). For each \(i\in\{0\), \(1\), \(\dots\), \(n-1\}\), the first component of the pair is the string horse[i] that represents the name of a horse. The second component time[i] is of type double and represents the time it took the horse horse[i] to complete the race. Create the program that prints the name of the horse who finished the race at the position \(k\). If there are ties, the program is allowed to print the name of any of the horses who arrived in the group that contains the \(k\)-th place. All horses have different names.
Example:
Input: 6 Darcy 17.211 Chug 15.288 Suki 8.37 Avi 12.8 Dax 14.2 Teddy 19.82 3 Output: Dax
Explanation: The number \(n\) and \(k\) are the first and the last. Hence, \(n=6\) and \(k=3\). The fastest horse is Suki with time \(8.37\). The next one is Avi with time \(12.8\). The horse at position \(3\), i.e. the third horse, is Dax with time \(14.2\), hence the program should print Dax.
The user input consists of two positive integers \(x\) and \(y\) of type long such that neither \(x\) nor \(y\) contains the digit \(0\) in their decimal expansion. Create a program that determines whether the number \(y\) can be obtained by rearranging the digits of the number \(x\).
Example 1:
Input: 353771 517373 Output: Yes
Example 2:
Input: 3544 3543 Output: No