MTH 4300: Final Practice 1
Create the class Mountain with two private attributes: The attribute name has to be of type std::string and the attribute height has to be of type double. Create the public methods that can be used to set the values to the attributes and to read the values from the attributes.
Write a program that reads a positive integer n from the user input and properly allocates the memory for a sequence sM of n objects of class Mountain using the operator new. The program should then receive n pairs of strings and numbers from std::cin and store these values in the sequence sM. The program should then read a positive real number r and print all terms of the sequence sM whose attribute height is smaller than r.
Assume that we have a supercomputer and that the type bigInt can store all integers smaller than \(10^{1000}\).
The class Elephant has public attributes alpha, beta, and gamma of type bigInt. Assume that the class Elephant has a properly implemented comparison operator operator< and that std::set<Elephant> can be used in programs.
The declaration of the class Bird and the implementation of its methods are given below
class Bird{
private:
bigInt num;
public:
Bird();
Bird(const Elephant& );
Bird(std::set<Elephant>::const_iterator );
bigInt getNum() const;
};
Bird::Bird(){num=0;}
Bird::Bird(const Elephant& abc){
num=0;
if (( abc.alpha < 700) && (abc.beta < 700) && (abc.gamma < 700) ){ num=3; }
}
Bird::Bird(std::set<Elephant>::const_iterator abc){
num=0;
if (( abc->alpha < 3500) && (abc->beta < 3500) && (abc->gamma < 3500) ){ num=8; }
}
bigInt Bird::getNum() const{return num;}
It is known that the variables first and second are of type std::set<Elephant>. The set first contains all possible objects of type Elephant whose components alpha, beta, and gamma are non-negative integers divisible by \(5\) and smaller than \(10^{1000}\). The set second contains all possible objects whose components alpha, beta, and gamma are non-negative integers divisible by \(7\) and smaller than \(10^{1000}\).
What is the value of sing(first,second), where the function sing is implemented below? Provide a rigorous justification for your answer.
bigInt sing(const std::set<Elephant>& a, const std::set<Elephant>& b){
bigInt res=0;
std::set<Elephant>::const_iterator i;
i=a.begin();
while(i!=a.end()){
if(b.find(*i)!=b.end()){
Bird temp(*i);
res += temp.getNum();
}
++i;
}
return res;
}
The objects of the class SN are nodes of a stack. The components are real numbers of type double.
The function stackOperations is implemented below, but it is missing one line of code. The word MISSING_LINE is placed instead of that line. The function has to reverse the order of the elements in the stack a2 and move them to the top of the stack a1.
SN* stackOperations(SN* a1, SN* a2){
SN* nTop;
nTop=a1; SN* runner=a2;
while(runner!=nullptr){
nTop=push(nTop,runner->content); runner=runner->aNext;
}
MISSING_LINE
return nTop;
}
The call of the function inside main() would be made with the following code
SN* aNewStack=stackOperations(aTop1,aTop2);
You can assume that before the call, the pointers aTop1 and aTop2 contain the addresses of the top terms of two properly created stacks. After the call, the stack that was originally pointed at by aTop2 should be empty and its terms placed on top of the first stack.
Which of the following commands should be placed instead of MISSING_LINE to prevent the function from producing a memory leak?
- (A)
delete runner->aNext; - (B)
delete a2; - (C)
delete[] runner; - (D)
while(a2!=nullptr){a2=pop(a2);} - (E)
delete[] a2; - (F)
delete a1; - (G) The text
MISSING_LINEshould be erased and no command should be put instead of it. The code does not produce memory leaks. - (H)
delete[] a1;
Create a program that counts the total number of recipes that are provided by the user. User input consists of multiple lines. Each line starts with an integer \(n\). If \(n\) is negative, then this is the signal that the input is over. If \(n\) is positive, then \(n\) is the number of ingredients in the recipe. After the number \(n\), the line consists of \(n\) different strings that represent the names of the ingredients.
Two recipes are considered the same if they have the same ingredients. For example, these two recipes are the same
3 strawberry chocolate banana 3 chocolate banana strawberryExample
Input 3 strawberry chocolate banana 2 chocolate strawberry 2 chocolate banana 3 chocolate banana strawberry 2 strawberry chocolateThe corresponding output should be
3.
The declaration of the class whose objects are nodes of a tree is
class TN{
public:
long content;
TN* aLeft;
TN* aRight;
};
The tree is damaged. The leaves that should contain the null pointers are now pointing to some other nodes. The picture of this damaged tree is shown below.
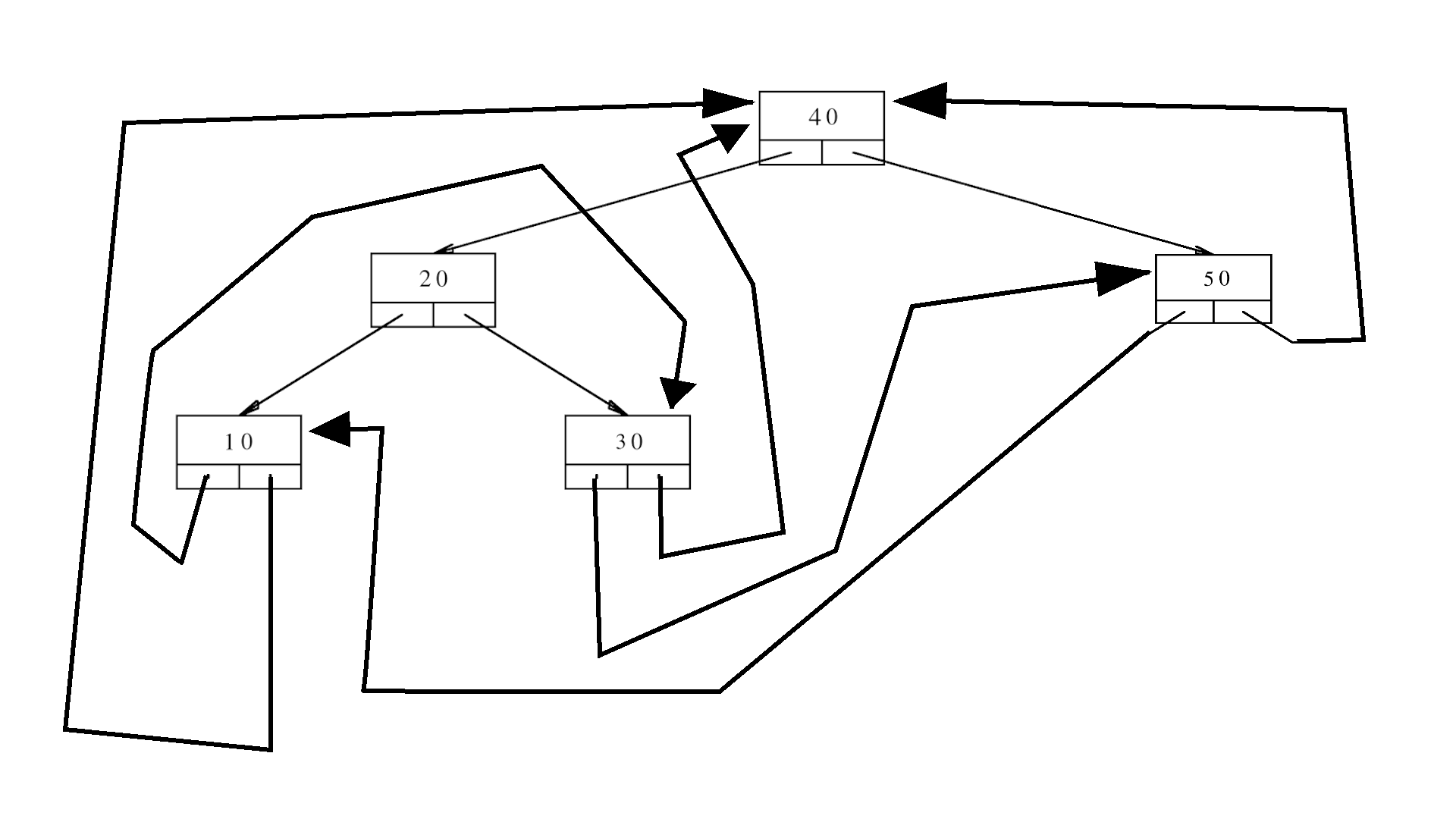
The implementation of the functions f and g are given below
long f(TN* t){
t=t->aLeft;
t->content += 1;
return t->content;
}
long g(TN*& t){
t=t->aRight;
t->content += 2;
return t->content;
}
The pointer aHead initially contains the address of the root of the tree (the root contains the number \(40\)). What is the output of the following code? Provide a rigorous justification for your answer.
aHead=aHead->aLeft;long sum=0;
for(long i=0;i<3;++i){
sum+=f(aHead); sum+=g(aHead);
}
std::cout<<sum<<"\n";
Your program should use data structures based on binary search trees to achieve the polynomial complexity.
Example: \(m=10\), \(n=6\); The fees at the airports \((3,0)\), \((7,0)\), \((9,2)\) are 5; The fees at the airports \((3,3)\) and \((3,4)\) are \(1\); The fees at all other airports are \(800\). Then the cheapest flight has the cost \(815\). The path is \((0,0) \to (3,0) \to (7,0) \to (9,2) \to (10,6)\).