MTH 4150: Midterm 1 Practice 3
Let \( A=\{1,2,3,4,5\} \) and \( B=\{7,5\} \).
- (a) Provide an example of a function \( f:A\to B \) that is onto.
- (b) Provide an example of a function \( g:A\to B \) that is not onto.
- (c) Determine the total number of onto functions whose domain is \( A \) and codomain is \( B \).
A box contains \( 70 \) marbles with labels \( \{1 \), \( 2 \), \( \dots \), \( 70\} \). What is the smallest number of marbles that a blindfolded person must take from the box to guarantee that two of the marbles taken have labels whose difference is divisible by \( 18 \)?
The sequence \( (a_n)_{n=1}^{\infty} \) satisfies \( a_1=4 \), \( a_2=28 \), and \[ a_{n+2}=4a_{n+1}+12a_{n},\quad\mbox{for } n\geq 1.\] Prove that the following formula holds for every \( n\geq 1 \) \[ a_n=\frac{6^{n+1}-(-2)^{n+1}}{8}.\]
A sequence whose all terms are from \[ S=\{ A,B,C,D, E,F,G,H,I,J,K,L,M,N,O,P\}\] is called honorable if each letter from \( \{E,F,G,H,I,J,K,L,M,N,O,P\} \) is followed by the letter \( A \). For example, the sequences \( (B,B,G,A,B) \) and \( (B,B,G,A,B) \) are honorable, while \( (B,G,B,B,B) \) and \( (B,B,A,B,G) \) are not. Determine the formula for the number of honorable sequences of length \( n \).
Find the number of sequences \( \left(a_1,a_2,a_3,a_4\right) \) of integers such that \[ a_1\geq 0,\; a_2\geq a_1+5,\; a_3\geq a_2+9,\; a_4\geq a_3+4,\; a_4\leq 32.\]
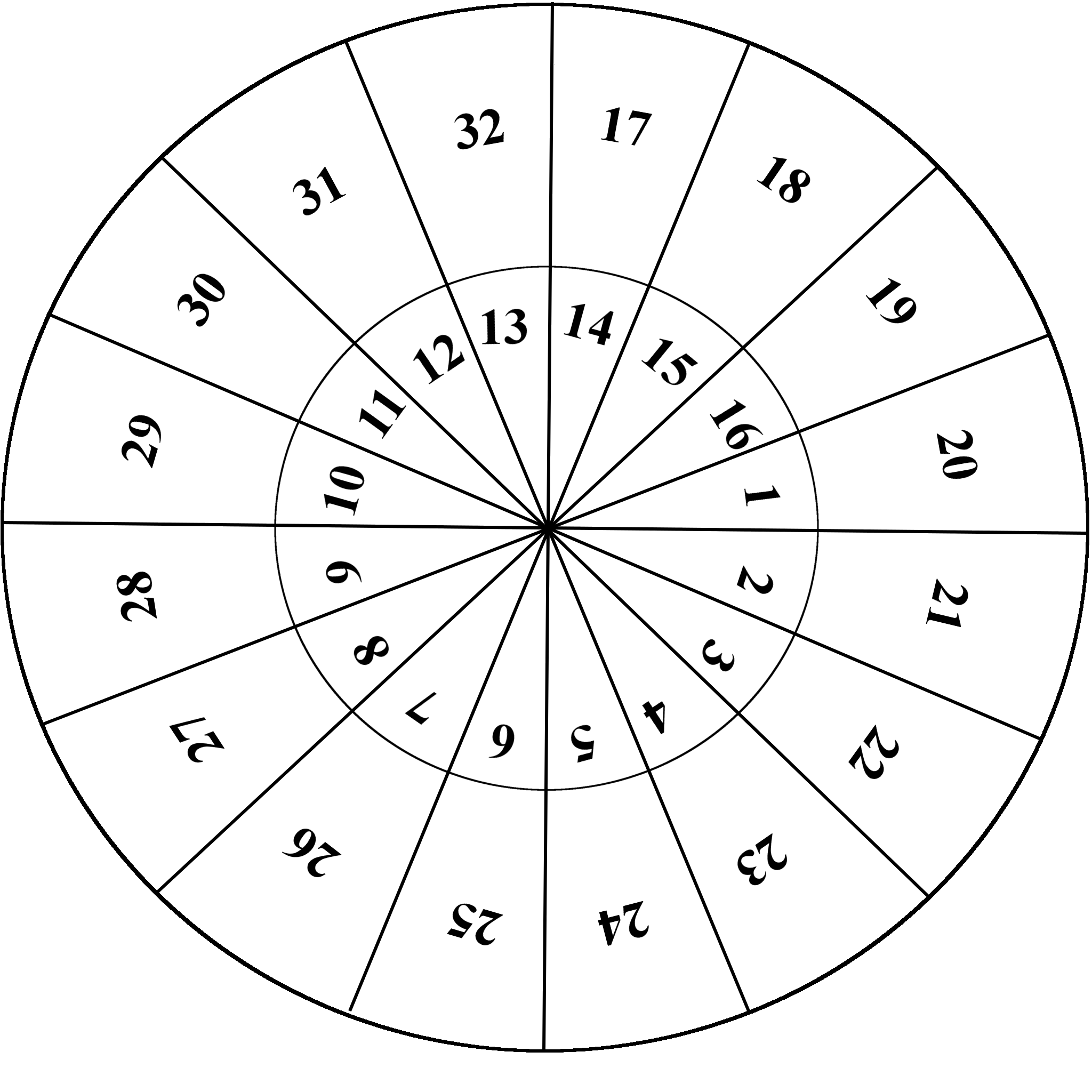
Two circles with the same center are cut into \( 16 \) equal sectors and the sectors are labeled as shown in the picture to the left. The inner circle can rotate, and the entire system can have 16 different configurations. For example, one of the configurations is shown in the picture to the right and is obtained when the inner circle rotates clockwise by \( 3 \) sectors (each sector is \( 22.5^{\circ} \) and the entire rotation is for an angle of \( 67.5^{\circ} \)).
Bart and Lisa start with \( 16 \) dollars each and play the following game that has three steps:
- Step 1. Lisa pays \( 7 \) dollars to Bart.
- Step 2. Bart chooses \( 8 \) of the outer sectors and \( 8 \) of the inner sectors and paints them in green. Then he paints the remaining \( 8 \) outer sectors and remaining \( 8 \) inner sectors in red.
- Step 3. Lisa rotates the inner circle so that the inner sectors align with the outer sectors. For each pair of sectors with matching colors, Bart has to give \( 1 \) dollar to Lisa.
The winner is the player who gets more money. Who has the winning strategy: Bart or Lisa? Provide a rigorous justification for your answer.
 \(\quad\quad\quad\)
\(\quad\quad\quad\)