MTH 4150: Midterm 1 Practice 1
In how many different ways we can assign offices to two employees if the total number of offices in the company is \(100\)?
How many different bit strings of length \(20\) are there?
How many one-to-one functions are there from a set with \(m\) elements to one with \(n\) elements?
Determine the number of positive integers whose decimal expansion contains exactly 4 digits, but does not contain equal digits, and does not contain the digit \(3\).
How many bit strings of length eight start with \(1\) or end with the two bits \(00\)?
How many integers between \(1\) and \(1000\) have all their digits different and do not contain the digit \(5\) in their decimal expansion?
Let \(S\) be a subset of the set \(\{1,2,3,\dots, 2n\}\). Assume that the equation \(x+y=2n+1\) does not have solutions in \(S\) (i.e., if \(x,y\in S\), then \(x+y\neq 2n+1\)). What is the largest number of elements that \(S\) can have?
Let \(n\geq 1\) be a positive integer. If \(a_1, \dots, a_n\) are positive integers, prove that it is possible to paint some of these numbers in green in such a way that the sum of green numbers is divisible by \(n\).
In how many ways can we distribute 15 identical apples to 4 distinct students? Not all students have to get an apple.
Determine the total number of triples of nonnegative integers \((a,b,c)\) that satisfy \[a+b+c=30.\]
In how many different ways can we give 5 identical apples to 20 different students so that no student gets all 5 apples? (All apples are supposed to be given to students).
In how many different ways can we distribute \(15\) identical apples to \(4\) different students if not all of the apples have to be distributed?
Determine the number of subsets of \(\{1, 2, 3, 4, \dots, 50\}\) whose sum of elements is larger than or equal to 638.
Let \(n > 3\) be an integer. \(n\) teams participated in a basketball tournament. Each team played one game with every other team. There were no ties. Prove that there exists a team \(A\) such that: For every team \(B\) that won a game against \(A\), there exists a team \(C\) such that \(A\) won the game against \(C\), and \(C\) won the game against \(B\).
Each of three schools contain \(n\) students. Each student has at least \(n+1\) friends among students of the other two schools. Prove that there are three students, all from different schools who are friends to each other. (Friendship is symmetric: If \(X\) is a friend to \(Y\), then \(Y\) is a friend to \(X\).)
A corner square is removed from the \(8\times 8\) chessboard. Can the rest be tiled by \(1\times 3\) rectangles?
- (a) Is it possible to tile the \(8\times 8\) board using the figures
congruent to
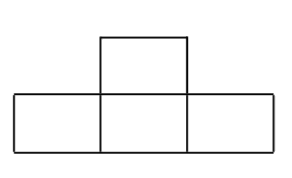 ?
?
- (b)
Is it possible to tile the \(10\times 10\) board using the figures
congruent to
 ?
?
