MTH4140: Midterm 2 Practice 2
Provide an example of a graph whose chromatic number is 5
Construct an example of a simple graph \(G\) that has \(6\) vertices and \(9\) edges. Determine \(\omega(G)\) of the graph \(G\) that you constructed.
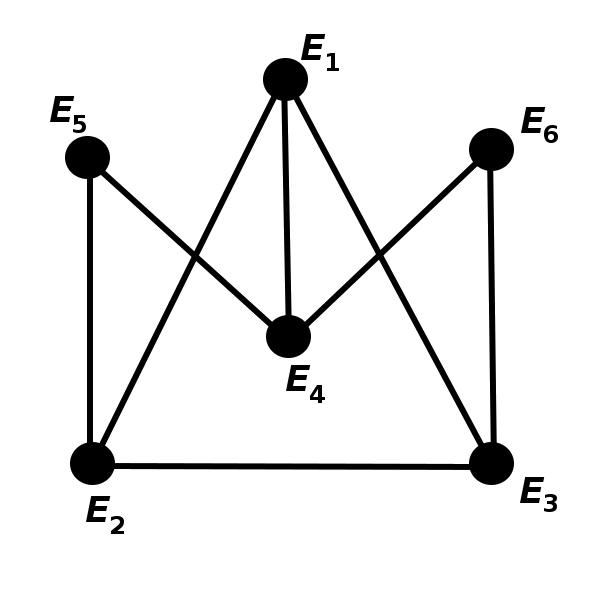
Determine the chromatic polynomial of the graph below
Assume that the chromatic number of the simple graph \(H\) is equal to \(k\) and that \(H\) is a \(k\)-critical graph. Prove that the following inequality holds \[\delta(H)\geq k-1,\] where \(\delta(H)\) is the minimum of the degrees of vertices in \(H\).
Assume that a simple graph \( G \) has exactly \( 52 \) vertices and the set of vertices has three disjoint subsets \( T_1 \), \( T_2 \), and \( T_3 \) that satisfy the following two properties:
- (i) Each of the subsets \( T_1 \), \( T_2 \), and \( T_3 \) has \( 5 \) vertices;
- (ii) For each \( i\in\{1,2,3\} \) no two vertices of \( T_i \) are adjacent.
Prove that \( \chi(G)\leq 40 \).