MTH4140: Midterm 2 Practice 1

Assume that \(k\) is a given positive integer. Consider the graph \(G=(V,E)\), where \(V=\left\{A, B_1, B_2, \dots, B_{k+2}\right\}\) and \[E=\left\{(A,B_i), (B_i,A): i\in\{1,2,\dots, k+2\right\}.\] Then the degree of the vertex \(A\) is \(k+2\) and the degree of every other vertex is \(1\). Therefore \(\Delta(G)-k=2\). The graph can be colored in \(2\) colors: \(A\) is green and every other vertex is red. Clearly, the graph cannot be colored in fewer than \(2\) colors since it is connected.

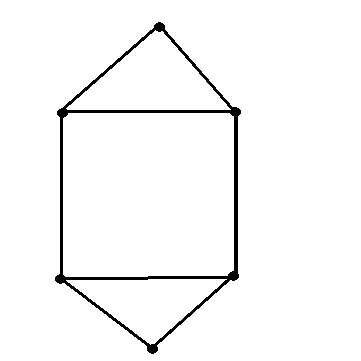
Let us label the vertices of the graph with \(A\), \(B\), \(C\), \(D\), \(E\), and \(F\). The iner square is \(ABCD\), while \(E\) and \(F\) are two vertices such that \(E\) is connected to \(A\) and \(B\) and \(F\) is connected to \(C\) and \(D\).

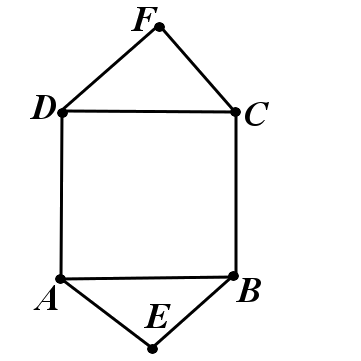
Let us denote by \(S\) the set of all colorings of \(G\) in \(x\) colors. Denote by \(S_{1}\) the set of those colorings in which \(A\) and \(C\) are of the same color, and \(S_{2}\) the set of colorings in which \(A\) and \(C\) are of different colors. We will first find the number of elements in \(|S_1|\). There are \(x\) possibilities for \(A\) and \(C\). Then there are \(x-1\) possibilities for each of \(B\) and \(D\), and \(x-2\) for each of \(E\) and \(F\). Hence \(|S_1|=x(x-1)^2(x-2)^2\).

If \(A\) and \(C\) are of different colors, there are \(x(x-1)\) ways to color two of them. Then each of \(B\) and \(D\) can be in one of \(x-2\) colors. Once \(A\) and \(B\) are painted, there are \(x-2\) options for \(E\), and once \(C\) and \(D\) are painted there are \(x-2\) options for \(F\). Hence \(|S_2|=x(x-1)(x-2)^4\). Therefore we have \begin{eqnarray*} P_G(x)&=&|S_1|+|S_2|=x(x-1)(x-2)^2\left((x-1)+(x-2)^2\right) \newline &=&x(x-1)(x-2)^2\left(x^2-3x+3\right). \end{eqnarray*}

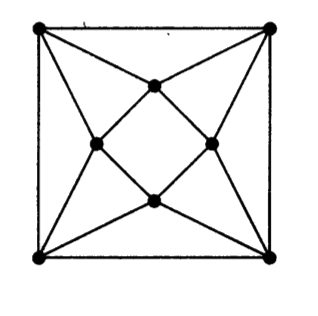
We will prove that \(\chi(\mathcal G)=4\). We will identify a \(4\)-critical subraph of \(\mathcal G\) by \begin{eqnarray*} \mathcal G^{\prime}&=&\left(V^{\prime},E^{\prime}\right), \mbox{ where } V^{\prime}=\left\{A, B, C, D, E, F, G\right\} \mbox{ and}\newline E^{\prime}&=&\left\{(A,B), (B,A),(A,C), (C,A), (B,C), (C,B), (A,D), (D,A), (C,D), (D,C),\right.\newline &&\left. (D,G), (G,D), (B,E), (E,B), (B,F),(F,B), (E,F),(F,E), (E,G),(G,E),(G,F),(F,G)\right\}. \end{eqnarray*}

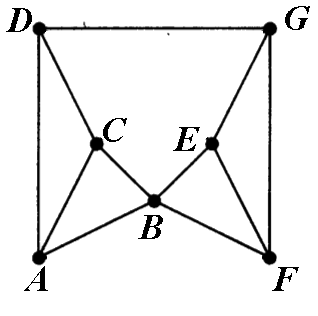
It is sufficient to prove that \(\chi(\mathcal G)= 4\) and that by erasing any edge of \(\mathcal G^{\prime}\) we obtain a graph that can be colored in \(3\) colors.

Consider the center of symmetry of the geometrical representation of the graph \(\mathcal G\). There are four pair of vertices that are centrally symmetric. Each pair can be colored with the same color. Therefore \(\chi(\mathcal G)\leq 4\). We will now prove that \(\chi\left(\mathcal G^{\prime}\right)\geq 4\) by proving that it is impossible to color \(\mathcal G^{\prime}\) in \(3\) colors. Assume the contrary, that we can color \(\{A,B,C,D,E,F,G\}\) in three colors. Then all three colors must be used on the subgraph generated by \(\{A,B,C\}\), since that subgraph is a complete graph of size \(3\). Similarly, all three colors must be used on \(\{A,C,D\}\), hence \(B\) and \(D\) must be of the same color. The same argument proves that \(B\) and \(G\) must be of the same colors which allows us to conclude that \(D\) and \(G\) are of the same color and that is not possible since \(D\) and \(G\) are neighbors. Thus \(\chi(\mathcal G)=4\) and \(\chi\left(\mathcal G^{\prime}\right)=4\).

We will now prove that if we erase any edge of \(\mathcal G^{\prime}\) the obtained graph can be colored in \(3\) colors. Let us consider the following cases:

• Case 1. The edge \((D,G)\) is removed from \(\mathcal G^{\prime}\). Then we can paint \(D\), \(G\), and \(B\) in color \(1\); \(A\) and \(F\) in color \(2\); and \(C\) and \(E\) in color \(3\);

• Case 2. One of the edges \((A,D)\) or \((F,G)\) is erased from \(\mathcal G^{\prime}\). Due to symmetry we may assume, without loss of generality, that \((F,G)\) is erased. Then we can color \(G\), \(F\), and \(C\) in color \(1\); \(B\) and \(D\) in color \(2\), and \(A\) and \(E\) in color \(3\);

• Case 3. One of the edges \((A,C)\) or \((E,F)\) is erased from \(\mathcal G^{\prime}\). Without loss of generality, assume that \((E,F)\) is erased. Then we can color \(E\), \(F\), and \(C\) in color \(1\); \(B\) and \(D\) in color \(2\); and \(A\) and \(G\) in color \(3\);

• Case 4. One of the edges \((C,D)\) or \((E,G)\) is erased from \(\mathcal G^{\prime}\). Without loss of generality, assume that \((E,G)\) is erased. Then we can color \(E\), \(G\), and \(C\) in color \(1\); \(B\) and \(D\) in color \(2\); and \(A\) and \(F\) in color \(3\);

• Case 5. One of the edges \((A,B)\) or \((B,F)\) is erased from \(\mathcal G^{\prime}\). Without loss of generality, assume that \((B,F)\) is erased. Then we can color \(B\), \(F\), and \(D\) in color \(1\); \(C\) and \(E\) in color \(2\); and \(A\) and \(G\) in color \(3\);

• Case 6. One of the edges \((B,C)\) or \((B,E)\) is erased from \(\mathcal G^{\prime}\). Without loss of generality, assume that \((B,E)\) is erased. Then we can color \(B\), \(E\), and \(D\) in color \(1\); \(A\) and \(F\) in color \(2\); and \(C\) and \(G\) in color \(3\);

We have proved that no matter which edge of \(\mathcal G^{\prime}\) is erased, the resulting graph can be colored in \(3\) colors. Thus \(\mathcal G^{\prime}\) is \(4\)-critical.

If \(n=1\) or \(n=2\), the chromatic number is \(1\). For \(n\geq 3\), the chromatic number is \(\lceil \frac{n}3\rceil +1\), where \(\lceil x\rceil\) is the smallest integer not smaller than \(x\). Let \(C_i\) for \(i\in\{0,1,2\}\) be the subset of \(V_n\) consisting of those integers that are congruent to \(i\) modulo \(3\). The subgraph generated by \(C_1\cup \{3\}\) is complete, hence the chromatic number of \(G_n\) is greater than or equal to \(|C_1\cup \{3\}| =\lceil\frac n3\rceil+1\). The vertices of \(G_n\) can be colored in \(\lceil \frac n3\rceil +1\) colors in such a way that no two connected vertices share a color. This can be done by coloring \(C_1\) and \(C_2\) in \(\lceil n/3\rceil\) colors, and coloring all vertices in \(C_0\) in the remaining color.

We will prove that the statement holds for every \(n\geq3\). Clearly, \(\chi(G)\geq\omega(G)\). One graph for which \(\chi(G)=3\) is a cycle of length 5. Assume that for \(n\in\mathbb N\) there is a graph without cycles of length \(3\) such that \(\chi(G)=n\). We want to build a graph \(G^{\prime}\) that does not have cycles of length \(3\) for which \(\chi(G^{\prime})=n+1\). Let \(G=G(V,E)\). Let \(V_n=V\times\{1,2,\dots, n\}\), and \(E_n=\left\{((a,i),(b,i)): (a,b)\in E, i\in\{1,2,\dots, n\}\right\}\). Then \((V_n,E_n)\) is essentially \(n\) discjoint copies of the graph \(G\). We build \(G^{\prime}\) in the following way: \(G^{\prime}=(V^{\prime},E^{\prime})\), where \(V^{\prime}=V_n\cup V^n\), and \(E^{\prime}=E_n\cup E^{\prime\prime}\). We now define \(E^{\prime\prime}\) as the set of edges originating from vertices \(V^n\). Each \((v_1, \dots, v_n)\in V^n\) is connected to all of \((v_1,1)\), \((v_2,2)\), \(\dots\), \((v_n,n)\). Let us prove that \(\chi(G^{\prime}) > n\). Clearly, \(\chi(G^{\prime})\geq n\). Assume that \(\chi(G^{\prime})=n\). Consider one coloring of \(G^{\prime}\) with \(n\) colors. Since each of the subgraphs generated by \(V\times\{i\}\) is isomorphic to \(G\), each of the colors appears in \(V\times \{i\}\). Hence in graph \(V\times\{1\}\) there is a vertex of color \(1\). Assume it is \((a_1,1)\). Similarly, in graph \(V\times\{2\}\) there is a vertex of color \(2\). Denote it by \((a_2,2)\). In graph \(V\times\{i\}\) there is a vertex of color \(i\), and denote it by \((a_i,i)\). Then the vertex \((a_1,a_2,\dots,a_n)\) is connected to each of \((a_i,i)\) and it must share the same color with at least one of them. Contradiction.

It is possible to color \(G\) with \(n+1\) colors. We apply the same proper coloring of \(G\) with colors \(\{1\), \(2\), \(\dots\), \(n\}\) to each of the subgraphs \((V_n,E_n)\). Each of the vertices of \(V^n\) should be colored in \(n+1\). It is clear that the obtained coloring is proper.