MTH4140: Midterm 1 Practice 3
Which of the following statements are true?
- (A) If \( R \) is a relation on \( A \), then \( R\times R = A\times A\times A\times A \).
- (B) A transitive relation on the set \( S \) must be a subset of \( S\times S \).
- (C) If \( f:A\to A \) is a function then the set \( V=\left\{\left(x,f(x)\right):x\in A\right\} \) is a relation on \( A \).
- (D) If \( P \) is a reflexive relation on \( Q \) then \( Q \) is a symmetric relation on \( P \).
- (E) If \( P \) is a relation on \( Q \) then \( P\times Q \) is also a relation on \( Q \).
Provide an example of a set \( S \) of \( 3 \) elements and a function \( f:S\times S\to S \) that is not surjective.
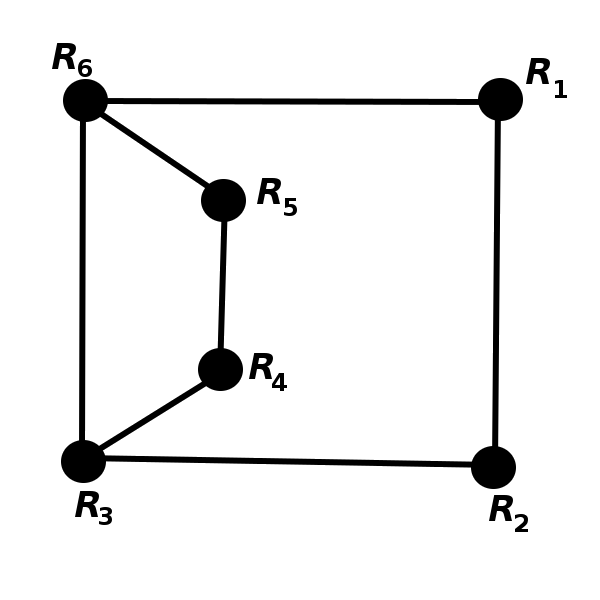
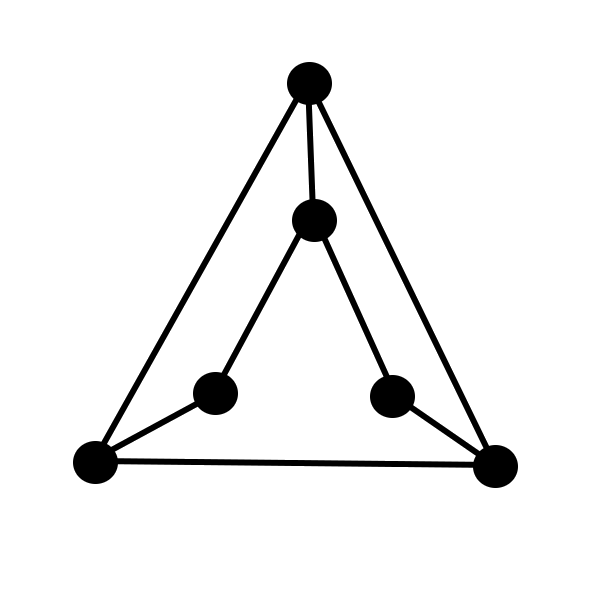
Determine which pairs of graphs below are isomorphic.
 \(\quad\)
\(\quad\)
 \(\quad\)
\(\quad\)
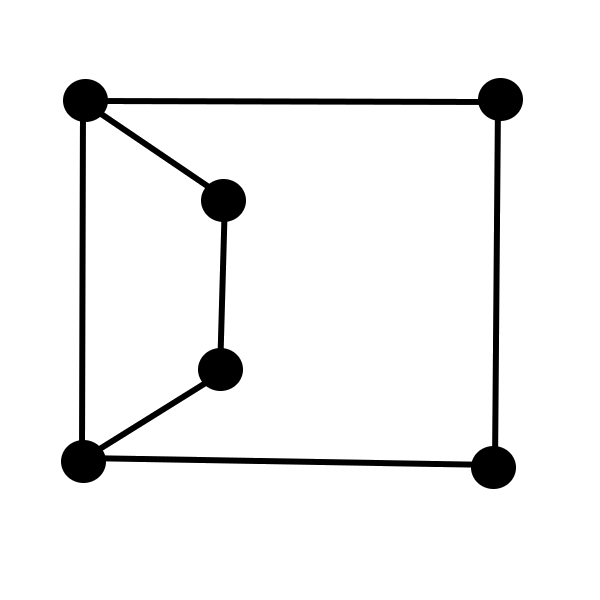
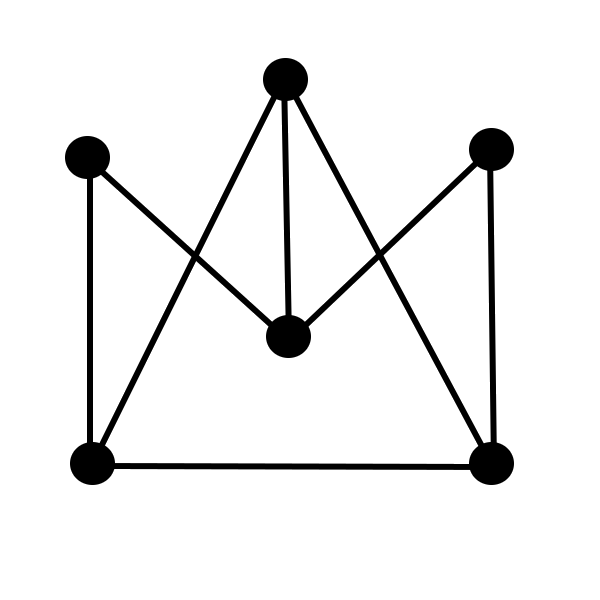
Which of the pictures below can be drawn without lifting the pen from the paper and without tracing the same line twice?
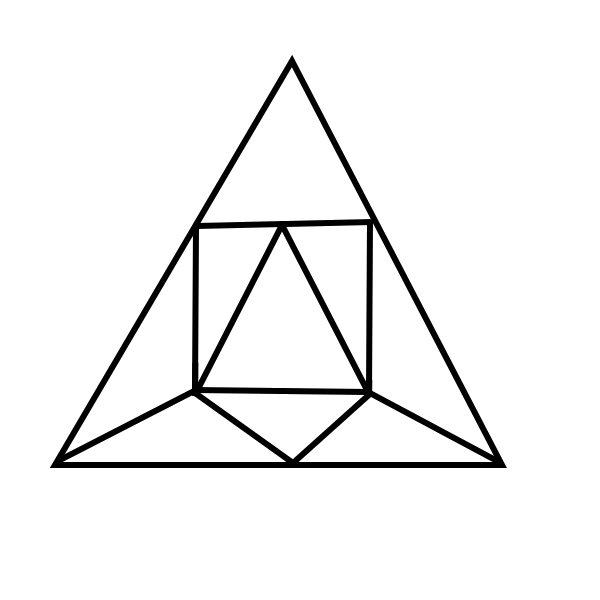 \(\quad\)
\(\quad\)
 \(\quad\)
\(\quad\)
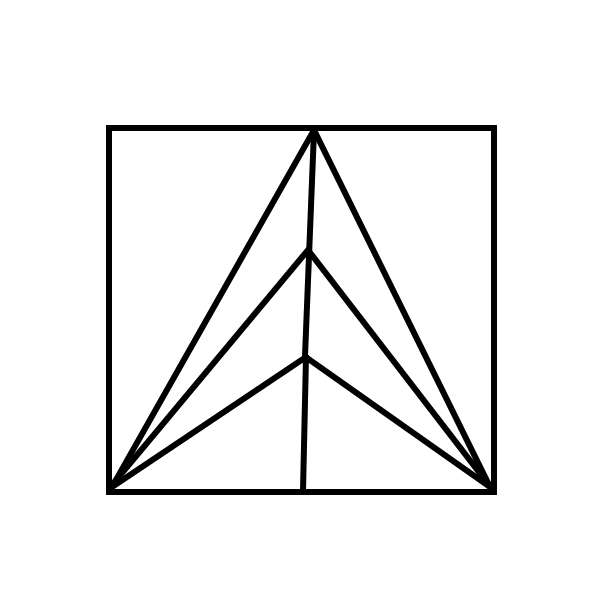
A sequence of integers \( \left(a_n\right)_{n=1}^{\infty} \) satisfies \( a_1=6 \), \( a_2=20 \), and \( a_{n+2}=2a_{n+1}+8a_n \) for \( n\geq 1 \). Prove that \[ a_n=\frac{4 \cdot 4^n-{ } \left(-2\right)^n }{3} \quad\mbox{ for every } n\geq 1.\]
Assume that the set \( V \) is defined as \( V =\left\{ 1,2,\dots, 43 \right\}^{6} \). Assume that \( E \) is the set of all pairs \( (u,v) \) such that \( u=\left(a_1, \dots, a_{6}\right) \) and \( v=\left(b_1,b_2, \dots, b_{6}\right) \) are elements of \( V \) for which the number \( \left(a_1-b_1\right)\cdot\left(a_2-b_2\right) \cdots \left(a_{6}-b_{6}\right) \) is not divisible by \( 7 \). Determine whether the graph \( (V,E) \) has a path that visits every edge exactly once.
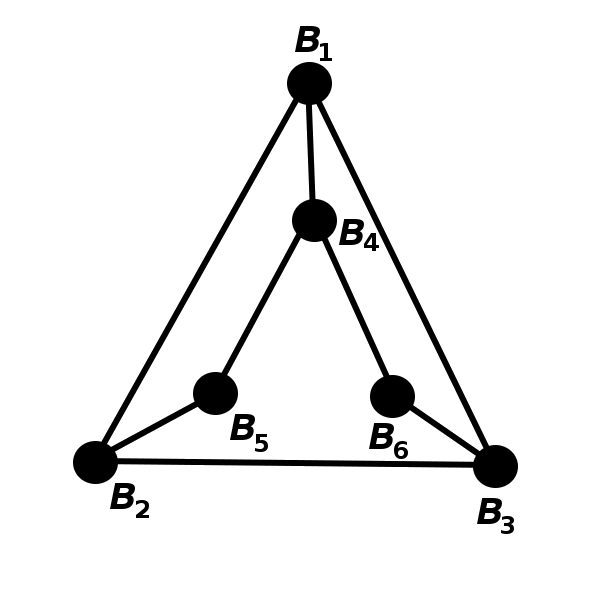 \(\quad\)
\(\quad\)
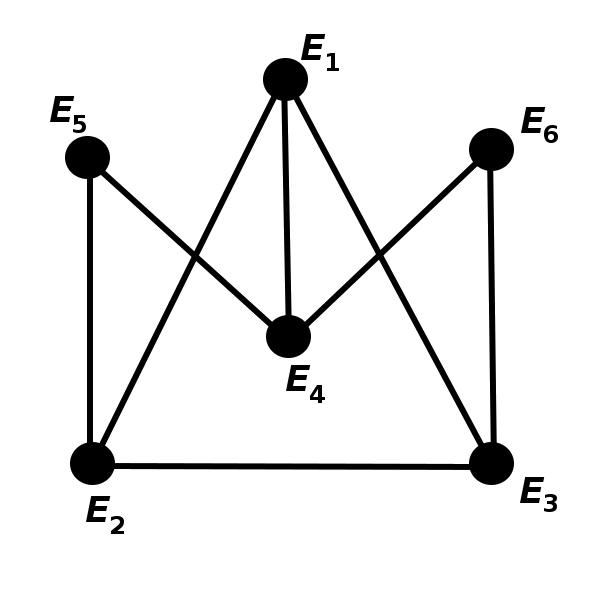 \(\quad\)
\(\quad\)