MTH 4140: Midterm 1 Practice 2

• (a) We must specify an ordered pair \(G=(V,E)\) such that \(V\) is a set and \(E\) a symmetric relation on \(V\). The set \(V\) has to contain \(5\) elements and the set \(E\) must contains \(14\) ordered pairs of elements in total.

  One such example is \(V=\left\{A,B,C,D,E\right\}\) and \(E=E_1\cup E_2\), where \(E_1=\left\{(A,B), (B,C), (C,D), (D,E), (E,A), (A,D), (A,C)\right\}\) and \(E_2=\left\{\left(u,v\right): (v,u)\in E_1\right\}\).

• (b) Let us denote the complement as \(\hat G=\left(G,\hat E\right)\). The set of vertices is the same \(V=\left\{A,B,C,D,E\right\}\) and the set of edges \(\hat E\) consists of exactly those ordered pairs \((u,v)\in V\times V\) that do not belong to \(E\). Therefore \[\hat E=\left\{ (B,D), (B,E),(C,E),(D,B),(E,B),(E,C) \right\}.\]

Recall that a non-trivial graph is an Eulerian trail if and only if the number of vertices of odd degree is at most \( 2 \). Therefore the answers are the following:

For the first graph the answer is no. The graph has two vertices of degree 5 and two vertices of degree 3;

For the second graph the answer is yes;

For the third graph the answer is no. The graph has three vertices of degree five and one vertex of degree 3.

Let us denote the graphs from left to right by \( G_1=\left(V_1,E_1\right) \), \( G_2=\left(V_2,E_2\right) \), and \( G_3=\left(V_3,E_3\right) \). Let us define the sets of vertices by \begin{eqnarray*} V_1&=&\left\{B_1,B_2, B_3,B_4,B_5,B_6\right\},\newline V_2&=&\left\{E_1,E_2, E_3,E_4,E_5,E_6\right\},\newline V_3&=&\left\{R_1,R_2, R_3,R_4,R_5,R_6\right\} \end{eqnarray*} and define the sets of edges in such a way that the graph representations are given in the pictures below

\(\quad\) \(\quad\)

Observe that the graph \( G_{3} \) is bipartite since the vertices of even degree can be colored in green and the vertices of odd degree can be colored in red and no two vertices of the same color are connected with an edge. On the other hand, the other two graphs contain cycles of length three. These cycles are \( \left(B_1,B_2,B_3\right) \) and \( \left(E_1,E_2,E_3\right) \). Therefore the graph \( G_{3} \) is isomorphic to neither of \( G_{1} \) and \( G_{2} \). On the other hand the graphs \( G_{1} \) and \( G_{2} \) are isomorphic. It is easy to verify that the function \( f:V_{1}\to V_{2} \) defined by \( f\left(B_i\right)=E_i \) for \( i\in\{1,2,\dots, 6\} \) is a bijection and the vertices \( B_i \) and \( B_j \) are adjacent in \( G_{1} \) if and only if the vertices \( E_i \) and \( E_j \) are adjacent in \( G_2 \) for every \( i, j\in\{1,2,\dots, 6\} \).

Each relation must be a subset of \( G\times G \). Let us define the relations \( \mu \) and \( \sigma \) in the following way: \begin{eqnarray*} \mu&=&\left\{({a},{b}),({b},{c}),({a},{c})\right\},\newline \sigma&=&\left\{({a},{b}),({b},{c})\right\}. \end{eqnarray*} The relation \( \mu \) is transitive. The relation \( \sigma \) is not transitive.

Let us define the following mathematical statement: \[ P(n)\equiv \left\{R_n=9^n-3\right\}.\]

The statement \( P(1) \) is true because \( 9^1-3=9-3=6=R_1 \).

Assume that \( k\geq 1 \) and that the statement \( P(k) \) is true. We need to prove that \( P(k+1) \) is true. In order to do so, we need to prove that \( R_{k+1}=9^{k+1}-3 \). Using the recursive relation \( R_{k+1}=9R_k+24 \) and the induction hypothesis \( R_k=9^k-3 \) we obtain \begin{eqnarray*} R_{k+1}&=&9R_k+24=9\cdot\left(9^k-3\right)+24\newline &=&9^{k+1}-9\cdot 3+24=9^{k+1}-3. \end{eqnarray*} This completes the proof that \( P(k+1)\equiv T \). Thus, by the principle of mathematical induction we are allowed to conclude that \( P(n)\equiv T \) for every \( n\geq 1 \).

The handshake theorem implies that the number of edges \( e \) of the graph satisfies \[ d(V_1)+d(V_2)+\cdots+d(V_{42})=2e.\] Thus the sum of the degrees is an even number. However, \[ d(V_1)+d(V_2)+\cdots+d(V_{42})=21+12+6+5+8+37\cdot 1=89\] is an odd number. We conclude that the desired graph does not exist.

First solution: We will prove this using an induction on \(k\). Let \(P(k)\) be the following statement: \[P(k)\equiv ^{\prime\prime} \mbox{There exists a graph that is triangle-free and has }C_5\mbox{ as a subgraph.}^{\prime\prime}\] The statement \(P(2)\) is true since the graph \(C_5\) satisfies the conditions.

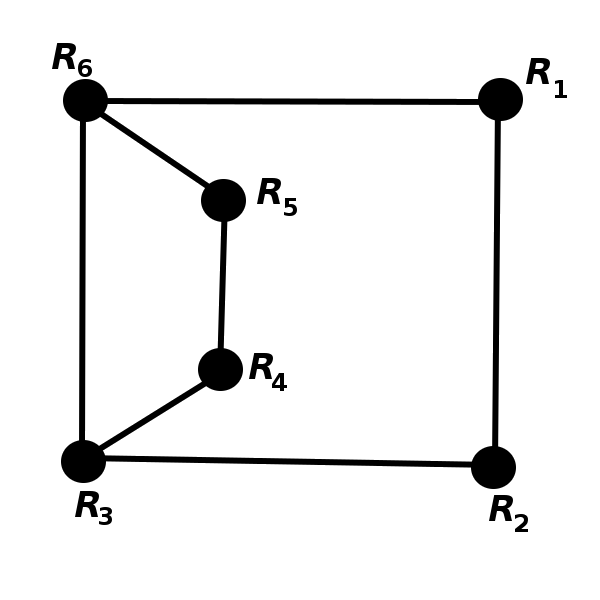
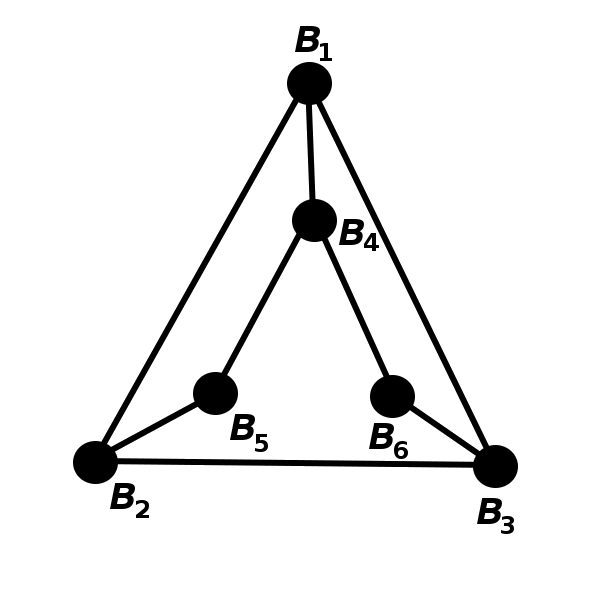
Assume that \(k\geq 3\) and that the statement \(P(k-1)\) is true. Consider the graph \(G_{k-1}=(V,E)\) such that each vertex has degree \(k-1\), there are no subgraphs \(C_3\) and there is a subgraph \(C_5\). Let us denote by \(A_1\), \(A_2\), \(\dots\), \(A_m\) the vertices of the graph \(G\).

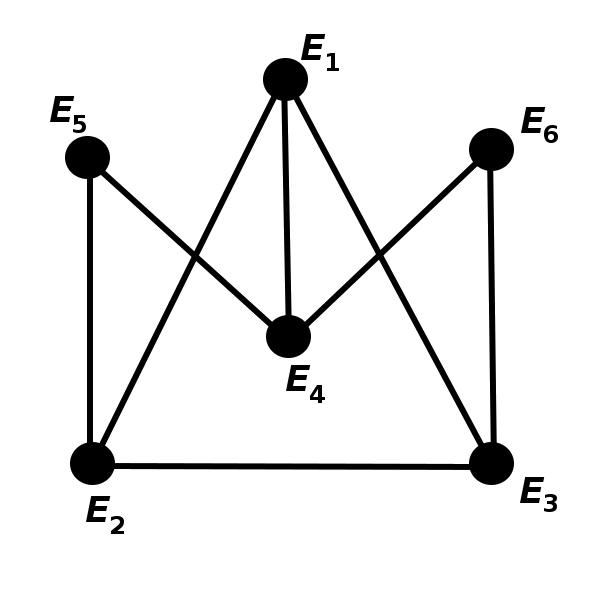
Consider a graph \(G^{\prime}_{k-1}=\left(V^{\prime},E^{\prime}\right)\) whose vertices are \(A_1^{\prime}\), \(A_2^{\prime}\), \(\dots\), \(A_m^{\prime}\) such that \(\left(A_i^{\prime},A_j^{\prime}\right)\in E^{\prime}\) if and only if \(\left(A_i,A_j\right)\in E\). In other words, the graph \(G^{\prime}_{k-1}\) is isomorphic to \(G_{k-1}\) with an isomorphism \(\varphi\) that maps \(A_i\) to \(A_i^{\prime}\) for each \(i\in\{1,2,\dots, m\}\).

Let us construct the graph \(G_{k+1}=\left(V_{k+1},E_{k+1}\right)\) with \(V_{k+1}=V\cup V^{\prime}\) and \(E_{k+1}\) is the union of all edges from \(E\) and \(E^{\prime}\), together with edges between \(A_i\) and \(A_i^{\prime}\) for every \(i\in\{1,2,\dots, m\}\).

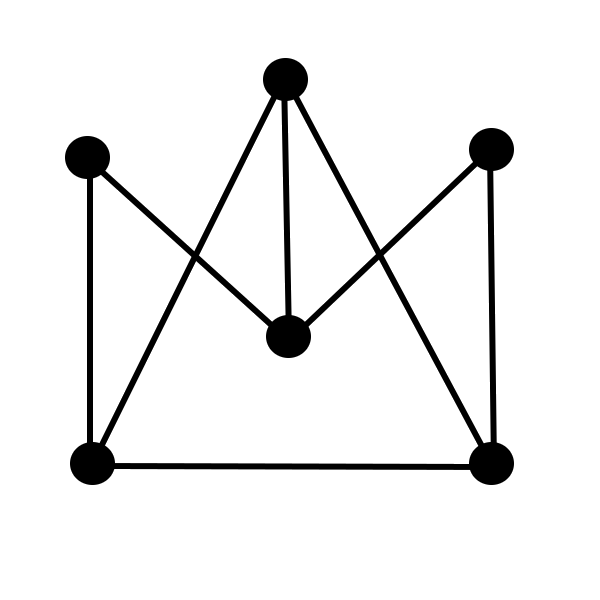
The graph \(G_{k+1}\) does not contain cycles of length \( 3\) because such cycles would have to be fully inside of one of the subgraphs isomorphic to \(G_{k-1}\). It does contain cycles of length \(5\) because it contains \(G_{k-1}\) as a subgraph.

Second solution: For \(k=2\), an example is \(C_5\). Assume that \(k\geq 3\). Let us consider the graph \(G_1=\left(V,E\right)\) whose set of vertices \(V\) consists of \(2^k\) sequences \(\left(a_1, a_2, \dots, a_k\right)\) of length \(k\) whose terms are from the set \(\{0,1\}\). Two vertices with labels \(\left(a_1, a_2, \dots, a_k\right)\) and \(\left(b_1, b_2, \dots, b_k\right)\) are connected with an edge if and only if the sequences differ in exactly one component. Since each vertex is labeled by a sequence with \(k\) terms, there are exactly \(k\) other sequences each of which differs in exactly one coordinate. Thus the degree of each vertex is \(k\).

We will now construct a graph \(G=\left(V,F\right)\) by using the same set of vertices \(V\) but by modifying the set of edges \(E\) and creating a new set \(F\). Let us denote by \(e_1\) the edge between \((0,0,0,\dots, 0)\) and \((1,0,0,\dots, 0)\) and by \(e_2\) the edge between \((0,1,0,\dots, 0)\) and \((1,1,0,\dots, 0)\). Let us denote by \(\overrightarrow z\) the sequence of \(k-3\) zeroes. With this helpful notation we can write \(e_1\) as the edge between \(\left(0,0,0,\overrightarrow z\right)\) and \(\left(1,0,0,\overrightarrow z\right)\). Similarly, \(e_2\) is the edge between \(\left(0,1,0,\overrightarrow z\right)\) and \(\left(1,1,0,\overrightarrow z\right)\). We will remove the edges \(e_1\) and \(e_2\) from the set \(E\), and add the following two edges: \begin{eqnarray*} f_1 &=& \mbox{edge between }\left(0,0,0,\overrightarrow z\right)\mbox{ and }\left((1,1,0,\overrightarrow z\right)\newline f_2 &=& \mbox{edge between }\left((1,0,0,\overrightarrow z\right)\mbox{ and }\left((0,1,0,\overrightarrow z\right). 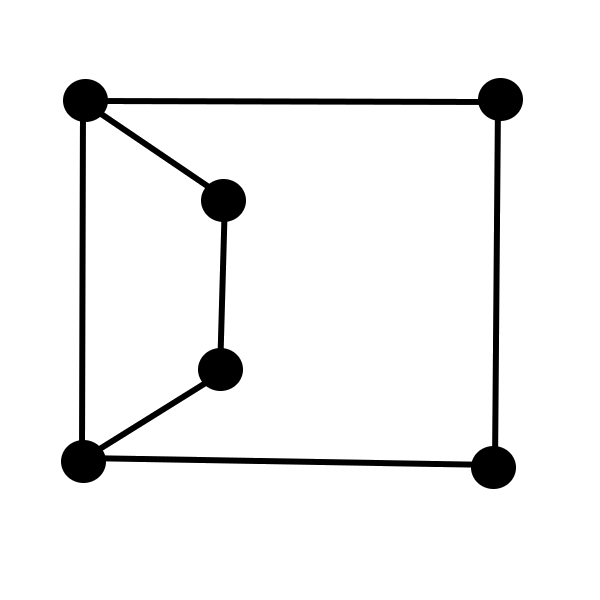\end{eqnarray*} Thus the set \(F\) is created in the following way: \[F=\left(E\setminus\left\{e_1,e_2\right\}\right)\cup \left\{f_1,f_2\right\}.\] Each vertex of the graph \((V,F)\) has degree \(k\). However, the graph \((V,F)\) is not bipartite because we will show that it has the following cycle of length \(5\): \begin{eqnarray*} \left(0,0,0,\overrightarrow z\right), \left(1,1,0,\overrightarrow z\right), \left(1,1,1,\overrightarrow z\right), \left(1,0,1,\overrightarrow z\right), \left(0,0,1,\overrightarrow z\right). \end{eqnarray*}