MTH 4140: Midterm 1 Practice 1
Assume that \(A\), \(B\), and \(C\) are three sets and that \(f:A\to B\) and \(g:B\to C\) are two functions. Consider the function \(h:A\to C\) defined as \(h(x)=g(f(x))\) for all \(x\in A\). Prove that if \(h\) is onto then \(g\) is onto as well.
Determine the number of bijections \(f:\{1,2,3,4,5\}\to\{4,5,6,7,8\}\) such that \(f(1)\) is even.
Let \(A=\{1,2,3,\dots, n\}\). Determine the number of binary relations on the set \(A\) that are reflexive but not symmetric.
Assume that the sequence \( a_n \) is defined as \( a_0=2 \), \( a_1=10 \), and \( a_{n+2}=10a_{n+1}-21a_n \) for every \( n\geq 0 \). Use the principle of mathematical induction to prove that \( a_n=3^n+7^n \) for all \( n\geq 0 \).
Let \(V=\{1,2,3,4,5\}\) be the vertices of a graph \(G\). Two vertices \(i\) and \(j\) are joined by an edge if and only if \(i+j\) is odd. Draw the graph \(G\).
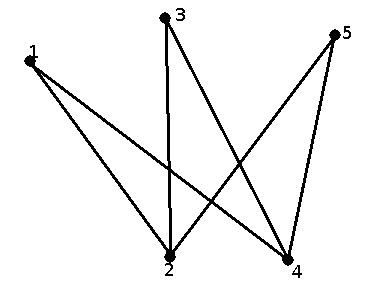
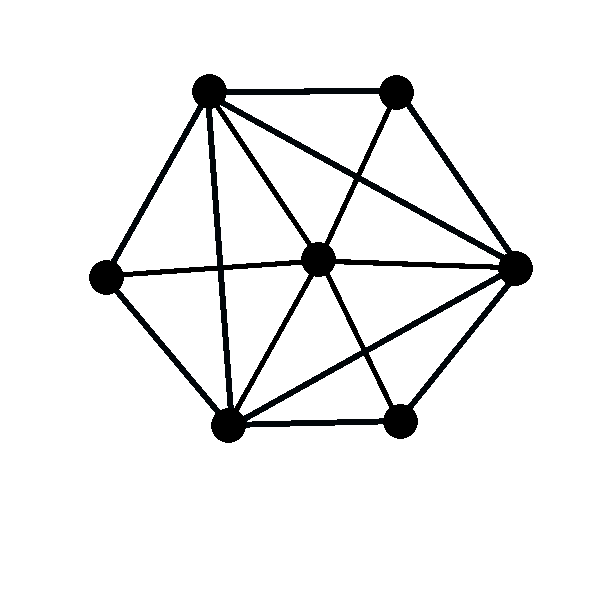
Determine the complement of the graph shown in the picture below.
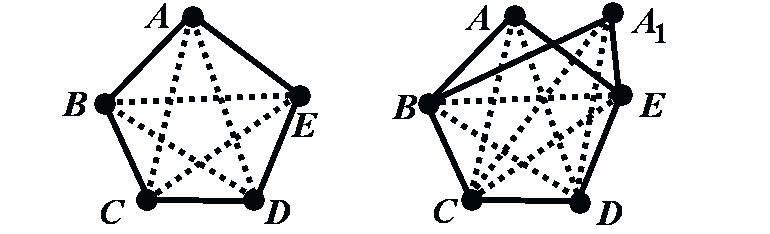
Determine which of the pairs of graphs below are isomorphic.
Assume that the graph \(G\) can be drawn without lifting pen from the paper and without tracing the same line twice and that this drawing can be made in such a way that it starts and ends in the same vertex. Prove that the graph \(G\) does not have cut edges.
Prove that for each integer \(k\geq 2\) there exists a bipartite graph \(G\) with \(2^k\) vertices whose each vertex has degree \(k\).
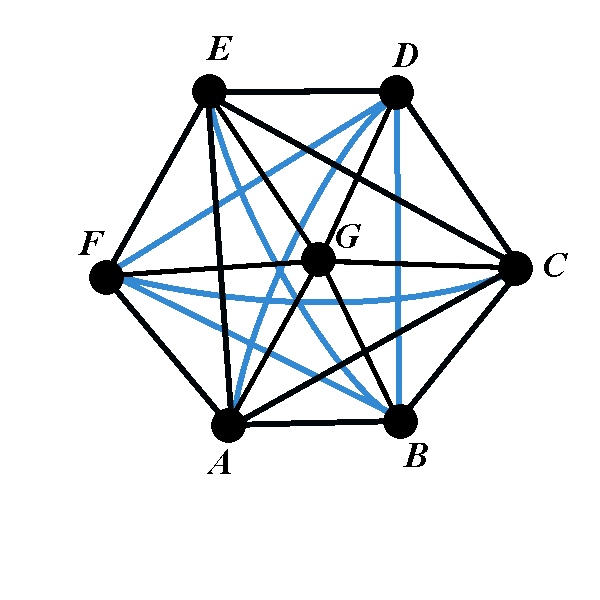
A graph is called red-green triangle free if all of its edges can be painted in red and green in such a way that there is neither a red triangle nor a green triangle. What is the maximal number \(e\) of edges that a red-green triangle free graph can have, if the graph has \(6\) vertices?