MTH4140: Final Practice 1
Provide an example of a function that is injective but not surjective and that has the codomain \( H=\left\{k,l,m,3,4\right\} \).
The sequence \( (a_n)_{n=1}^{\infty} \) satisfies \( a_1=4 \) and \[ a_{n+1}=9a_n+40,\quad\mbox{for }n\geq 1.\] Use the principle of mathematical induction to prove that \( a_n=9^n-5 \) for every integer \( n\geq1 \).
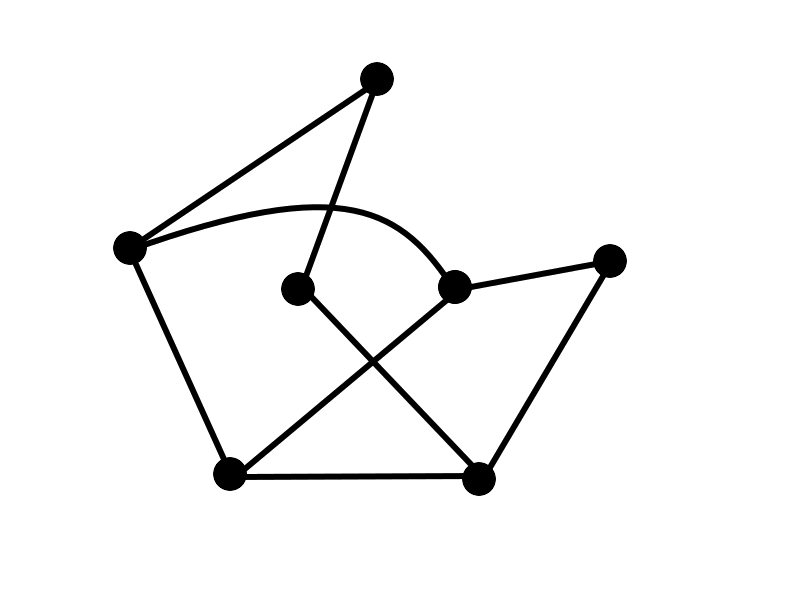
Determine an ordered pair of a set and a relation that correspond to the following graph:
Let \[ V=\left\{5,9,10,51,52,53,55,56,101,105\right\}.\] Let \( E\subseteq V\times V \) be the relation defined as \( (a,b)\in E \) if and only if \( 0< |a-b|\leq 30 \). Determine the chromatic polynomial of the graph \( G=(V,E) \).
Assume that \( G \) is a graph that can be placed in a plane in such a way that no two edges intersect except at vertices. The graph has exactly \( 158 \) vertices. Exactly \( 31 \) of the vertices have degree \( 5 \), exactly \( 90 \) of the vertices have degree \( 4 \), and exactly \( 37 \) of the vertices have degree \( 3 \). Determine the total number of regions in which the plane is partitioned when the graph \( G \) is drawn.
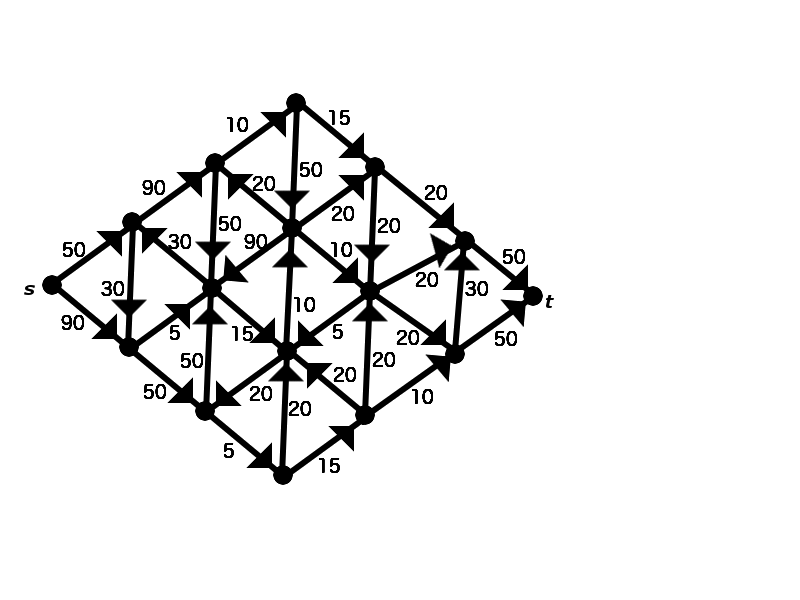
Determine the value of the maximal flow from \( s \) to \( t \) in the directed graph shown below.
It is known that the chromatic number of the graph \( G=(V,E) \) is equal to \( 4 \) and that there exists a proper coloring of the vertices in which there are seventeen vertices of color 1, five vertices of color 2, twenty vertices of color 3, and fifty vertices of color 4. Prove that the graph is not Hamiltonian.