MTH 3030: Final Practice 1
Determine whether the series \( \displaystyle \sum_{n=1}^{\infty}\frac{n^{6}-7n^{5}+8}{4n^{7}+7n^{6}+4} \) is convergent or divergent.
Find a symmetric equation of the plane that contains the points \( A(5,3,6) \), \( B(0,3,9) \), and \( C(4,-6,5) \).
Assume that \( A(t)=t^3-2t \), \( B(t)=2t+5 \), and \( C(t)=t^2+5t \), and assume that \( f(x,y,z) \) is a differentiable function such that \( \nabla f(-1,7,6)=\langle 3,6,4\rangle \). Assume that the function \( g \) is defined as \( g(t)=f(A(t),B(t),C(t)) \). Determine \( g^{\prime}(1) \).
Determine whether the series \( \displaystyle \sum_{n=1}^{\infty}\frac{7-3\sin^3 n}{n+6} \) is convergent or divergent.
Evaluate the integral \( \displaystyle\int_{1}^{3}\int_{2}^{5} \int_{3}^{5}\left(3z-y\right)\,dydzdx \).
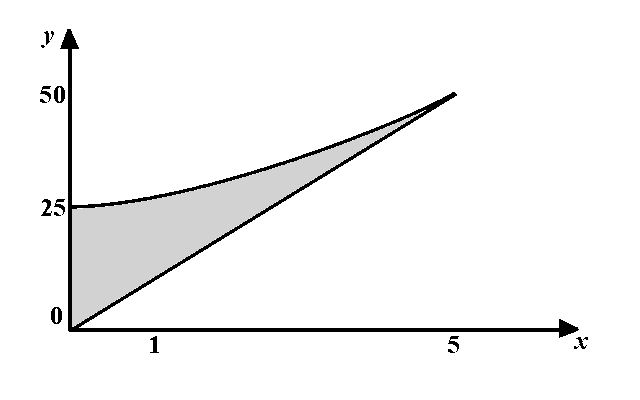
Consider the region \( D \) in the \( xy \) plane defined as \( D=\left\{(x,y): 10\leq 10x \leq y\leq x^2+25\right\} \).
- (a) Sketch the region \( D \).
- (b) Evaluate the integral \( \displaystyle \iint_Dx\,dA \).
Determine and classify the critical points of the function \( f(x,y)=195y+18xy+y^3-3x^2+30 \).
Evaluate the integral \( \displaystyle\iint_R \frac1{x^2y}\,dA \) where \( R \) is the set of points \( (x,y) \) that satisfy the following two conditions: \begin{eqnarray*} 3x+7\leq &y&\leq 3x+9\newline 4x\leq &y&\leq 8x. \end{eqnarray*}
The minimum of the differentiable function \( F(x,y) \) on the curve \( x^2=6y^2-15 \) is attained at the point \( (3,2) \). It is given that \( F_x(3,2)=24 \). Determine \( F_y(3,2) \).
For each of the following statements determine whether it is true or false. If the statement is true, provide a mathematically rigorous proof of the statement. If the statement is false, provide a counter-example.
- (a) If \( (a_n) \) is a sequence of positive real numbers such that \( \displaystyle\frac{a_n}2\leq a_{n+1}\leq \frac{a_n+\frac{a_n}n}2 \) then the series \( \displaystyle \sum_{n=1}^{\infty}a_n \) is convergent.
- (b) If \( f \) is a positive function such that \( \displaystyle \lim_{x\to+\infty} f(x)=0 \) and the integral \( \displaystyle \int_1^{+\infty}f(x)\,dx \) is convergent, then the series \( \displaystyle \sum_{n=1}^{\infty}(-1)^nf(n) \) is convergent.
- (c) Assume that \( (a_n) \) and \( (b_n) \) are sequences of real numbers such that \( \displaystyle \sum_{n=1}^{\infty} a_n \) and \( \displaystyle \sum_{n=1}^{\infty} b_n \) are convergent. Then the series \( \displaystyle \sum_{n=1}^{\infty} a_nb_n \) is convergent as well.
- (d) Assume that \( (a_n) \) and \( (b_n) \) are sequences of real numbers such that \( a_n\geq 0 \) and \( b_n\geq 0 \) for all \( n \). If \( \displaystyle \sum_{n=1}^{\infty}(-1)^na_n \) and \( \displaystyle \sum_{n=1}^{\infty}(-1)^nb_n \) are convergent, then \( \displaystyle \sum_{n=1}^{\infty}(-1)^na_nb_n \) is convergent as well.