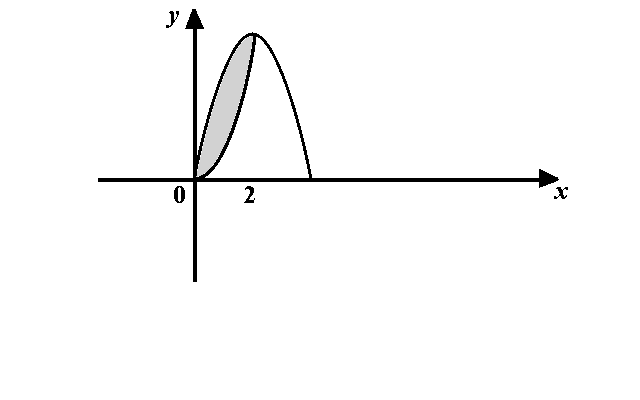MTH 2610: Final Practice 1
Evaluate the limit \( \displaystyle \lim_{x\to 1}\frac{x-1}{\sqrt{ 7x+9 }-4} \).
Find all numbers \( x \) that satisfy the equation \( \log_{2}\left(x^2-3x-54\right)=4 \).
Find the area bounded by \( y=48x-12x^2 \) and the \( x \) axis.
Use the linearization of the function that satisfies the criteria \( f(4)=12 \) and \( f^{\prime}(4)=6 \) to approximate \( f(3.8) \).
Assume that the function \( f \) is defined for \( x\geq 0 \) in the following way: \( \displaystyle f(x)=\frac{4x-2}{x+3} \). Determine the inverse function of \( f \).
If \( \displaystyle x^{6}e^y+5=xy^{3} \), determine \( \displaystyle\frac{dy}{dx} \).
Find the derivative of \( \displaystyle y=\ln\left(\frac{(x-8)^{\frac1{2}}(x+3)}{x}\right) \).
Find the derivative of the function \( \displaystyle f(x)=x^{\ln\left(x^{8}\right)} \).
The value of the expression \( x\cdot y \), with both variables positive, is \( 12 \). What is the smallest value of \( 3x+4y \)?
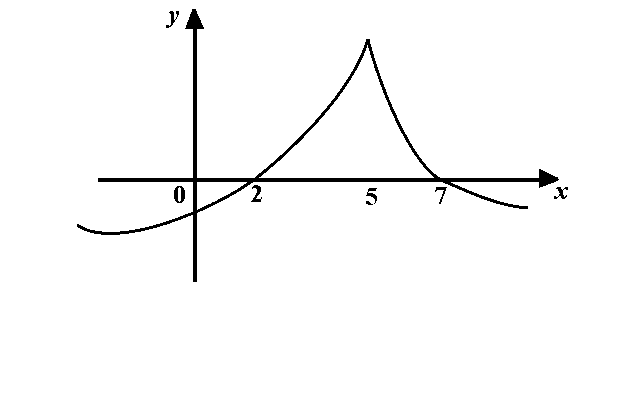
Sketch the graph of a function \( f \) that has the following characteristics: \begin{eqnarray*} &&f(2)=f(7)=0\newline && f^{\prime}(x)> 0 \;\mbox{for }x< 5\newline &&f^{\prime}(5) \;\mbox{does not exist}\newline && f^{\prime}(x)< 0 \;\mbox{for }x> 5\newline && f^{\prime\prime}(x)> 0\;\mbox{for }x\neq 5. \end{eqnarray*}
The triangle \( ABC \) has right angle at vertex \( A \). The sides of the triangle satisfy \( AB=12 \) and \( AC=6 \). What is the maximal possible area of a rectangle that can be inscribed in the triangle \( ABC \) if one of its vertices is \( A \) and another vertex \( P \) must belong to the edge \( BC \)?
Evaluate the integral \( \displaystyle\int_{4}^{6}\frac{2\sqrt{x-1} +4}{x\sqrt{x-1} }\,dx \).
Consider the functions \( f(x)=x^3 \) and \( g(x)=16x-6x^2 \).
- (a) Sketch the region \( R \) in the \( xy \) plane that is located between the graphs of the functions \( f \) and \( g \) for \( x\geq 0 \).
- (b) Evaluate the area of the region \( R \) from the previous part of the problem.
Do there exist two functions \( f:\mathbb R\to\mathbb R \) and \( g:\mathbb R\to\mathbb R \) that are both onto but the function \( h:\mathbb R\to\mathbb R \) defined as \( h(x)=f(x)+12g(x) \) is not onto? Explain your answer.
The symbol \( \mathbb R \) denotes the set of all real numbers.
Prove that for every differentiable function \( f \) such that \( \displaystyle\int_0^{ 7 }f(t)\,dt=\int_0^{7}e^{-t^4}\,dt \) there exists \( c \) that satisfies \( 0\leq c\leq 7 \) and \( e^{c^4}\cdot f(c)=1 \).