MTH2205 Home
MTH 2205: Final Practice 2 (Part 1: No calculators)
Problem 1. Find the absolute minimum value of \(f(x)=\frac{2x}{x^2+1}\) on the interval \(0\leq x\leq 2\).
(A) \(-1\) \(\quad\quad\) (B) \(0\) \(\quad\quad\) (C) \(1\) \(\quad\quad\) (D) \(\frac45\) \(\quad\quad\) (E) \(2\)
(A) \(-1\) \(\quad\quad\) (B) \(0\) \(\quad\quad\) (C) \(1\) \(\quad\quad\) (D) \(\frac45\) \(\quad\quad\) (E) \(2\)
Problem 2. The functions \(f(x)\) and \(f^{-1}(x)\) are inverses of one another, where \(f(-1)=5\), \(f'(5)=7\), and \(f'(-1)=4\). Then \(\left(f^{-1}\right)'(5)\) is
(A) \(-4\) \(\quad\quad\) (B) \(\frac15\) \(\quad\quad\) (C) \(\frac17\) \(\quad\quad\) (D) \(\frac14\) \(\quad\quad\) (E) \(-5\)
(A) \(-4\) \(\quad\quad\) (B) \(\frac15\) \(\quad\quad\) (C) \(\frac17\) \(\quad\quad\) (D) \(\frac14\) \(\quad\quad\) (E) \(-5\)
Problem 3. The cost of producing \(x\) items is \(C(x)=2x^3-20x^2+100x\). Find the value of \(x\) that minimizes the average cost.
(A) \(5\) \(\quad\quad\) (B) \(6\) \(\quad\quad\) (C) \(3\) \(\quad\quad\) (D) \(8\) \(\quad\quad\) (E) \(2\)
(A) \(5\) \(\quad\quad\) (B) \(6\) \(\quad\quad\) (C) \(3\) \(\quad\quad\) (D) \(8\) \(\quad\quad\) (E) \(2\)
Problem 4. Solve for \(x\): \(\left(\frac13\right)^{1-x}=9\).
(A) \(-2\) \(\quad\quad\) (B) \(0\) \(\quad\quad\) (C) \(-1\) \(\quad\quad\) (D) \(2\) \(\quad\quad\) (E) \(3\)
(A) \(-2\) \(\quad\quad\) (B) \(0\) \(\quad\quad\) (C) \(-1\) \(\quad\quad\) (D) \(2\) \(\quad\quad\) (E) \(3\)
Problem 5. Solve for \(x\): \(\log_2(x)+\log_2(x-7)=3\).
(A) \(x=1\) and \(x=8\) \(\quad\quad\) (B) \(x=-1\) only \(\quad\quad\) (C) \(x=8\) only \(\quad\quad\)
(D) \(x=3\) and \(x=4\) \(\quad\quad\) (E) \(x=-1\) and \(x=8\)
(A) \(x=1\) and \(x=8\) \(\quad\quad\) (B) \(x=-1\) only \(\quad\quad\) (C) \(x=8\) only \(\quad\quad\)
(D) \(x=3\) and \(x=4\) \(\quad\quad\) (E) \(x=-1\) and \(x=8\)
Problem 6. If \(f(x)=xe^{x^2+1}\), then \(f'(2)\) is
(A) \(9e^5\) \(\quad\quad\) (B) \(6e^5\) \(\quad\quad\) (C) \(2e^5\) \(\quad\quad\) (D) \(8e^5\) \(\quad\quad\) (E) \(e^4\)
(A) \(9e^5\) \(\quad\quad\) (B) \(6e^5\) \(\quad\quad\) (C) \(2e^5\) \(\quad\quad\) (D) \(8e^5\) \(\quad\quad\) (E) \(e^4\)
Problem 7. \(\int_0^4\frac1{3x+1}\,dx=\)
(A) \(\frac1{13}\) \(\quad\quad\) (B) \(\frac1{13}\ln4\) \(\quad\quad\) (C) \(\frac1{3}\ln13\) \(\quad\quad\) (D) \(\frac14\) \(\quad\quad\) (E) \(\frac3{3x+1}\)
(A) \(\frac1{13}\) \(\quad\quad\) (B) \(\frac1{13}\ln4\) \(\quad\quad\) (C) \(\frac1{3}\ln13\) \(\quad\quad\) (D) \(\frac14\) \(\quad\quad\) (E) \(\frac3{3x+1}\)
Problem 8. Find \(\frac{dy}{dx}\) for \(y=\ln\left(\frac{\sqrt{x-5}}{4x^3+1}\right)\).
(A) \(\frac{\sqrt{x-5}}{4x^3+1}\) \(\quad\quad\) (B) \(\frac1{2(x-5)}-\frac{12x^2}{4x^3+1}\) \(\quad\quad\) (C) \(\frac{4x^3+1}{\sqrt{x-5}}\) \(\quad\quad\)
(D) \(e^{\sqrt{x-5}}-e^{4x^3+1}\) \(\quad\quad\) (E) \(\frac1{2\sqrt{x-5}}-\frac{12x^2}{4x^3+1}\)
(A) \(\frac{\sqrt{x-5}}{4x^3+1}\) \(\quad\quad\) (B) \(\frac1{2(x-5)}-\frac{12x^2}{4x^3+1}\) \(\quad\quad\) (C) \(\frac{4x^3+1}{\sqrt{x-5}}\) \(\quad\quad\)
(D) \(e^{\sqrt{x-5}}-e^{4x^3+1}\) \(\quad\quad\) (E) \(\frac1{2\sqrt{x-5}}-\frac{12x^2}{4x^3+1}\)
Problem 9. If the second derivative of \(f(x)\) is \(f''(x)=(3-x)(x^2-4)\), on what interval(s) is \(f(x)\) concave up?
(A) \((-\infty,-2)\) and (2,3) \(\quad\quad\) (B) \((-2,2)\) \(\quad\quad\) (C) \((-\infty,\infty)\) \(\quad\quad\)
(D) \((2,\infty)\) \(\quad\quad\) (E) \((-2,2)\) and \((3,\infty)\)
(A) \((-\infty,-2)\) and (2,3) \(\quad\quad\) (B) \((-2,2)\) \(\quad\quad\) (C) \((-\infty,\infty)\) \(\quad\quad\)
(D) \((2,\infty)\) \(\quad\quad\) (E) \((-2,2)\) and \((3,\infty)\)
Problem 10. The graph of \(f'(x)\), the derivative of \(f\), is given below for \(-6\leq x\leq 7\). On what intervals is the function, \(f(x)\), increasing?
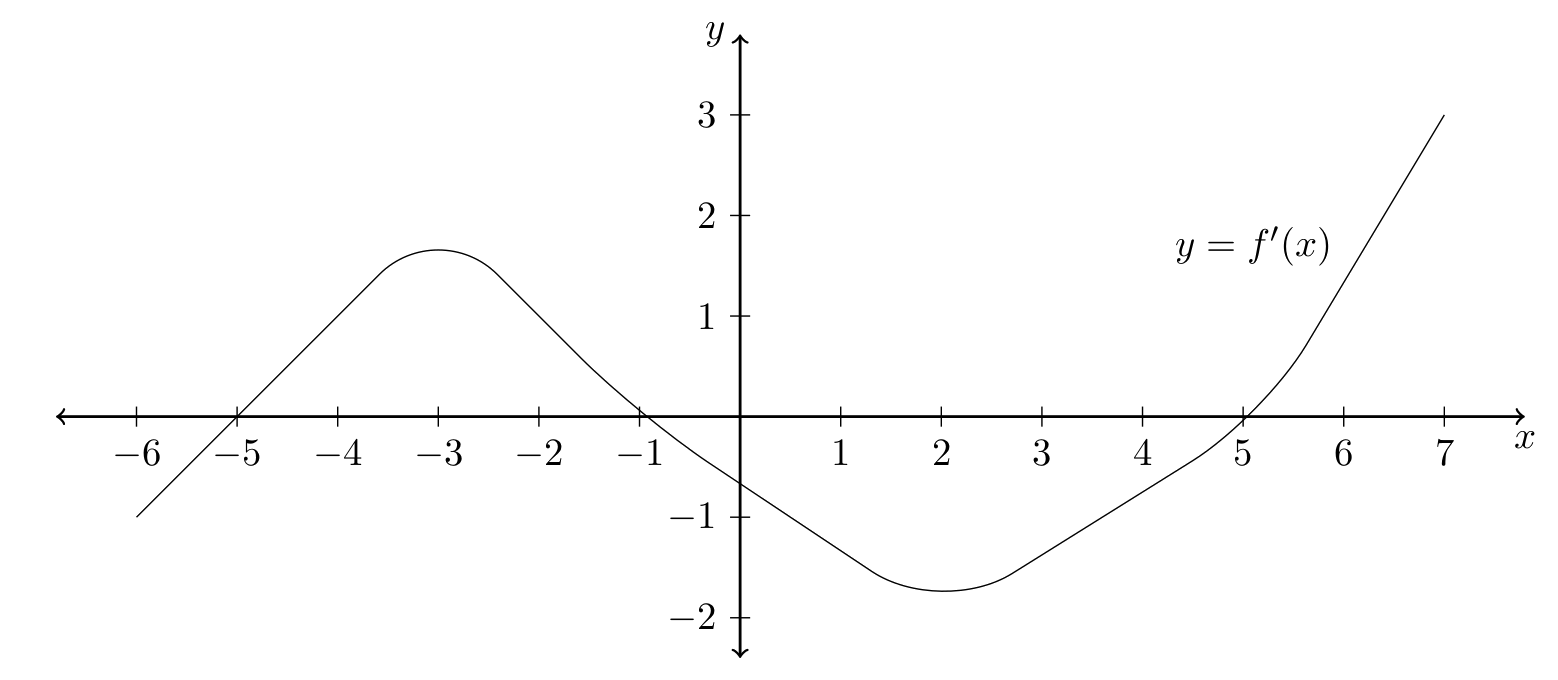
(A) \((-3,2)\) \(\quad\quad\) (B) \((-3,7)\) \(\quad\quad\) (C) \((-5,-1)\) and \((5,7)\) \(\quad\quad\)
(D) \((-6,-3)\) and \((2,7)\) \(\quad\quad\) (E) \((-6,-5)\) and \((-1,5)\)
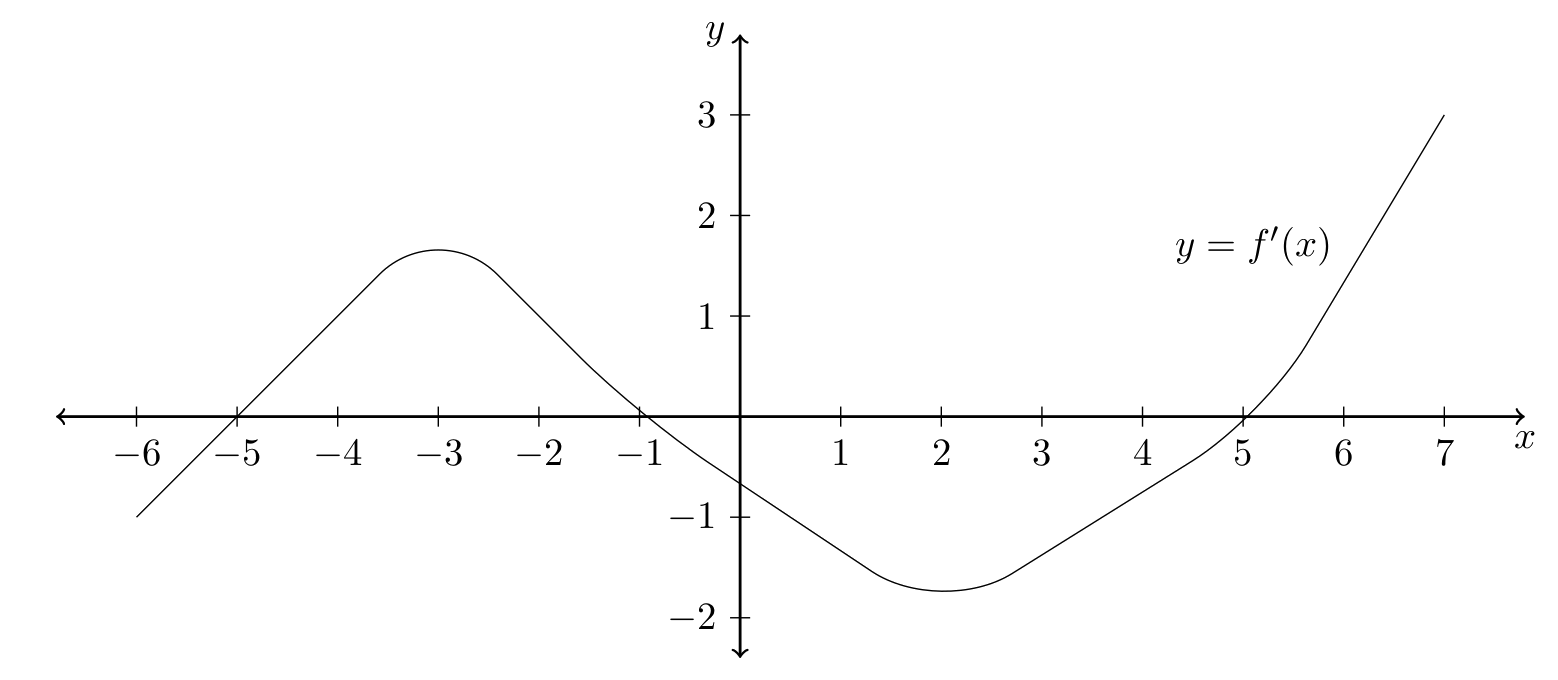
(A) \((-3,2)\) \(\quad\quad\) (B) \((-3,7)\) \(\quad\quad\) (C) \((-5,-1)\) and \((5,7)\) \(\quad\quad\)
(D) \((-6,-3)\) and \((2,7)\) \(\quad\quad\) (E) \((-6,-5)\) and \((-1,5)\)
Problem 11. The graph of \(y=f(x)\) is given below. Evaluate \(\int_0^4f(x)\,dx\).
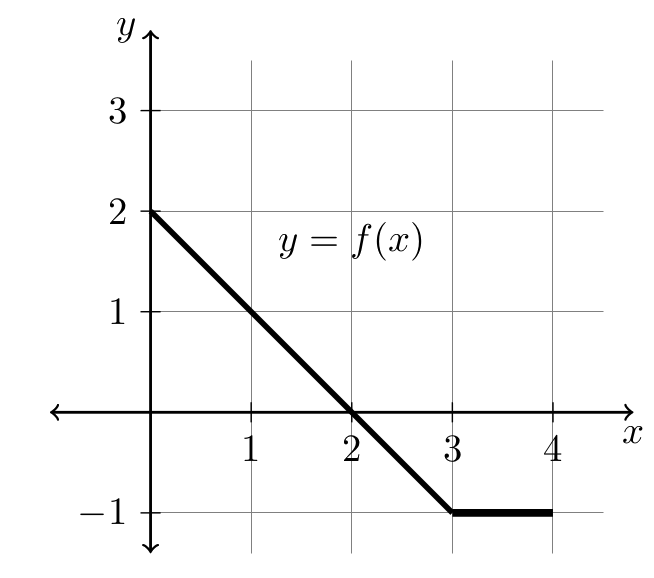
(A) \(0.5\) \(\quad\quad\) (B) \(1.5\) \(\quad\quad\) (C) \(-0.5\) \(\quad\quad\) (D) \(3.5\) \(\quad\quad\) (E) \(-2.5\)
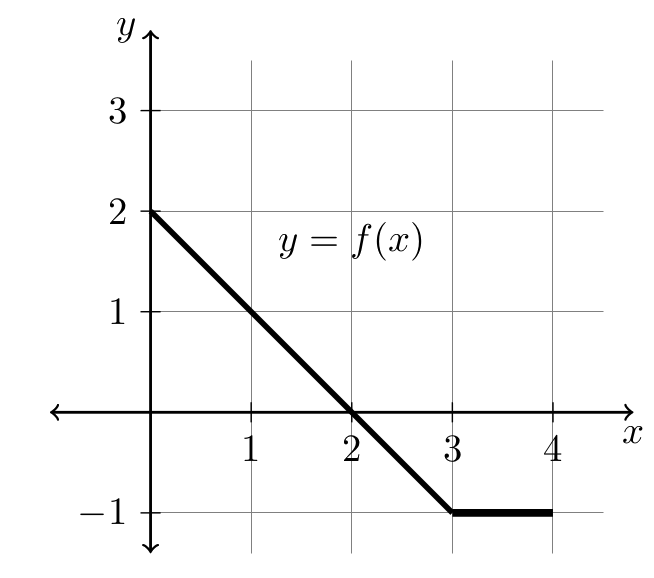
(A) \(0.5\) \(\quad\quad\) (B) \(1.5\) \(\quad\quad\) (C) \(-0.5\) \(\quad\quad\) (D) \(3.5\) \(\quad\quad\) (E) \(-2.5\)
Problem 12. An object moving on a line has velocity given by \(v(t)=3t^2-4t+6\), \(t\geq 0\). At time \(t=1\) the object's position is \(s(1)=2\). Find \(s(t)\), the object's position at any time \(t\).
(A) \(s(t)=t^3-2t^2+6t+2\) \(\quad\quad\) (B) \(s(t)=6t-4\) \(\quad\quad\) (C) \(s(t)=t^3-2t^2+6t-3\) \(\quad\quad\)
(D) \(s(t)=t^4-2t^3+6t^2-3\) \(\quad\quad\) (E) \(s(t)=5\)
(A) \(s(t)=t^3-2t^2+6t+2\) \(\quad\quad\) (B) \(s(t)=6t-4\) \(\quad\quad\) (C) \(s(t)=t^3-2t^2+6t-3\) \(\quad\quad\)
(D) \(s(t)=t^4-2t^3+6t^2-3\) \(\quad\quad\) (E) \(s(t)=5\)
Problem 13. Linearize \(f(x)=x^4\) at \(x=2\), and then use the linearization to approximate \(f(2.01)\).
(A) \(16.01\) \(\quad\quad\) (B) \(16.24\) \(\quad\quad\) (C) \(18.24\) \(\quad\quad\) (D) \(16.32\) \(\quad\quad\) (E) \(16.04\)
(A) \(16.01\) \(\quad\quad\) (B) \(16.24\) \(\quad\quad\) (C) \(18.24\) \(\quad\quad\) (D) \(16.32\) \(\quad\quad\) (E) \(16.04\)
Problem 14. If \(f(x)=\frac{4x-1}{2x+3}\), then the inverse function \(f^{-1}(x)\) is
(A) \(\frac{2x+3}{4x-1}\) \(\quad\quad\) (B) \(\frac{1-4x}{3-2x}\) \(\quad\quad\) (C) \(\frac{4-2x}{3x+1}\) \(\quad\quad\)
(D) \(\frac{3x+1}{4-2x}\) \(\quad\quad\) (E) \(3x+1+\frac1{4-2x}\)
(A) \(\frac{2x+3}{4x-1}\) \(\quad\quad\) (B) \(\frac{1-4x}{3-2x}\) \(\quad\quad\) (C) \(\frac{4-2x}{3x+1}\) \(\quad\quad\)
(D) \(\frac{3x+1}{4-2x}\) \(\quad\quad\) (E) \(3x+1+\frac1{4-2x}\)
Problem 15. The function \(f(x)=4x^3+9x^2+6x-5\) has a point of inflection at
(A) \(x=1\) \(\quad\quad\) (B) \(x=-\frac12\) \(\quad\quad\) (C) \(x=\frac14\) \(\quad\quad\)
(D) \(x=-\frac34\) \(\quad\quad\) (E) \(x=-\frac12\) and \(x=-1\)
(A) \(x=1\) \(\quad\quad\) (B) \(x=-\frac12\) \(\quad\quad\) (C) \(x=\frac14\) \(\quad\quad\)
(D) \(x=-\frac34\) \(\quad\quad\) (E) \(x=-\frac12\) and \(x=-1\)
Problem 16. Evaluate \(\displaystyle \int_1^4\left(3\sqrt x+\frac{4}{x^2}\right)\,dx\)
(A) \(6\) \(\quad\quad\) (B) \(7\) \(\quad\quad\) (C) \(18\) \(\quad\quad\) (D) \(10\) \(\quad\quad\) (E) \(17\)
(A) \(6\) \(\quad\quad\) (B) \(7\) \(\quad\quad\) (C) \(18\) \(\quad\quad\) (D) \(10\) \(\quad\quad\) (E) \(17\)
Problem 17. Evaluate \(\displaystyle \sum_{i=1}^4i(4-i)\)
(A) \(0\) \(\quad\quad\) (B) \(-10\) \(\quad\quad\) (C) \(10\) \(\quad\quad\) (D) \(9\) \(\quad\quad\) (E) \(-9\)
(A) \(0\) \(\quad\quad\) (B) \(-10\) \(\quad\quad\) (C) \(10\) \(\quad\quad\) (D) \(9\) \(\quad\quad\) (E) \(-9\)
Problem 18. \(\displaystyle \int \left(x^3+2x\right)^5\left(12x^2+8\right)\,dx\)
(A) \(\frac16\left(x^3+2x\right)^6+C\) \(\quad\quad\) (B) \(\frac16\left(x^3+2x\right)^6\cdot\frac12\left(12x^2+8\right)^2+C\) \(\quad\quad\) (C) \(\frac12\left(12x^2+8\right)^2+C\) \(\quad\quad\)
(D) \(\frac23\left(x^3+2x\right)^6+C\) \(\quad\quad\) (E) \(\left(x^3+2x\right)^6+C\)
(A) \(\frac16\left(x^3+2x\right)^6+C\) \(\quad\quad\) (B) \(\frac16\left(x^3+2x\right)^6\cdot\frac12\left(12x^2+8\right)^2+C\) \(\quad\quad\) (C) \(\frac12\left(12x^2+8\right)^2+C\) \(\quad\quad\)
(D) \(\frac23\left(x^3+2x\right)^6+C\) \(\quad\quad\) (E) \(\left(x^3+2x\right)^6+C\)
Problem 19. Solve the differential equation
\(\frac{dy}{dx}=\frac{x^2}{y^2}\), \(y\neq 0\), with the initial condition \(y(0)=2\).
(A) \(y=\sqrt{x^2+8}\) \(\quad\quad\) (B) \(y=x+8\) \(\quad\quad\) (C) \(y=\sqrt{x^3+1}\) \(\quad\quad\)
(D) \(y=\sqrt[3]{x^3+1}\) \(\quad\quad\) (E) \(y=\sqrt[3]{x^3+8}\)
(A) \(y=\sqrt{x^2+8}\) \(\quad\quad\) (B) \(y=x+8\) \(\quad\quad\) (C) \(y=\sqrt{x^3+1}\) \(\quad\quad\)
(D) \(y=\sqrt[3]{x^3+1}\) \(\quad\quad\) (E) \(y=\sqrt[3]{x^3+8}\)
Problem 20. The demand equation is \(x+3p^2=1000\), where \(p\) is the price. Find the elasticity of demand if \(p=10\).
(A) \(-\frac49\) \(\quad\quad\) (B) \(-\frac16\) \(\quad\quad\) (C) \(-2\) \(\quad\quad\) (D) \(-\frac67\) \(\quad\quad\) (E) \(-\frac58\)
(A) \(-\frac49\) \(\quad\quad\) (B) \(-\frac16\) \(\quad\quad\) (C) \(-2\) \(\quad\quad\) (D) \(-\frac67\) \(\quad\quad\) (E) \(-\frac58\)
Problem 21. The difference of one number \(x\) and twice a second number \(y\) is \(16\). What is the minimum possible product of \(x\) and \(y\)?
(A) \(-32\) \(\quad\quad\) (B) \(-24\) \(\quad\quad\) (C) \(80\) \(\quad\quad\) (D) \(12\) \(\quad\quad\) (E) \(-48\)
(A) \(-32\) \(\quad\quad\) (B) \(-24\) \(\quad\quad\) (C) \(80\) \(\quad\quad\) (D) \(12\) \(\quad\quad\) (E) \(-48\)
Problem 22. The function \(f(x)=2x^3+3x^2-36x\) has a relative maximum at
(A) \(x=-3\) \(\quad\quad\) (B) \(x=-2\) \(\quad\quad\) (C) \(x=0\) \(\quad\quad\) (D) \(x=2\) \(\quad\quad\) (E) \(x=3\)
(A) \(x=-3\) \(\quad\quad\) (B) \(x=-2\) \(\quad\quad\) (C) \(x=0\) \(\quad\quad\) (D) \(x=2\) \(\quad\quad\) (E) \(x=3\)
Problem 23. The approximate area bounded by \(y=5-x^2\), the \(x\)-axis, \(x=-1\) and \(x=2\), using three rectangles of equal width and right hand endpoints is:
(A) \(9\) \(\quad\quad\) (B) \(10\) \(\quad\quad\) (C) \(11\) \(\quad\quad\) (D) \(12\) \(\quad\quad\) (E) \(13\)
(A) \(9\) \(\quad\quad\) (B) \(10\) \(\quad\quad\) (C) \(11\) \(\quad\quad\) (D) \(12\) \(\quad\quad\) (E) \(13\)
Problem 24. If \(f(2)=7\), \(f'(2)=0\), and \(f''(2)=-5\), then the point \((2,7)\) is
(A) a relative maximum \(\quad\quad\) (B) a relative minimum \(\quad\quad\) (C) a point of inflection \(\quad\quad\)
(D) a point of discontinuity \(\quad\quad\) (E) none of the above
(A) a relative maximum \(\quad\quad\) (B) a relative minimum \(\quad\quad\) (C) a point of inflection \(\quad\quad\)
(D) a point of discontinuity \(\quad\quad\) (E) none of the above
Problem 25. Find the average value of \(f(x)=4x-x^2\) on the interval \(0\leq x\leq 2\).
(A) \(\frac{16}3\) \(\quad\quad\) (B) \(2\) \(\quad\quad\) (C) \(4\) \(\quad\quad\) (D) \(8\) \(\quad\quad\) (E) \(\frac83\)
(A) \(\frac{16}3\) \(\quad\quad\) (B) \(2\) \(\quad\quad\) (C) \(4\) \(\quad\quad\) (D) \(8\) \(\quad\quad\) (E) \(\frac83\)