IMO Problem Collection: Table of contents
The 55th International Mathematical Olympiad: Problems and Solutions
Day 1 (July 8, 2014)
Let \(a_0 < a_1 < a_2 < \cdots\) be an infinite sequence of positive integers. Prove that there exists a unique integer \(n\geq 1\) such that \[a_n < \frac{a_0+a_1+\cdots+a_n}n\leq a_{n+1}.\]
Let \(n\geq 2\) be an integer. Consider an \(n\times n\) chessboard consisting of \(n^2\) unit squares. A configuration of \(n\) rooks on this board is peaceful if every row and every column contains exactly one rook. Find the greatest positive integer \(k\) such that, for each peaceful configuration of \(n\) rooks, there is a \(k\times k\) square which does not contain a rook on any of its \(k^2\) unit squares.
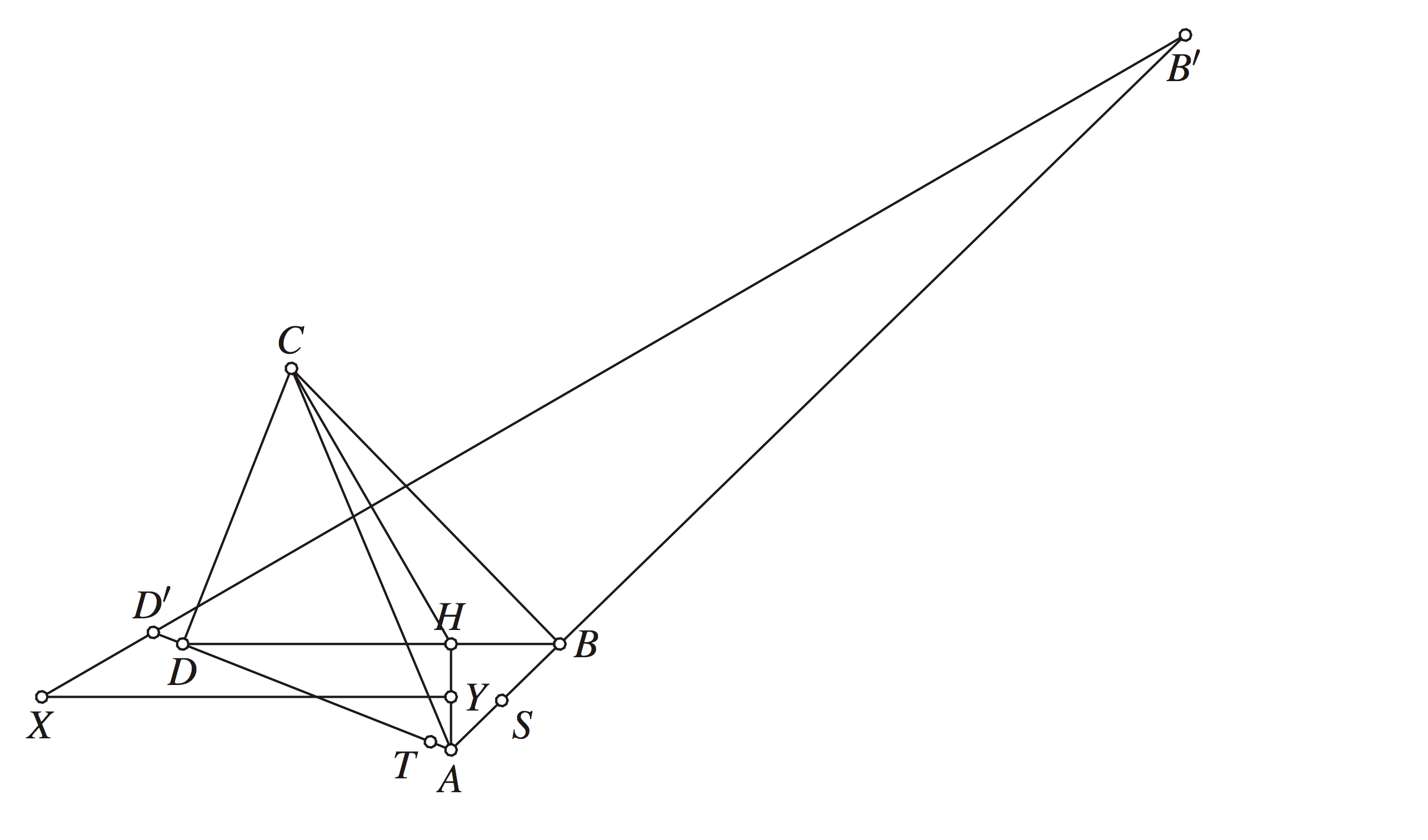
Convex quadrilateral \(ABCD\) has \(\angle ABC=\angle CDA=90^{\circ}\). Point \(H\) is the foot of the perpendicular from \(A\) to \(BD\). Points \(S\) and \(T\) lie on sides \(AB\) and \(AD\), respectively, such that \(H\) lies inside triangle \(SCT\) and \[\angle CHS-\angle CSB=90^{\circ}, \quad\quad \angle THC-\angle DTC=90^{\circ}.\] Prove that line \(BD\) is tangent to the circumcircle of triangle \(TSH\).
Day 2 (July 9, 2014)
Points \(P\) and \(Q\) lie on side \(BC\) of acute-angled triangle \(ABC\) such that \(\angle PAB=\angle BCA\) and \(\angle CAQ=\angle ABC\). Points \(M\) and \(N\) lie on lines \(AP\) and \(AQ\), respectively, such that \(P\) is the midpoint of \(AM\), and \(Q\) is the midpoint of \(AN\). Prove that lines \(BM\) and \(CN\) intersect on the circumcircle of triangle \(ABC\).
For each positive integer \(n\), the Bank of Cape Town issues coins of denominations \(\frac1n\). Given a finite collection of such coins (of not necessarily different denominations) with total value at most \(99+\frac12\), prove that it is possible to split this collection into \(100\) or fewer groups, such that each group has total value at most \(1\).
A set of lines in the plane is in general position if no two are parallel and no three pass through the same point. A set of lines in general position cuts the plane into regions, some of which have finite area; we call these its finite regions. Prove that for all sufficiently large \(n\), in any set of \(n\) lines in general position it is possible to color at least \(\sqrt n\) of the lines blue in such a way that none of its finite regions has a completely blue boundary.
Note: Results with \(\sqrt n\) replaced by \(c\sqrt n\) will be awarded points depending on the value of the constant \(c\).